Users of Microsoft’s flagship 2D-array-based data-organisation tool Excel will be aware of some if its more recondite functions. From the occasionally useful
RIGHT: returns the substring of a given length from the right-hand end of a cell’s contents
to the wilfully obscure
TBILLPRICE: gives “the price per $100 face value for a Treasury bill” when supplied with its settlement date, maturity date and discount rate
to the downright cryptic
N: obviously, converts its argument to a numeric format if it can
along with approximately 340 others, Excel’s abilities are near limitless.
But one function seems singular in the sheer decadence of its inclusion.
Topically. it involves an irrational number which can be approximated as
The number of course is $\pi$, and the function under discussion is SQRTPI. As you might after several tries guess, SQRTPI takes its numerical argument, multiplies it by $\pi$ and returns the square root of this product. That’s certainly a function (on non-negative numbers and taking the principal root anyway). But why has this in particular made it into Excel and not CUBEROOTE or COSINEPHI? Given that the same effect is obtainable using sensible functions with the insertion of three characters, a bespoke function seems somewhat over-the-top. Presumably SQRTPI is used thousands of times daily to justify the negligible per-use saving of its special inclusion?
Excel’s documentation pages are taciturn on the subject, describing only the syntax of the function and no sign of an intended use-case. To Google, then!
Most search results for “SQRTPI” are just republications of the Excel help page, or the equivalent for Google Sheets. But in amongst the documentation chaff is the occasional grain of wheaty discussion. Others, too, have pondered on the enigma of SQRTPI. Among them is a question on Amazon’s ‘askville’ (disappointing; not even Yahoo! Answers) eliciting from user Gary4books the terse and somewhat imperative reply
If you want to calculate what size of a square tank is the same as a round tank you will use this function.
along with a link to a book Excel 2010 In-depth, giving an example of this calculation which the author credits to an anonymous source “from Custom Metalcraft in Springfield Missouri”.
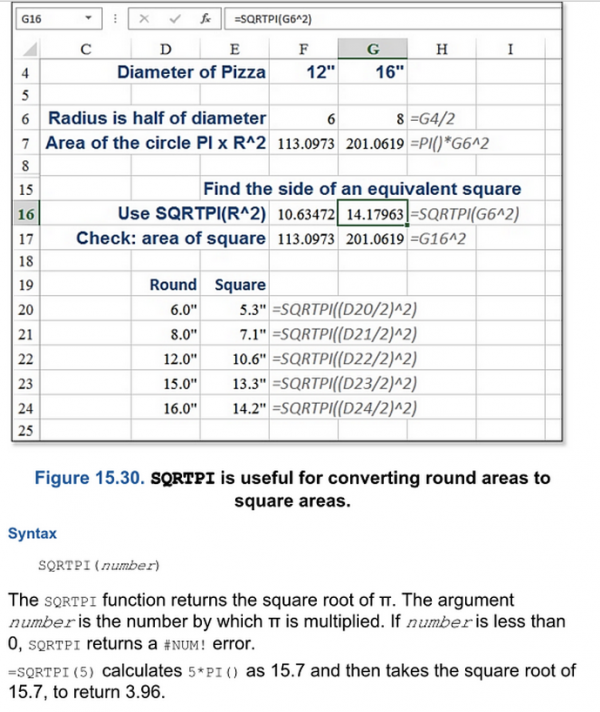
Well, indeed you could fashion a spreadsheet to answer this vexing question using SQRTPI. But since the equation you would be solving is $l^2=\pi r^2$, or $l=\sqrt{\pi r^2}=r\sqrt\pi$, it seems a little optimistic to claim the principal use for this formula is to take a radius and square it before passing it to the function to re-square-root it for you.
Finally to the rescue comes a forum thread at chandoo.org (“Become Awesome In Excel”), with an almost plausible legitimate use for SQRTPI. Picture the scene: you are plotting a histogram of some normally-distributed data and have decided (despite the fact that your chosen statistical package is Excel) to superimpose a bell curve over your data, in an elegant line or perhaps scatter plot. But of course you want the area under your curve normalized to match the area of data being plotted. The area under the standard bell curve is $\sqrt\pi$, so you’ll need to introduce a scaling factor. And why use ten keystrokes for that when six will do? Behold, the SQRTPI-enabled normal distribution curve, with user-editable mean, SD and area.
Let us know if you’ve ever legitimately used SQRTPI, and remember to join us at 13:57:09 on 11/13/15 when we’ll probe the mysteries of DOUBLEFACT.
I stumbled upon this during a discussion of fracture mechanics, in which it is quite common to use sqrt(pi * crack length) in calculations of the force which will cause a crack to grow.