
One of the many jobs we’re gradually getting round to in our new flat is that of tiling a small section of the kitchen surface, which for some reason was left blank by the original builders and all intervening owners. And what better thing to tile it with than binary numbers?
The section of surface in question sits at the right hand end of the counter, which for mysterious reasons doesn’t go all the way to the wall, and a roughly 10cm wide strip of bare wood, lower than the surface, was just asking to be tiled. Mosaic tiles, available from all good DIY shops, can be arranged in any pattern you like, and taking our inspiration from the fact that it would just about fit five 1.5cm-wide tiles across with appropriate spacing, we decided to tile it using black and white tiles to spell out a message in binary. This would suit our existing colour scheme, and be both mathematical and subtle – in that it will pretty much look random to anyone not fluent in ASCII.
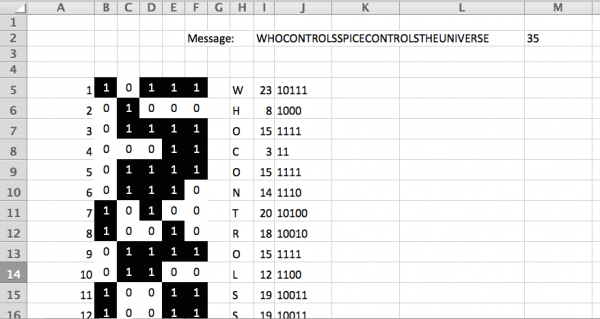
The strip of surface in question was long enough from front to back that we could fit exactly 35 rows of tiles in the other direction, which gave us our message length – each letter of the alphabet could be converted to a number between 1 and 26, which can adequately be expressed using one row of five tiles in binary, meaning we had to come up with a message 35 characters long.
After a lot of discussion, online surveys and soul-searching, we settled on a geeky reference appropriate to the kitchen items usually stored in that area, which is our set of spice racks. From the Dune series of novels by Frank Herbert, the phrase “WHO CONTROLS SPICE CONTROLS THE UNIVERSE” fits perfectly, is not too personally revealing so would be fine if future owners of the property figure it out, and most importantly, looks basically random when spelt out in binary.
Our testing of phrases for this last property was accomplished using a flashy MS Excel spreadsheet, which can be downloaded if you would like one, and thanks to some exceptionally hacky formulae and conditional formatting, will automatically convert a message typed into the box at the top into a pattern of black and white squares for you to play with. This could also be accomplished using e.g. Python, if you’re a proper person, but I use spreadsheets for everything and I don’t care what you think.
The tiling itself was relatively straightforward – we bought a set of black and white square tiles which were already attached to a sheet of webbing, designed to be laid in a checkerboard pattern. We promptly ripped them all off the backing in order to rearrange them into lovely binary. With 3mm spacers in between, the tiles fit snugly in the space, and after some helpful advice from my dad concerning the best type of spreader to use, we soon got them all stuck down in nice straight lines.
The finished tiled surface is (pretty much) level and almost looks like we got a real person in to do it. It also, and this is my favourite part, looks to the untrained eye like any old randomly tiled kitchen counter. The same technique could probably be applied to bathroom walls, splashbacks, the tops of small tables, or anything that usually gets tiled and where it’s not too fiddly to use mosaic tiles.
Here’s a photo gallery of the tiles going on, and the finished product with spice racks back in place. Enjoy!
- Pre-commencement. Tiles laid out for reference
- First few rows going in…
- Almost at the end
- Tiles laid, before final grout layer
- Finished and grouted
- Who controls spice? We do!






Very clever, Stecks, but now I shall be trying to decode every piece of “random” tiling I come across. I may have to mention your name to my psychiatrist…
I bet that’s not the first time a post by Stecks has been the subject of psychiatric discussion.