Christmas wrapping paper is sold in thousands of different variations, including plain, coloured, patterned, foiled and even flock, but one thing it’ll have in common is that it will repeat whatever pattern it has, regularly across the design.
I’m interested in symmetry, and was intrigued to find a curious fact about the symmetries of such repeating patterns – their symmetries are quite limited.
If a shape is finite, like a square, it’ll have a group of symmetries including rotations and reflections; if it’s a hexagon, it might have rotations by multiples of 60 degrees alongside the usual ones, plus some reflections in different axes. Some shapes, like the circle, can be reflected at any angle you like, and still get the same shape back.
When a pattern repeats forever, we can still apply symmetries to it – if the whole pattern has a line of reflection symmetry, we can reflect it; it might also have rotations around certain points, and due to the repeating pattern there’s a new type too, called a glide reflection, which includes a reflection combined with a shift along, so the whole design lines up with the next copy along.
But if you study these symmetries, and work out all the possible ones, it turns out we’re limited to rotations by multiples of 60 and 90 degrees, reflections in axes at the same angles, and glide reflections in those axes. While there’s a little freedom (in whether the axes of different reflections are parallel, and how far apart they are), it’s actually quite a restricted set, and in fact results in only 17 different possible symmetry groups.
Here’s an example of each symmetry group, with an idea of what the symmetries are in each case. Any repeated pattern you find should boil down to one of these options:
- p1: Only translations (no rotations or reflections)
- p2: Four distinct rotations by 180 ̊ but no reflections
- c2mm: reflections and three rotations by 180 ̊, but one of the rotations is not centered on a reflection axis
- cm: Parallel reflections and glide reflections
- p4mm: horizontal, vertical and diagonal reflections, along with two rotations by 90 ̊ and one by 180 ̊.
- p4mg: A rotation of 90 ̊ without a reflection, and a rotation of 180 ̊ with a reflection through it.
- p4: Two rotation centres by 90 ̊, and one by 180 ̊
- pg: Two distinct glide reflections with parallel axes.
- p2mm: Two perpendicular reflections and four distinct families of rotations
- p2mg: Two rotations by 180 ̊ and one independent reflection
- pm: Only reflections with parallel axes
- p2gg: A bit like p2mg, but with a glide reflection instead of a reflection
- p3: Three centres of rotation by 120 ̊ and no reflections.
- p3m1: Three centres of rotation by 120 ̊ and several reflections
- p6: distinct rotations by 60 ̊, 120 ̊ and 180 ̊!
- p6mm: all the rotations of p6, with reflections added everywhere.
- p31m: a rotation by 120 ̊ without a reflection, and another rotation with a reflection.
There’s also an excellent Wikipedia page on Wallpaper groups, with some helpful diagrams that really make sense of it all.
On discovering this, I rushed out to buy a pack of festive wrapping paper. Surely, in a selection pack of multiple designs, I’d find all 17 different combinations? Well, no. Disappointingly, makers of Christmas wrapping paper, along with most people in the world, are less obsessed with symmetry than I am, so they’ve not seen the need to vary the symmetry groups much – and in fact most of the patterns have no symmetries at all beyond the translation symmetry of shifting it across – the trivial symmetry group.
- I call this one ‘Christmas Wordcloud’
- Possibly a nice underlying structure, but that colour scheme? EL NO.
- In this one, Santa looks guilty being caught holding a candy cane. If anyone’s allowed to do that, surely it’s Santa?
- Santa and Reindeer flying planes. Can’t even begin to explain this.
- Not even once.
- No symmetry, but everybody is skating which makes this one my favourite.
Some of the papers I’ve found do have a little symmetry – this one from Aldi (left) has a nice reflection in two different parallel lines, and this deer paper (right) has a few lines of reflection – more if you include the symmetry of inverting the colours, which mostly mathematicians don’t, but I’m struggling here. Everything else was trivial town.
Since I hate disappointment, I’ve played around with some of the designs using photoshop, and I’m sure given enough time and mulled wine I could do the same thing with the actual paper versions, to produce some lovely wrapping paper for gifts (if I’m feeling lazy, I could in theory print my photoshopped versions, but that’s a lot of ink).
 This circles paper has some promise – ignoring the cheesy cartoon Santas, you can swap those out for more of the same symmetrical shapes. I had to nudge the star across a little – since apparently things being in the middle and the right way up isn’t something wrapping paper designers prioritise – to get this version with vertical symmetries (below left); I went really mad and created a hexagonal version (below right), which also has diagonal reflections, since the snowflakes are respectably hexagonal (see Matt Parker’s #snowfake campaign for octagonal snowflake offenders).
This circles paper has some promise – ignoring the cheesy cartoon Santas, you can swap those out for more of the same symmetrical shapes. I had to nudge the star across a little – since apparently things being in the middle and the right way up isn’t something wrapping paper designers prioritise – to get this version with vertical symmetries (below left); I went really mad and created a hexagonal version (below right), which also has diagonal reflections, since the snowflakes are respectably hexagonal (see Matt Parker’s #snowfake campaign for octagonal snowflake offenders).
- This has vertical reflection symmetry in two axes, giving pm symmetry group.
- Check out the diagonal reflections! This one has p3m1 symmetry group.
This red-and-white deers version (below left) lacks the reflections or colour-inversion reflections of the other one, but I did find some nice items in there which could be used to created more symmetrical designs, including this winter flower grid with octagonal symmetry (below right), and these wavy stripes creating vertical reflections in two different ways (below that).
- Original Deers paper
- Four reflections and two centres of rotation! That’s symmetry group p4mm.
- Can you see the difference between this one (pm)…
- and this one (cm)?
I also played around with this gold paper featuring trees (below left) – ignoring the words ‘Merry Christmas’, because who needs that, I’ve tried reflecting half of the tree onto the other half, which sort of looks weird, but gives the whole design a nice vertical reflection line.
- Original paper
- Removed the words
- Tree made using only right half of original tree
- Tree made using only left half of original tree
- Slightly weird looking resulting paper, but it has symmetry group cm.
 If you insist on adding back in the words ‘Merry Christmas’, you could keep the symmetry by using a reflective ambigram, like this one by Scott Kim (right), available printed onto Christmas cards you can buy on Zazzle.
If you insist on adding back in the words ‘Merry Christmas’, you could keep the symmetry by using a reflective ambigram, like this one by Scott Kim (right), available printed onto Christmas cards you can buy on Zazzle.
I was very disappointed by the lack of symmetry groups on display, and it seems to be largely the case wherever you look – although there is hope.
 Mathematician and artist Edmund Harriss, (who we spoke to for the All Squared podcast back in 2013), has come up with a set of 17 designs which each have a different symmetry group! Available on Maths Gear, they’re not specifically Christmassy designs, but have a variety of styles and could be used for either a Christmas gift or any other special gift occasion. Each sheet is labelled with the wallpaper symmetry group it possesses (in Conway’s notation, obvs). A full pack of 17 sheets should surely be enough for all of your Christmas present wrapping needs.
Mathematician and artist Edmund Harriss, (who we spoke to for the All Squared podcast back in 2013), has come up with a set of 17 designs which each have a different symmetry group! Available on Maths Gear, they’re not specifically Christmassy designs, but have a variety of styles and could be used for either a Christmas gift or any other special gift occasion. Each sheet is labelled with the wallpaper symmetry group it possesses (in Conway’s notation, obvs). A full pack of 17 sheets should surely be enough for all of your Christmas present wrapping needs.
Does your Christmas gift wrap have non-trivial symmetry? Send your favourite examples to katie@aperiodical.com and we’ll tweet the best ones from @aperiodical.


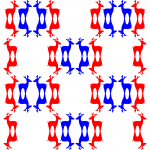

































Nice to see this 17 symmetries done with reindeer! It make it a little more clear about how they’re different.
On the other hand, it makes it tempting to think I can come up with a new combination.
Oh, yeah.. how many combinations are there of x things taken y at a time?
The rules are yet a bit unclear.