
Countdown number-nerd Lovely Rachel Riley has appeared in the latest advert for mobile phone agglomerate EE, alongside massive film node Kevin Bacon.
In the advert, Riley is unable to work out how anyone could not be enticed by the high mobile internet speeds (50% faster, apparently) offered by the company who are paying her to not be able to do so, and this is illustrated by a whole board full of equations and numbers which don’t seem to come to anything. Or do they?
Here at the Aperiodical, we felt compelled to hack apart the maths and see if any of it actually adds up.

It’s difficult to see the whole board at any one time, but by taking and peering at different screenshots we’ve managed to find the following:
- The Rachel Riley-est thing on there is the Countdown-style addition/multiplication in blue near the top of the board, which reads
$$10\ +\ 7\ =\ 17\ \times\ 50\ =\ 850$$This is the kind of running-equations-together-resulting-in-a-completely-nonsense-statement which Riley’s predecessor Carol Vorderman managed to gracefully avoid, but that Riley herself has been seen to illicitly indulge in on occasion. For the record, I feel sick. - Some of the maths on here is quite nice – in the bottom right corner appears to be the equation of a Fourier series:
$$f(x) = \frac{a_0}{2} + \sum_{n=1}^\infty (a_n \cos \frac{n \pi x}{L} + b_n \sin \frac{n \pi x}{L})$$In particular, this is for a function on the interval $(-L,L)$, although whoever wrote it (assuming Rachel, but who knows) has terrible handwriting and their $\pi$s look more like $\sigma$s. 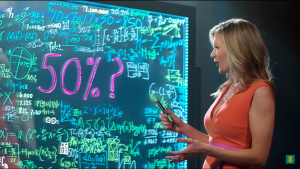 Underneath the large “50%?” (the amount by which the network is claimed to be faster than its competitors) in the centre, there’s a lovely equation about complex numbers:
Underneath the large “50%?” (the amount by which the network is claimed to be faster than its competitors) in the centre, there’s a lovely equation about complex numbers:
$$z’ = x’ + i y’ = |z|e^{i\theta}$$Here, $z’$ is a complex number, and it’s expressed as a sum of real and imaginary parts, then as a modulus/argument (although the angle, denoted $\theta$ here, is missing on the board – where’s it gone, Rachel?) Also, what’s with the dashes? That’s a bit derivative (LOL).- There’s also a bit of a quadratic thing going on in green over to the left of the board, assuming you insert the power of two missing from the first term:
$$ax^2 + bx + c = 0 \\ a \neq 0, \ f(x) = a(x^2 + \frac{b}{a}x + \frac{c}{a})$$This is a way of rewriting the function by dividing through by $a$, which you could do if you’re going on to complete the square – although on the board it’s $“ca”$ (or possibly $“2a”$) where we should have $“\frac{c}{a}”$, so it’s a bit of a swing and a miss.
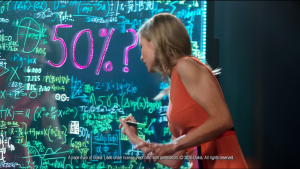 There are probably plenty of other interesting things on there, and as a random board of maths, it’s not too bad – there’s a bunch of numbers and equations about, some of which are actually meaningful. Maths teachers may wish to see how much of it their students can spot, and see if they can correct the errors.
There are probably plenty of other interesting things on there, and as a random board of maths, it’s not too bad – there’s a bunch of numbers and equations about, some of which are actually meaningful. Maths teachers may wish to see how much of it their students can spot, and see if they can correct the errors.
We would like to note that layout-wise, this is terrible use of a board and very poorly structured – we’d like more descriptive notes and ‘implies’ arrows, and if possible a ‘proved it’ square in the bottom right corner. Secretly we’d just like a funky glass board in our house to write maths on.
It’s not clear what mathematical approach Rachel is taking to the question posed, or indeed whether maths will help at all. Riley, who used to work as an analyst for a price comparison website [1], apparently hasn’t considered that maybe this network that’s 50% faster might be charging more, or have worse customer service (or have unbearably smug Americans in their adverts). Also, don’t get us started on what “50% faster” means.
It is good though to see Rachel being used as a stereotypical example of a clever person who should be consulted to answer difficult questions – if not even the mighty power of Rachel Riley doing some maths can solve it, then nobody can. Go maths!
Brief investigations can’t find any published maths papers by RR (happy to be corrected though), meaning despite now having a Bacon number of 1, her Erdős number remains infinite, so her Erdős-Bacon number is still sadly infinity, along with the rest of us. We’ve just invented the concept of Erdős-Bacon Difference, which is the modulus of the difference between your Erdős and Bacon numbers, and surely Rachel’s is now the most it can possibly be for a maths person. So she wins that, even if she wasn’t able to solve Kevin’s real-world problem.
Join us next time when we’ll be attempting to comb all of the hair flat on the weird purple muppet from the Three adverts.
More information
EE Advert, on YouTube (other mobile phone companies are available)