Warning: you could make a very strong argument I’ve thought far too much about something inconsequential. If that makes your stomach turn, look away now.

This morning in the shower, I had an idle thought about my towel. It was, as always, folded neatly on the toilet seat. A problem that’s been bugging me for a few days is how to pick up the towel by a section of the long edge, so when it unfolds it’s the right way round.

The problem is that the short edge and the long edge look the same, and once I’ve folded the towel over a couple of times and had a shower only a madman* would remember which is which. But my towel isn’t square, so it occurred to me that either the longer or the shorter edge, after folding, could be the edge I want. Since I never make a diagonal fold, the long edge is only ever folded on top of the long edge, and likewise for the short edge. I fold the towel until it fits comfortably on top of the toilet seat, and by the time I’ve finished my shower I can’t be relied upon to remember which sequence of folds I did.

Which got me thinking about the ratio between the width and height of my towel: if I know this ratio then, by looking at the towel and counting the number of folds, I can work out which folds I’ve done, and hence which of the sides will unfold to be the long edge.

So let’s call the longer edge $w$, and the shorter edge $h$. Because my towel is both hard to fold and doesn’t show up well in photographs, I’ll use a sheet of A4 paper to show you how the method works.

The method

First I set a handy marker for the shorter length, $h$, to compare against. Ideally I’d do this comparison by eye, but once the two measurements start getting close to each other it’s hard to tell. Another way to tell which is bigger would be to do a temporary diagonal fold in the paper, putting the two lengths directly on top of each other.

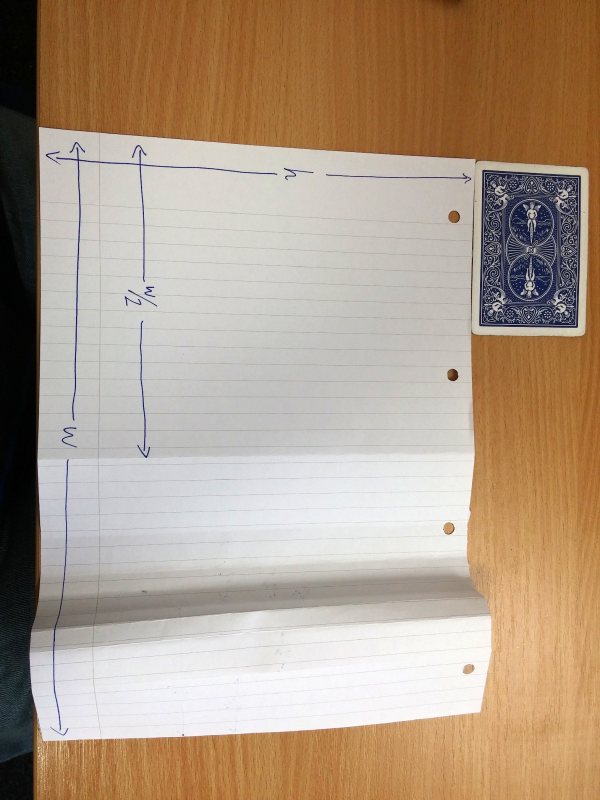
Then, I show that $w \gt h$.

So I fold the paper in half, and see that $\frac{w}{2} \lt h$.

To get a known length between $\frac{w}{2}$ and $w$, I unfold the paper and make a new fold in the right half, giving me a width of $w \left(\frac{1}{2} + \frac{1}{4} \right) = \frac{3}{4}w$. You can see that $\frac{3}{4}w \gt h$.

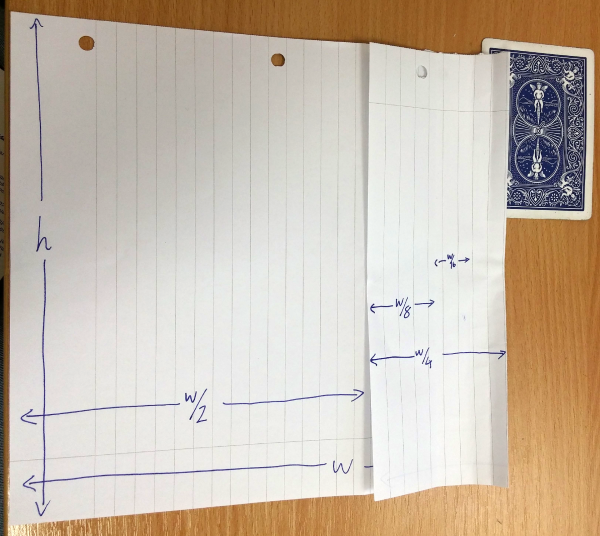
So I fold that quarter in half to get a width of $w \left(\frac{1}{2} + \frac{1}{8} \right) = \frac{5}{8}w \lt h$.

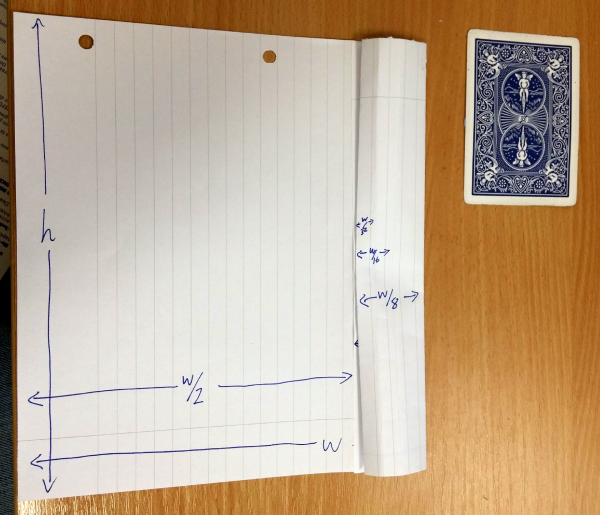
Again, to get a bigger width I unfold the last fold and make a new fold in the right portion, giving me $w \left(\frac{1}{2} + \frac{1}{8} + \frac{1}{16} \right) = \frac{11}{16}w \lt h$.

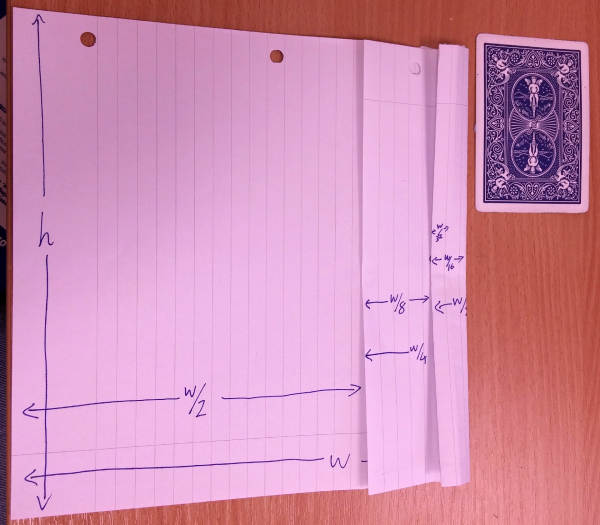
One last step gives me $w \left(\frac{1}{2} + \frac{1}{8} + \frac{1}{16} + \frac{1}{32} \right) = \frac{23}{32}w \gt h$.

At this point, I had reached the limits of my ability to accurately fold very thin strips of paper, so I stopped. The last measurement to the left of the marker I had was $\frac{11}{16}w$, and the last one to the right was $\frac{23}{32}w$. So I’ve got upper and lower bounds for $h$:

\[ \frac{11}{16}w \lt h \lt \frac{23}{32}w \]

My best bet for the real value of $h$ is the midpoint of my two bounds, so $h \approx \frac{45}{64}w$, or $\frac{w}{h} \approx \frac{64}{45} = 1.4\dot{2}$. That’s pretty darn close to $\sqrt{2} = 1.414…$! If I didn’t already know that every sheet of A4 is a silver rectangle, this would be enough for me to make a good guess.

Why it works

The method I used is a binary search: at each step, I changed my estimate by half as much as I did in the previous step. If the resulting measurement was less than $h$, I added that amount to my approximation. So, the calculation went like this:

\begin{align}
w &\gt h & &✗\\[0.5em]
\frac{1}{2}w &\lt h & &+\frac{1}{2} \\[0.5em]
\frac{3}{4}w &\gt h & &✗ \\[0.5em]
\frac{5}{8}w &\lt h & &+\frac{1}{8} \\[0.5em]
\frac{11}{16}w &\lt h & &+\frac{1}{16} \\[0.5em]
\frac{23}{32}w &\gt h & &✗
\end{align}

That’s much more concisely written in binary as $\frac{h}{w} \gt 0.10110_2$. And because the last measurement was bigger than $h$, I know that $\frac{h}{w} \lt 0.10111_2$.

This method works for any ratio, not just $\sqrt{2}$ – it’ll produce lower and upper bounds, in binary, for the true value of the ratio. And if the ratio is a dyadic rational – a fraction of the form $\frac{a}{2^b}$ – you’ll eventually get a measurement that lines up exactly and the process will terminate!

If I was just trying to get an approximation for $\sqrt{2}$, obviously this paper-folding method isn’t the best – apart from anything else, A4 paper is defined as 297mm by 210mm, which could only ever give me four decimal places of $\sqrt{2}$. However, this binary search method to find $1/\sqrt{2}$ works in algebra too:

\begin{align}
1^2 &\gt \frac{1}{2} & & ✗\\[0.5em]
\left(\frac{1}{2}\right)^2 = \frac{1}{4} &\lt \frac{1}{2} & &+\frac{1}{2} \\[0.5em]
\left(\frac{3}{4}\right)^2 = \frac{9}{16} & \gt \frac{1}{2} & &✗\\[0.5em]
\left(\frac{5}{8}\right)^2 = \frac{25}{64} & \lt \frac{1}{2} & &+\frac{1}{8} \\[0.5em]
\left(\frac{11}{16}\right)^2 = \frac{121}{256} & \lt \frac{1}{2} & &+\frac{1}{16} \\[0.5em]
\vdots
\end{align}

Here, I’ve used the fact that $\frac{a}{b} \lt \sqrt{2}$ if $a^2 \lt 2b^2$ to easily decide what to do at each step. Because we’re now working purely in algebra, we can keep going forever.

As for my towel, the folding method tells me that its aspect ratio is bang on 11:16. Or, more likely, it’s 2:3 and I made a measurement error. $\frac{2}{3}$ isn’t a dyadic number, after all.