In this series of posts, Katie investigates simple mathematical concepts using the Google Sheets spreadsheet app on her phone. If you have a simple maths trick, pattern or concept you’d like to see illustrated in this series, please get in touch.

Having spoken at the MathsJam annual conference in November 2016 about my previous phone spreadsheet on multiples of nine, I was contacted by a member of the audience with another interesting number fact they’d used a phone spreadsheet to investigate: my use of =MID() to pick out individual digits had inspired them, and I thought I’d share it here in another of these columns (LOL spreadsheet jokes).

Twin primes, which are pairs of prime numbers with a difference of two, are well-studied. It’s not known whether there are infinitely many such pairs (although we’ve made some progress on that), but it’s suspected. The gaps between pairs get larger as you go up the number line, and there’s a few interesting bits known about them, including Brun’s Theorem. Today I’m going to investigate a thing about their products.

We can start by populating a spreadsheet with a list of pairs of twin primes, starting with the classic \((3,\!5)\) and proceeding from there. This data was obtained from the amazing resource at primes.utm.edu, maintained by known prime-basher Chris Caldwell. Putting this list of primes in the first column, and populating the second column with the number two higher gives us a lovely list of twin prime pairs.

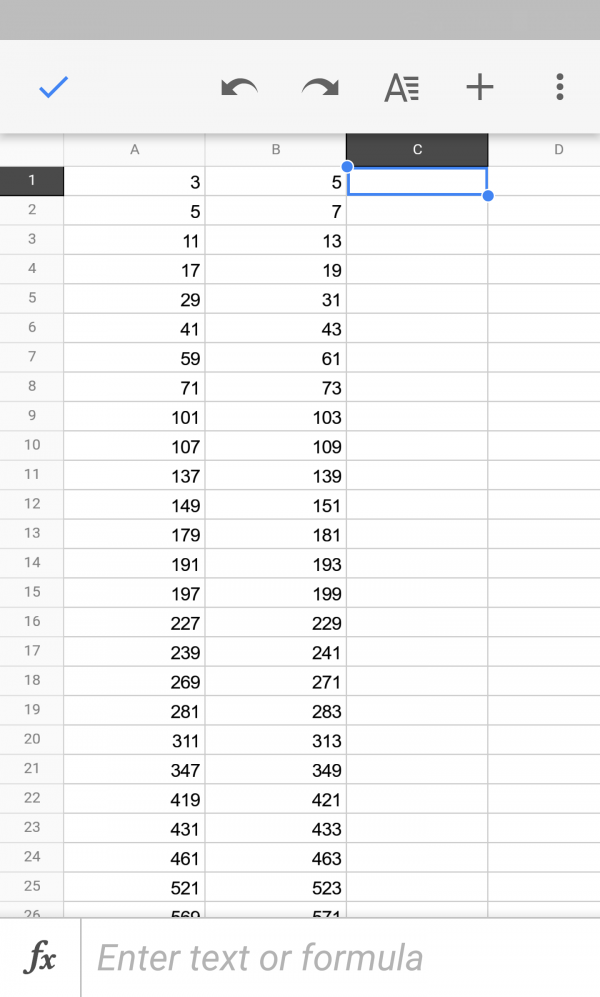
In the next column, we calculate the product of each pair:

And in the fourth column, we can use a similar MID() / VALUE() based construction to find the sum of the digits in this number:

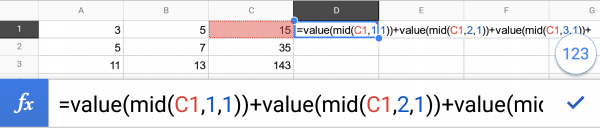
Giving the not-especially-interesting result:

Or is it? In the fifth column, we can take =MOD(this value,9) and see what happens:

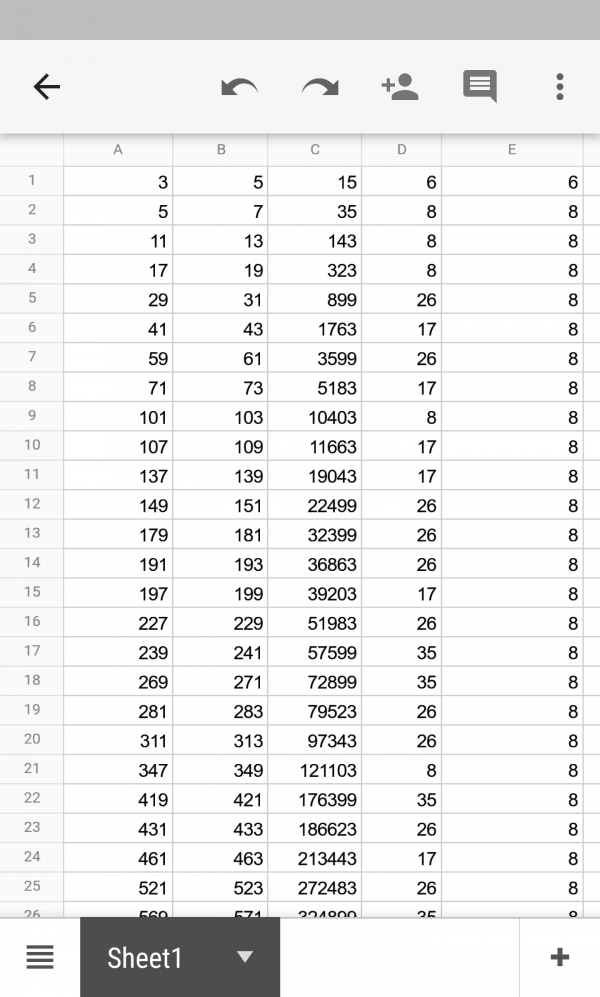
With the exception of the first row, and let’s be honest the first one’s always weird anyway, you’ll see that all of these numbers have the value $8$ modulo $9$.

INTERESTING!

For an explanation of this, done in a bar after a few pints of course, we can thank sometime Aperiodical contributor and general maths guy Colin Beveridge, who contributes the following; if you’d like to try and work it out yourself, we’ve made these bullet points appear one at a time when you click, so you can use as many as you need and work the rest out.

• All twin prime pairs other than $(3,5)$ are of the form $6n +1$ and $6n – 1$ (it says it on Wikipedia so it must be true; left as a pleasing exercise for the reader)
• The product will therefore be of the form $36n^2 – 1$ (classic difference of two squares)
• This means the first part of this number will be divisible by $9$, as $36$ is divisible by $9$
• The whole thing must therefore be congruent to $8$ modulo $9$, as it’s a multiple of $9$ minus one.
• This means the sum of the digits of the number will also be $8$ modulo $9$.

A fun diversion for everyone. Thanks to Simon Allen, who sent me the email, and to Colin for his neat explanation, relayed via Simon.

If you’ve seen any nice number facts I can investigate using a spreadsheet on my phone, please send them in!