This is a guest post by researcher Audace Dossou-Olory of Stellenbosch University, South Africa.

Consider the following question: How many ways are there to connect $2n$ points on a circle so that each point is connected to exactly one other point?

Circular reasoning

For example, for $n=2$ there are four points on the circle – say, $P_1,P_2,P_3,P_4$ arrange clockwise. If $P_1$ is mapped to $P_2$, then $P_3$ can only be mapped to $P_4$. Likewise, if $P_1$ is sent to $P_4$, then $P_3$ can only be sent to $P_2$. If $P_1$ and $P_3$ are connected, then mapping $P_2$ to $P_4$ creates an intersection point.

This shows that for $n=2$, the answer is $2$.

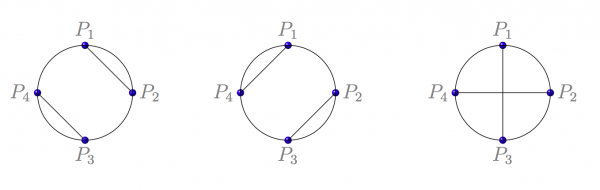
Figure 1: Illustration for n = 2

What is the answer to this question for general $n$? For $n=3$, the answer turns out to be $5$.

The problem can be solved by setting a recurrence relation: denote by $C_n$ the number of ways to connect $2n$ points $P_1,P_2,\dots ,P_{2n}$ on a circle so that each point is connected to exactly one other point.

For $n=0$, there is nothing to do, and so $C_0=1$. Assume $P_1$ is mapped to $P_k$ for some $k=2,3,\dots ,2n$. Then, none of the points $P_2,\dots ,P_{k-1}$ can be mapped to one of the points $P_{k+1},\dots ,P_{2n}$ because this will create an intersection point. Furthermore, $k$ must be an even number, otherwise one of the points $P_2,\dots ,P_{k-1}$ will be left out.

Therefore, we have $$\begin{array}{r}{C}_n=C_0\cdot C_{n-1}+C_1\cdot C_{n-2}+\cdots +C_{n-2}\cdot C_1+C_{n-1}\cdot C_0\\ =\sum _{j=0}^{n-1}{C}_j\cdot C_{n-1-j}.\end{array}$$ ‘Solving’ this non-linear recursion leads to the formula $$\frac{1}{n+1}(\genfrac{}{}{0ex}{}{2n}{n})$$ For $n\ge 1$, the sequence starts $1,2,5,14,42,\dots$ $C_n$ is called the $n$^th Catalan number.

These numbers were introduced by the French and Belgian mathematician Eugène Charles Catalan. As it turns out, Catalan numbers count various combinatorial structures such as the ‘number of trees’.

What is a tree?

A tree is a graph that satisfies the following conditions:

• two nodes can only be connected through one edge (no multiple edges between pairwise nodes);
• no loop at a node (no node can be connected to itself via an arc);
• the edges of the graph are not oriented – they are simple edges;
• there is always a path to get from one node to another (the graph is connected);
• there is no cycle (a path that starts and ends at a same node) in the graph.

In other words, a mathematical tree is a graph in which any two nodes are connected by a unique path.

But how many trees are there? Mathematicians and computer scientists had already started answering this question since the work of the German mathematician Carl Wilhelm Borchardt in 1860, before the work of Cayley, Pólya, Prüfer and many others.

Nowadays, the study of trees involves determining a vast number of properties, such as the number of possible trees given a number of nodes.

We highlight three types of trees that are counted via Catalan numbers.

If we choose one node of the tree and call it the root, we have what is called a rooted tree. Thinking of the root of a tree as a common ancestor to all other nodes in the tree, we define the notion of a successor – a node further along the same path in the tree. $C_n$ enumerates:

The number of binary trees with $2n+1$ nodes

A binary tree is a rooted tree in which each node has two successors or no successor at all; the number of possible such trees with $2n+1$ nodes is the $n$^th Catalan number.

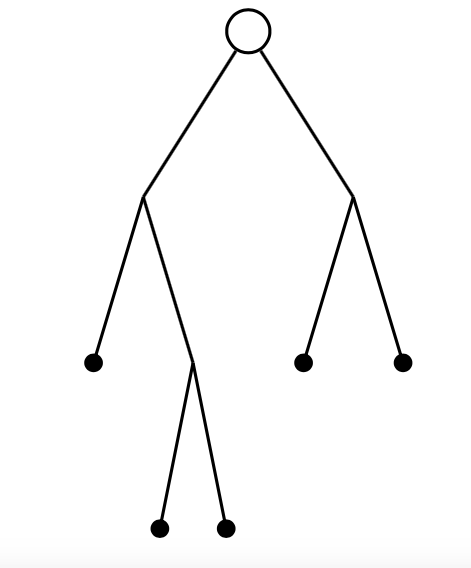
Figure 1: A binary tree with 9 nodes

The number of pruned binary trees with $n$ nodes

A pruned binary tree is a rooted tree obtained from a binary tree by leaving out all nodes with no successors; the number of possible such trees with $n$ nodes is the $n$^th Catalan number.

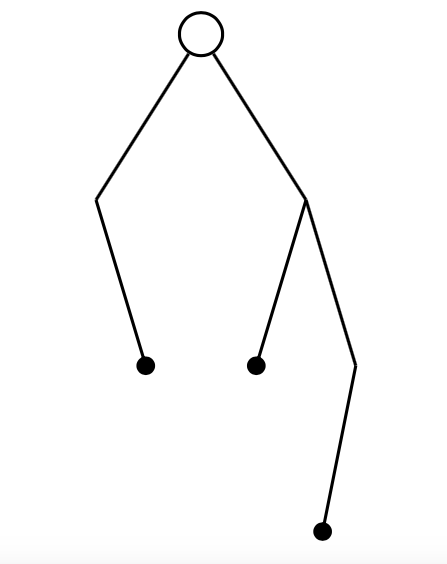
Figure 2: A pruned binary tree with 7 nodes

The number of plane trees with $n+1$ nodes

A plane tree is a rooted tree in which a node can have any number of ordered successors; the number of possible such trees with $n+1$ nodes is the $n$^th Catalan number.

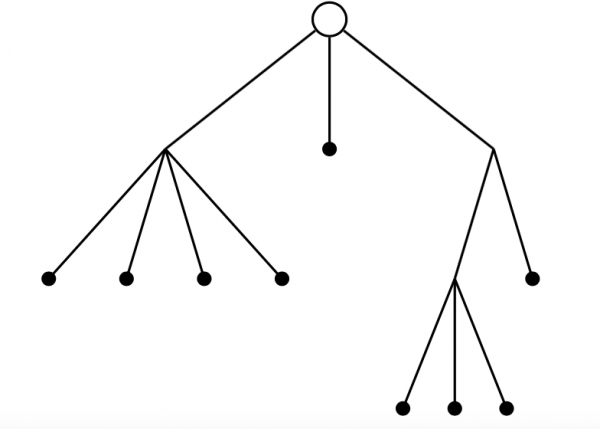
Figure 3: A plane tree with 13 nodes

Further uses of Catalan Numbers

Besides trees, amongst other structures counted by $C_n$, we have the number of Dyck paths of length $2n$. A Dyck path is made from ↗ and ↘ unit-length steps in the $xy$-plane that start and end on the $x$-axis but never go below it.

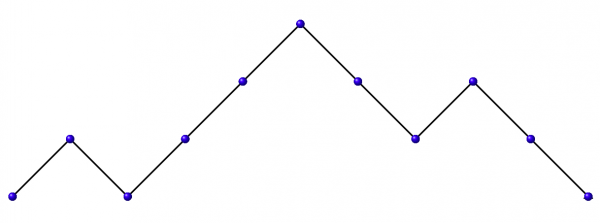
Figure 4: A Dyck path of length 10

Also, (and just for fun), you could try to compute the following integral: $$\frac{2^{1+2n}}{\pi }{\int }_{-1}^1{x}^{2n}(1-x^2{)}^{1/2}\mathrm{d}x$$ You would find the answer is… the Catalan numbers again!

If you’d like to write about some maths that you find interesting, get in touch!