This week, Katie and Paul are blogging from the Heidelberg Laureate Forum – a week-long maths conference where current young researchers in maths and computer science can meet and hear talks by top-level prize-winning researchers. For more information about the HLF, visit the Heidelberg Laureate Forum website.

The HLF included a talk from 2018 Fields medalist Caucher Birkar. His subject area, algebraic geometry, is one of the largest fields of research within pure mathematics (over a quarter of the 60 Fields medals awarded since 1936 have been to people working in algebraic geometry), and it has connections to many other fields of maths including topology, algebra and number theory. But what exactly is algebraic geometry? Well, if you’ve studied maths at school, there’s a pretty good chance you’ve already done some.

What is Algebraic Geometry?

Algebraic geometry considers spaces of polynomials – equations which use one or more variables raised to powers. A simple example might be:

$x^3 + 3x^2 – 4x + 5 = 0$

Each of the terms in the polynomial has a coefficient in front of it, which can be 1 (in which case it’s not written), and can be 0 (in which case that term doesn’t appear) or can be another number. Depending on what kind of polynomial you’re working with (more strictly, over which field you’re defining your space of polynomials), you might use whole numbers, fractions or even complex numbers in front of each term. In our example above, there’s an $x^3$ term, an $x^2$ term, an $x$ term (which in this case has a negative coefficient) and a constant term.

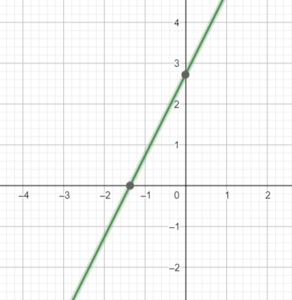
This kind of polynomial equation (poly = many, nomos = part; a thing with many parts) can be used to describe all kinds of systems and objects. Simple example polynomials might not have terms with high powers – for example, a polynomial with just an $x$ term and a constant term is called linear, so-called because it describes a straight line if you draw it on a graph.

This line represents all the points for which $y = 2x + 3$: at $x = 0, y = 3$ and at $x = 1, y = 5$ as you would expect. Many of you will be familiar with this kind of graphical representation of an equation, and might have also seen what happens to the graph of a polynomial as you include higher powers as terms.

A graph with a squared term (left) is a quadratic, and will have a u-shaped (or n-shaped, depending on whether the $x^2$ term has a positive or negative coefficient) curve. A cubic polynomial (centre) will usually have a wiggle in the middle, but will have the ends going in opposite directions, and a polynomial with an $x^4$term (a quartic, right) will look like a quadratic but with an extra bump. The more terms, the more bumps you can get.

But is it geometry?

Some of you may be wondering why this area of research is known as Algebraic Geometry – the algebra is clearly there, in the form of equations – but where’s the geometry?

Well, there are two problems here. Firstly, the type of algebra referred to in the name isn’t the kind of algebra you’ll remember from school, where you do the same thing to both sides of an equation and move terms around to get the answer. At university and research level, algebra is the branch of pure maths concerned with structures like groups and fields. Such objects are abstractly defined, and are essentially sets with rules. The set of all real numbers forms a field, because it’s a collection of things (numbers) you can combine together using addition and multiplication, and if you do this you always get another thing that lives in the same field (a number). There are a few other conditions to specify the different types of objects – called groups, rings, fields, and even algebras, and these can be used to describe real objects or structures – the group associated with moves on the Rubik’s cube being a nice example.

So algebraic geometry involves considering not just individual polynomials, but the ring of all possible polynomials, given the variables you’re putting in (sometimes just $x$, or sometimes a whole set of variables, usually labelled something like $x_1, x_2\ldots x_n$) and the field you’re using to pick coefficients (such as the real numbers, the set of all fractions, or the complex numbers).

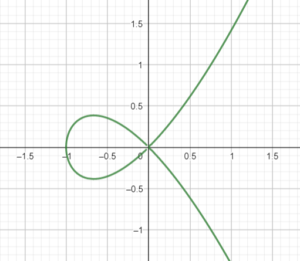
The geometry aspect is slightly less obvious – but it has actually already started making itself apparent. By defining the linear polynomial $y = 2x + 3$, we’ve already seen how this corresponds to an object on a 2D graph. If your polynomial has more than one variable, this shape will exist in more than 2 dimensions. Each polynomial defines an object in space – a line, a plane or a solid, or anything else, and by studying the polynomials you can examine the geometry of these shapes and the connections between the abstract numerical object and the slightly more tangible (at least in lower dimensions) shapes. Algebraic curves (shapes defined by polynomials) range from simple lines and circles to beautiful complicated shapes with exciting names like the cycloid, the quadrifolium and the Conchoid of Nicomedes.

Birkar’s work in algebraic geometry concerns the structures you can construct from the rings of polynomials, how these generalise to higher dimensions, and how to deal with singularities in the space (points where the polynomial doesn’t look like a simple curve). His Fields medal was awarded for work on morphisms, maps used to ‘patch’ varieties (collections of polynomials) at points where they have singularities, so that they can be studied more easily.

Algebraic geometry connects to the study of shapes in topology, the use of polynomials to model mathematical problems, and it has connections to cryptography through the polynomials used in encryption, and to higher level physics concepts such as string theory. Since you’ve certainly already done a very small amount yourself – whenever you’ve sketched a graph of $x^2$ – you can maybe appreciate the importance of Birkar’s achievement and the beauty of this kind of mathematics, even if you’re not quite at Fields medal level yet.