 This week, Katie and Paul are blogging from the Heidelberg Laureate Forum – a week-long maths conference where current young researchers in maths and computer science can meet and hear talks by top-level prize-winning researchers. For more information about the HLF, visit the Heidelberg Laureate Forum website.
This week, Katie and Paul are blogging from the Heidelberg Laureate Forum – a week-long maths conference where current young researchers in maths and computer science can meet and hear talks by top-level prize-winning researchers. For more information about the HLF, visit the Heidelberg Laureate Forum website.
Alongside the HLF this year, an exhibit celebrates female mathematicians from around Europe (written about by Gina in a post earlier this week) and includes photographs, interview quotes and beautiful mathematical equations, which come together to create an illuminating and at times poetic snapshot of the life and work of a mathematician.
The equations in particular caught my eye, each splashed across the poster in a different bright colour. They’re used more as an illustration of the type of maths each person works on, rather than giving any mathematical background – but I was intrigued, and thought I’d investigate a few of them, and share some of the mathematics represented.
 Subject area: Cluster algebras, cluster categories, representation theory, categorification
Subject area: Cluster algebras, cluster categories, representation theory, categorification
Karin’s work involves algebras – structures defined using a basic collection of objects, with an underlying set of numbers used to scale them. An example might be the complex numbers, discussed in the post on the Riemann Hypothesis, in which the objects are just the number i, and the underlying set is the real numbers. You can combine multiples of $i$ with real numbers, to get complex numbers of the form $a + ib$, and these can be combined by addition, or multiplication to give other complex numbers. Some algebras have more than one object that can be combined in different multiplicities – for example, the quaternion numbers are defined in a similar way but using $i, j$ and $k$ – each of which can be multiplied by scalars, but also interact with each other in specified ways (in this case, $i^2 = j^2 = k^2 = ijk = -1$). In particular, Baur’s work is on Cluster Algebras, whose collection of objects is generated from a seed set using particular rules.
The equation relates A, an algebra, to EndB, which is a collection of endomorphisms. Endomorphisms are maps from a particular object to itself – for example, given the set of numbers {1, 2, 3} you could consider all the maps taking this set to itself, by reordering the numbers:
{1, 2, 3} → {1, 2, 3}
{1, 2, 3} → {1, 3, 2}
{1, 2, 3} → {2, 1, 3}
{1, 2, 3} → {2, 3, 1}
{1, 2, 3} → {3, 1, 2}
{1, 2, 3} → {3, 2, 1}
Once you have defined the endomorphisms of an object, they can then be considered as a structure in themselves. In the same way as with the objects in the algebra, you can combine one endomorphism with another to get a different one:
e.g. {1, 2, 3} → {1, 3, 2} combined with {1, 2, 3} → {2, 1, 3}
This would swap the second and third elements, then swap the first and second elements, giving the result {1, 2, 3} → {3, 1, 2}. Studying all the possible endomorphisms of a given algebraic object tells you something about its structure, and the collection of endomorphisms can also form an object to be studied.
The equation is from Karin’s paper “Dimer Models and Cluster Categories of Grassmannians”, with Alastair King and Robert J. Marsh. In this paper, they show that the particular algebra they are studying, A, is isomorphic to (the same as) a particular endomorphism algebra, giving them a better understanding of its structure.
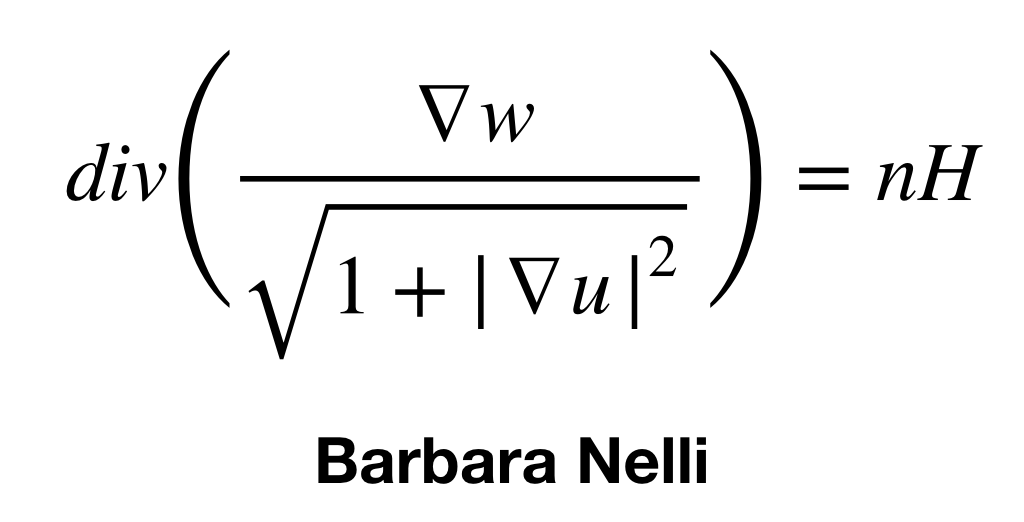
Subject area: Geometric analysis, minimal surfaces, Dirichlet problem, geometric maximum principle
This equation is from Nelli’s paper, Minimal surfaces in $\mathbb{H}^2 \times \mathbb{R}$, written with Harold Rosenberg, in which they prove various results about the space $\mathbb{H}^2 \times \mathbb{R}$.
$\mathbb{H}^2$ here represents the hyperbolic plane – a surface in which the space curves away from itself at every point. This sounds confusing, but it’s difficult to picture as it doesn’t fit in our normal 3D universe. Compared to our usual geometry (called Euclidean geometry), it has major differences. One of the fundamental ideas in geometry is if you have a point near a line, there’s only one line that passes through that point and is parallel to the original line – this is known as Playfair’s axiom. In hyperbolic space, there can be more than one such line – all of which pass through the same point, but don’t intersect each other, or cross the original line, anywhere else. This is because of the way the space is curved, and it’s a fundamental property of so-called Hyperbolic geometry.
Poincaré Disc, with (6,4,2) triangular hyperbolic tiling – the triangles are all the same size and shape
Hyperbolic space can be visualised using the Poincaré Disc – a circle in which distance behaves strangely near the edges. Distances in the centre of the disc behave just as normal in the regular 2D space we’re used to, but as you get nearer the edges, distances get shorter – until, on the boundary of the disc, points which look close together are actually far apart, and straight lines become curved.
A nice way to think about it is to imagine you’re creating a circular piece of crochet, but each line of stitches as you go further out from the centre has more stitches in it. Such a crochet piece might start off flat, but as you get further out it’ll need to ripple up and down to accommodate the extra stitches – but in the hyperbolic plane, this extra surface is just squashed in to the same space, and the definition of distance is difference there.
The space$\mathbb{H}^2 \times \mathbb{R}$ represents the result of taking the direct product of the hyperbolic plane with the real line $\mathbb{R}$. Direct products are analogous to putting two things at right angles – for example, the direct product of a circle and the infinite real line $\mathbb{R}$ is an infinite cylinder, and the direct product of two real lines $(\mathbb{R}$ \times\mathbb{R})$ is $\mathbb{R}^2$, the 2-dimensional real plane.
Nelli’s work here concerns the Dirichlet Problem, which involves solving differential equations, and this equation describes the divergence (a property of the related vector field) of a function defined on $\mathbb{H}$^n, n-dimensional hyperbolic space.
 Subject area: Algebraic groups and Lie algebras, Poisson structures, harmonic analysis on Gelfand pairs
Subject area: Algebraic groups and Lie algebras, Poisson structures, harmonic analysis on Gelfand pairs
This equation is known as Weyl’s character formula, and it’s from a branch of maths called representation theory, which is connected to the idea of groups – collections of objects, much like algebras, but without the underlying set of scalars. Group theory is concerned with how the objects making up the group behave when combined in different ways, and group structures often underlie other mathematical ideas – the group describing all possible moves on a Rubik’s cube is a nice example.
Representation theory involves representing elements of a group or other algebraic structure in terms of linear transformations of vector spaces. Results from this common ground can then be used to learn about the original structures. Representation theory often pops up in other areas of research, as the underlying groups the structures are based on show the connections between different areas.
As with numbers and primes, representations can be ‘broken down’ into products of smaller representations (transformations of spaces with fewer dimensions). Those representations which cannot be broken down are called irreducible representations. Much like prime numbers, properties of irreducible representations are particularly important.
The character of a representation condenses this further, assigning to elements of the group a single ‘number’ which captures much of the information in the representation. Weyl’s character formula gives information on the characters of the irreducible representations of a certain type of group, known as a compact Lie group. Lie groups, which Oksana works with, are groups that can also be considered as topological shapes.

One Response to “HLF Blogs: Equations of Women in Mathematics”