Inspired by Katherine Johnson’s character in the film Hidden Figures and her use of Euler’s Method, engineer Natalie-Claire Luwisha has written this guest post about Euler’s contribution to engineering.

I thoroughly enjoyed Hidden Figures because of the overall message and inspiration it generated for all women, especially women of colour. Even today in the 21st century, most of the STEM (science, technology, engineering and mathematics) industries still have a very low percentage of women and even fewer women of colour. One major factor in this is the lack of visible role models for young girls and women to aspire to, so this story based on real-life events was ideal to help tackle the issue.

The film highlighted the struggles and triumphs that the three African-American women went through during their time at NASA, where their intelligence contributed to putting a man into space.

Euler’s Method in Hidden Figures

This was a film in which mathematicians were the central characters, and I was pleased to note that they didn’t shy away from including real mathematical methods in the script. Explicitly mentioned in the film is Euler’s method, used to find an exact solution for a differential equation. In the film, the method is used to find a solution between two different types of orbit that the capsule moves during its journey from space to earth.

Although the method is described as ‘old math’ in the film, many engineers and mathematicians frequently use it in their work today. Euler’s method was first published in 1768, and the movie is set in 1960 – this is hardly a long time in comparison to some of the methods we use in many of our mathematical calculations today, such as Newton’s laws.

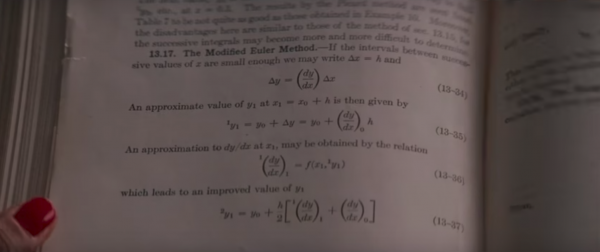
A still from the film, in which Katherine Johnson looks the method up in a textbook

Below is the scene in which it’s used:

Who’s this Euler?

The method is named after Leonhard Euler, a mathematician who was born in Switzerland in 1707. Although he is famously known as a great mathematician he was a highly intelligent individual who contributed to other STEM areas including physics, astronomy, and engineering.

During his childhood, his interest in maths was influenced and supported by his father’s friend, Johann Bernoulli, who at the time was the most renowned mathematician in Europe. Euler spent most of his adult life in Russia and Germany (previously known as Prussia).

At the age of 13, he attended the University of Basel and achieved a master of philosophy where his dissertation focused on the philosophies of Descartes vs Newton. While studying at university, Bernoulli mentored and tutored Euler, thus cultivating his natural talent in mathematics. Although Euler’s father had wanted him to focus more on his theology studies, it was Bernoulli who convinced his father of the phenomenal talent his son had in mathematics.

In his lifetime Euler made various historical developments in physics, astronomy, and engineering. Today we have numerous examples of his work, especially in mathematics. Thus we find ourselves with a number of topics and formulas that are part of (derive from) Euler’s work. Some of the mathematical areas that Euler contributed to include:

• Euler Characteristic in topology
• Mathematical notation, such as that used for functions: f(x)
• Analysis in calculus and algebra
• Euler’s totient function in  number theory
• Graph theory
• Logic
• Applied mathematics

Even the Euler Brick which has been written about here on the Aperiodical before now! Euler also used his analytical skills to help develop many engineering formulas. 

As an engineer myself, I use various mathematical methods in structural engineering analysis, and one of them is also named after Euler.

Euler’s Column Formula for Buckling

Euler’s Column Formula is based on the theory of bending, as applied to structural beams and other structural members under different stresses. By solving the differential equation of beam bending we are then able to find an exact solution for the lateral (sideways) displacement of a column at its critical load – that is, the maximum load it can take in the axial (vertical) direction before it bends.

(Images above are from the Cal Poly website, and the FSEL website.)

This displacement, also described as buckling, is the physical failure i.e. – bending or deformation of a column, due to compressive stresses (axial load) higher than its critical load. Many examples of this type of failure can be found in buildings made of steel or concrete columns that buckle, cylindrical storage tanks and even drink or food cans, can have signs of buckling.  

The basic formula used is:

\[ P= \frac{\pi^2 E I}{L^2} \]

Where $P$ is the critical buckling load, $E$ is Young’s modulus of elasticity, $I$ is the second moment of area and $L$ is the effective length of the beam – the exact value used for $L$ varies depending on the type of connection between the column and the structure. The different types of connections are shown in the diagram below, and the effective length of the column is then dependent on these end conditions.

As shown above, the effective lengths for the different types are as follows (where L is the actual length of the beam and $L_{eff}$ is the effective length.

• Pinned connection at both ends: $L$
• Fixed connection at both ends: $0.5L$
• Fixed and pinned connection: $0.699L$
• Fixed at one end only or cantilevered: $2L$
• Fixed at one end and fixed in one direction – roller on the other end: $L$

Where does this formula come from?

This formula is derived from the beam bending equation:

\[ EIy”=M \]

This produces the differential equation:

\[ EIy”+ P = 0 \]

Where $P$ represents the compressive load on a column.

By identifying the critical buckling load of a column, we can design the column to withstand up to 70% of this load and ensure the stability of the structure, hence reducing the chance of failure. The calculation of the critical buckling load is essential in all structural analysis design because it leads to the design and construction of more durable structures.

Euler’s formula is widely used in structural engineering calculations, but one alternative sometimes used is the Perry-Robertson theory. This is employed in the guidelines set out in Eurocode 3: Design of steel structures. The mathematical instability (i.e. buckling) of a structural member such as a beam or column is calculated for all available steel members and the results are tabulated. Hence, the time taken to design hundreds of structural members is reduced due to the tabulated results readily available for use in everyday structural design.