Aperiodical guest author Andrew Taylor writes about an intriguing piece of number theory which turns out to also be something else.
How many ways are there of writing some natural number $n$ as the sum of two squares?
$$ n = p^2 + q^2 $$
I don’t want an answer for some particular $n$. I don’t even want a general formula. I just want to know… on average.
We’re going to be fairly generous about what we count here, so for $n = 1$ there are four ways: $0^2 + 1^2$, $0^2 + -1^2$, $1^2 + 0^2$ and $-1^2 + 0^2$. There are another four solutions for $n = 2$: $1^2 + 1^2$, $1^2 + -1^2$, $-1^2 + 1^2$ and $-1^2 + -1^2$. But then there are no ways to make $3$. In fact (I claim, with exactly zero formal proof) most numbers can’t be made — but then there are $160$ ways to make $4,005,625$. You’ll find $3,184,193$ unmakable numbers along the way.
So what does that mess of zeroes and hundreds average out at?
Take a guess, there’s no harm in it. Or you can compute it fairly easily — it converges after a few thousand values of $n$. But there’s a much nicer way.
First we need to be a little more formal: we can’t directly take the average over all the natural numbers because there are infinitely many of them — but we can take the average over a finite number $N$ and then find the limit of that average as $N$ tends to infinity.
$$
\text{Average} =
\lim_{N \to \infty}
\frac{ \sum_{n=1}^{N} f(n) }
{ N }
$$
where $f(n)$ is the number of ways to make $n$.
But that’s the same as saying “how many ways can you make $N$ or any number smaller than $N$“.
And that’s the same as saying “out of all possible pairs of numbers, how many of them make a number less than or equal to $N$ if you add their squares”, which I’ll grant is a mouthful — but it’s a mouthful we can work out.
Because we can plot all possible pairs of numbers on a graph

And by Pythagoras, the ones whose squares sum to $N$ or less are the ones enclosed by a circle of radius $\sqrt{N}$ around the origin. Here are the circles up to $N = 9$:
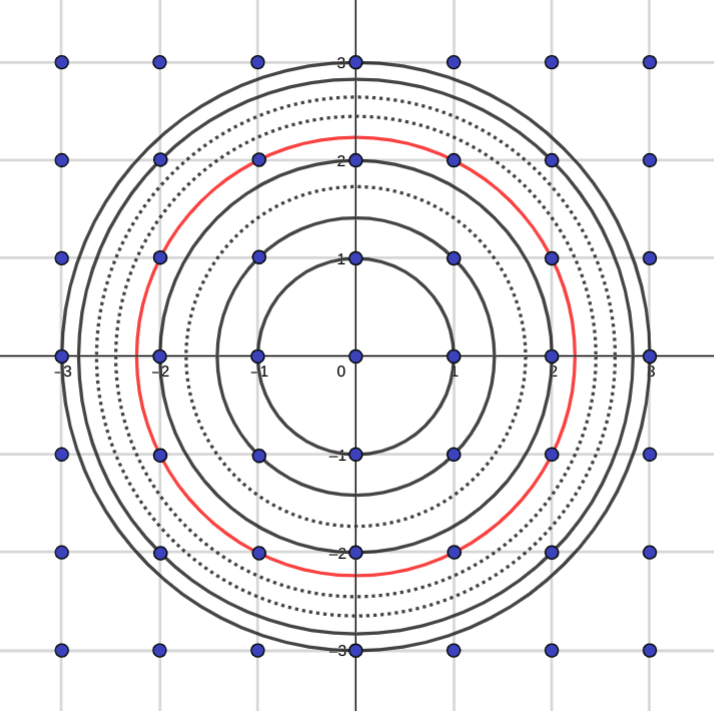
And since the dots are in a square grid with a spacing of exactly $1$, for any reasonably large circle, the number of dots inside it is more-or-less exactly the same as the area of the circle. Just count the squares — this is classic junior school maths lesson area measurement.
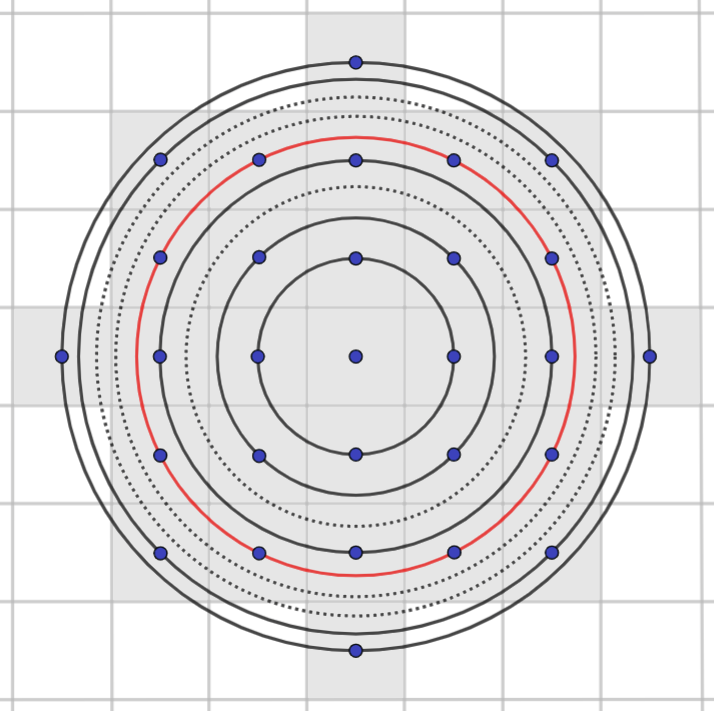
And the area of the circle is obviosuly $\pi r^2$, which is to say $\pi \left ( \sqrt{N} \right )^2$, which is to say $\pi N$.
Which means that for large values of $N$, $\sum_{n=1}^{N} f(n) \approx \pi N$.
So the average number of ways we can make a natural number $n$ as the sum of two squares…
$$
\text{Average} =
\lim_{N \to \infty}
\frac{ \sum_{n=1}^{N} f(n) }
{ N }
= \pi
$$
And that rather blew my mind.
Although in my case, my mind was blown kind of backwards, because my first experience of this cute quirk of mathematics was this post on Mastodon:
“Every now and again one comes across an astounding result that closely relates two foreign objects which seem to have nothing in common. Who would suspect, for example, that on the average, the number of ways of expressing a positive integer $n$ as a sum of two integral squares, $x^2 + y^2 = n$, is $π$?”
— Ross Honsberger, Mathematical Gems III, 1977
This was presented with no context or proof, so I should thank Colin for providing the latter. If you fancy joining in with this frustrating but ultimately rewarding chatter, then Christian runs a maths-focussed server at the nearly unpronouncable mathstodon.xyz.
Very nice! Happy belated pi day…
I should have guessed it was probably pi, given this was posted on 3/14…