This post contains spoilers for the end of Avengers: Infinity War.

Intergalactic population dynamicist Thanos starts 2018 superhero epic Infinity War with a clear goal: he wants to wipe out half of every population in the universe. His planet, Titan, underwent a terrible disaster because of outgrowing limited resources. He sees himself as the saviour of the peoples of the universe because by shrinking all populations by 50%, he can save them from the same fate. Like a good film protagonist, he faces obstacles and people who want to stop him on his quest, in the form of the Avengers and others, but ultimately, with his last ounce of energy, he achieves his goal. Snap.

What effect would that have?

Modelling population growth

A basic model of population growth is simply to consider that the rate of increase of population with respect to time, \(t\), is proportional to the current number in the population, \(N\). The more members of a population, the more babies. Simple. That is,

\[ \frac{\mathrm{d}N}{\mathrm{d}t} ~~\propto~~ N \text{.} \]

This is a very simple model because it just allows growth to continue unchecked without any restrictions caused by lack of resources or other limits. Adaptions can be made to the model to account for limited resources. Thanos, though, seems to think population growth will continue regardless of resources until terrible disaster strikes, so let’s make the same assumption.

The above proportional relationship can be expressed as an Ordinary Differential Equation (ODE):

\[ \frac{\mathrm{d}N}{\mathrm{d}t} = rN \text{,} \]

where \(r\) is the growth rate. If we let the population at time \(t=0\) be \(N_0\), then we can solve this equation to give

\[ N = N_0 e^{rt} \text{.} \]

Given a particular population’s \(N_0\) and \(r\), we can make predictions about population growth. Let’s try an example.

Say a population contains a million people in year 0. Then if we measure populations in millions we can set \(N_0=1\) so

\[ N = e^{rt} \text{.} \]

Say our unsustainable and unrestrained population has grown to 1.5 million in year \(t=5\). Then we can say

\[
\begin{align*}
1.5 &= e^{5r}\\
\ln(1.5) &= 5r\\
r &= \frac{\ln(1.5)}{5} \approx 0.081\text{.}
\end{align*}
\]

Now we have values for \(N_0\) and \(r\), we can make predictions about the growth of our population.

Let’s see what happens to the population after 100 years.

\[ N = e^{100 \ln(1.5) / 5} \approx 3325 \text{,}\]

that is, about 3.3 billion.

Instead, let’s say Thanos’s snap came in year 50. At this point, the population was

\[ N = e^{50 \ln(1.5) / 5} \approx 58 \text{,}\]

and so the snap would set up a new equation from that point with a new \(N_0=29\) (now considering year 50 to be \(t=0\)):

\[ N = 29 e^{t \ln(1.5) / 5} \text{.}\]

Now, thanks to Thanos’s saving grace, the population wouldn’t reach the horribly unsustainable level of 3.3 billion until:

\[ \begin{align*} 3325 &= 29 e^{t\ln(1.5) / 5}\\ \frac{3325}{29} &= e^{t\ln(1.5) / 5}\\ \frac{5}{\ln{1.5}} \ln\left(\frac{3325}{29}\right) &= t \approx 58.475 \text{,} \end{align*} \]

that is, sometime in the 108th year. If 3.3 billion was an unsustainable level, Thanos can sit down to rest at the end of Infinity War safe in the knowledge he has given our population a little over eight years respite.

Populations interacting

Populations are not always as simple as all that, even if we don’t consider most of the necessary resources. Some populations interact with each other as predator and prey. If the prey population falls, there is less food for the predators and the predator population falls. With fewer predators around, the prey population has the opportunity to recover. As the prey population grows, so too does the food supply for the predators. And the cycle continues.

A simple model that exposes this dynamic is the Lotka-Volterra system of equations:

\[ \begin{align*} \frac{\mathrm{d}x}{\mathrm{d}t} &= \alpha x – \beta xy \text{;}\\ \frac{\mathrm{d}y}{\mathrm{d}t} &= \delta\beta xy – \gamma y \text{,} \end{align*} \]

where \(x\) is the prey population, \(y\) is the predator population, \(t\) is time and \(\alpha\), \(\beta\), \(\gamma\) and \(\delta\) are parameters encoding interactions between the populations.

Following a tutorial, it is possible to solve these equations numerically in Python. Say \(\alpha=1\), \(\beta=0.1\), \(\gamma=1.5\) and \(\delta=0.75\). Set the initial prey population to 20 and the initial predators to 6. Then the population levels grow and decline in a regular cycle.

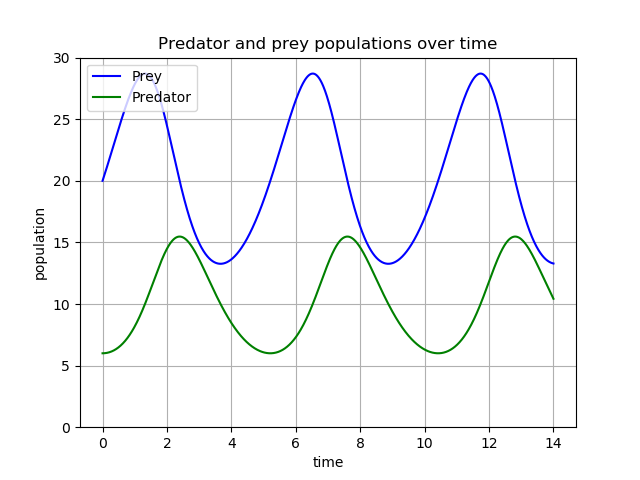
The question, then, is what effect Thanos’s snap would have on this dynamic? Say at \(t=14\) the snap occurs. Both populations are halved, so what does the graph look like after this point?

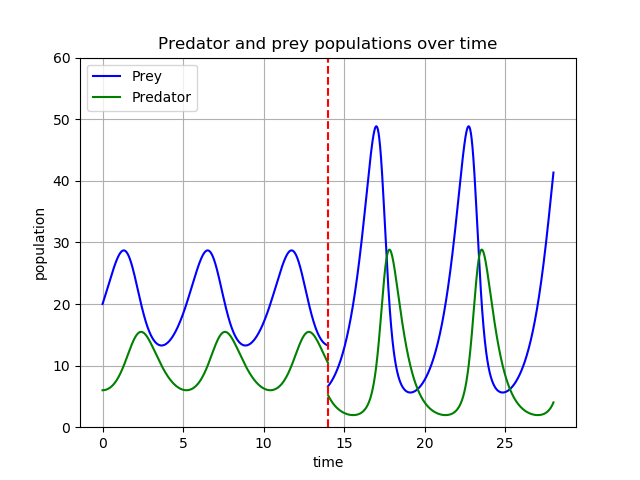
Immediately after the snap, with a sudden decrease in prey as the predator population was already in the decline part of the cycle, the predator population declines quite seriously. With a reduction in predators, the prey population grows to an unprecedented size. With such an abundance of prey, the predator population grows also much bigger than before. This large number of predators causes a severe decline in prey, and a new cycle has been entered.

The new dynamic caused by the snap has both populations growing larger than before and declining lower, meaning this new dynamic is substantially different to what came before. The model doesn’t take external effects into account, but possibly this quite different dynamic might have other consequences in the environment or on other populations. Another factor not taken into account by the model is extinction. It is possible that the new low achieved by the predator population in the time following the snap might cause such a decline that the population can’t recover (the model doesn’t allow for this). Either way, it does not seem likely that this new population dynamic is more sustainable than what came before.

Avengers: Endgame predictions

It’s a few years since the snap. Some populations have already grown back to the levels they were at before, and others have suffered catastrophic collapse. Thanos realises his error and uses the Time Stone to undo the snap, enrolling in a university course on sustainable development instead. Runtime: 5 minutes.