This is the seventeenth match in our group stage: from Group 1, it’s Alex Corner up against Alaric Stephen. The pitches are below, and at the end of this post there’s a poll where you can vote for your favourite bit of maths.
Take a look at both pitches, vote for the bit of maths that made you do the loudest “Aha!”, and if you know any more cool facts about either of the topics presented here, please write a comment below!
Alex Corner – The wobbly table theorem

Alex Corner is a lecturer at Sheffield Hallam University interested in category theory and maths education. You can find him as Fabstract Nonsense on Twitter at @alexcorner.
This is my favourite application of mathematical analysis, using the intermediate value theorem:
If a continuous function, $f$, with an interval, $[a, b]$, as its domain, takes values $f(a)$ and $f(b)$ at each end of the interval, then it also takes any value between $f(a)$ and $f(b)$ at some point within the interval.
If you’ve ever sat down in a pub or café, then you’ll probably have come across a wobbly table, just as I did when I sat down to write this post.
The typical solution is to wedge lots of beer mats under one of the legs. But maths can save the day! Of course, if it involves maths, then we need some assumptions:
- the table has four legs;
- the legs form a square;
- all legs are the same length;
- the floor is not too uneven.
Now the simple fix is as follows. Keep the centre of the table fixed above the same point. Then rotate the table around this point. At some point before you have rotated through 90 degrees, the table will be stable! From experience, this works best with a four-legged, round-top table. Caveats:
- Everybody around the table might swap drinks, a bit like the Hatter’s mad tea-party: all change!
- Upon encountering a wobbly table with your friends, they may exclaim such things as “Do we have to?”, “Don’t get them started”, or “You know what? Let’s just stand”.
There’s an excellent Numberphile video with Matthias Kreck which goes through the ideas behind why this works.
If you’d like to look a little further then there’s also a great video from @Mathologer. The first couple of minutes can certainly help visualise what is going on and the rest goes into a bit more detail as to how the proof works and what we can do to play around with the assumptions.
Alaric Stephen – Alaric’s Sieve

Alaric Stephen is one of the two hosts of the recreational maths podcast Odds and Evenings. He’s currently teaching Maths and Engineering at Hereford Sixth Form College.
Back in 2008, on the train on the way to my university interviews, I was practicing all of the usual proofs in preparation including the proof of √2’s irrationality.
At one point during the proof you need to check the following cases:
- An odd number squared is an odd number.
- An even number squared is an even number.
When reading that you should see that it is at least likely to be true, even by just doing a few examples in your head. But let us show it.
Let’s take a generic odd number first. Say $(2k+1)$ where $k$ is any positive number. Let’s now square it to see what happens. $(2k+1)^2 = 4k^2 + 4k + 1$ which can be written as $2(2k^2 + 2k) + 1$ which can be seen as $2 \times (\text{any number}) + 1 = \text{even} + 1 = \text{odd}$. So yes, an odd squared is odd.
By doing the same thing for even numbers, take $2k$, square it and see what happens. $(2k)^2 = 2(2k^2) = \text{even}$.
This is all well and good, nice when maths works out. So I had this result out on the train and then I thought, what happens if I extend this to multiples of 3 rather than 2?
So instead of evens and odds, which could be more helpful described as multiples of two and one more than multiples of two, we have multiples of three, one more than multiples of three and two more than multiples of three. As a short hand I will write them as $3k$, $3k+1$ and $3k+2$.
So let’s try squaring them.
- $(3k)^2 = 3(3k^2)$ so multiple of three.
- $(3k+1)^2 = 3(k^2+2k)+1$ so 1 more than a multiple of 3.
- $(3k+2)^2 = 3(k^2+4k+1)+1$ so 1 more than a multiple of 3.
Now we notice something strange: none of those results lead to 2 more than a multiple of 3. If we rearrange our logic slightly we can conclude that no square number is two more than a multiple of 3.
So if we got a number line, we could cross out all the numbers 2 more than a multiple of 3 as none of them have a chance of being square numbers.

The natural extension is to try it with other multiples and to see what happens. Multiples of 2 didn’t cross any out, but 3 did. When you try multiples of 4 you don’t end up crossing anything extra out, but 5 does:
- $(5k)^2 = 5(5k^2)$
- $(5k+1)^2 = 5(5k^2+2k) + 1$
- $(5k+2)^2 = 5(5k^2+4k) + 4$
- $(5k+3)^2 = 5(5k^2+6k+1) + 4$
- $(5k+4)^2 = 5(5k^2 + 8k + 3) + 1$
So two more and three more than multiples of 5s can’t be touched.
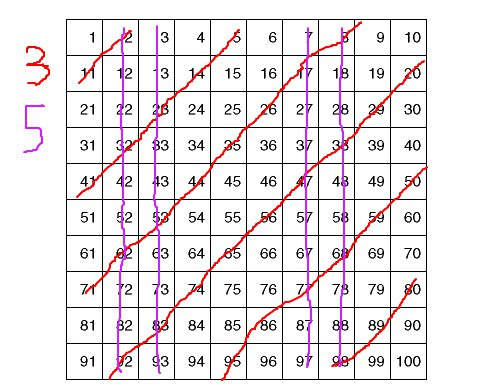
Each time we redo this process we eliminate more and more numbers that can’t be squares.
A note for efficiency of the method, you don’t need to do this method with starting numbers which are non-prime, since they just throw up the same results as their prime factors. So 4 gives the same as 2, 6 gives the same as 2 and 3.
So after the fourth iteration we have:
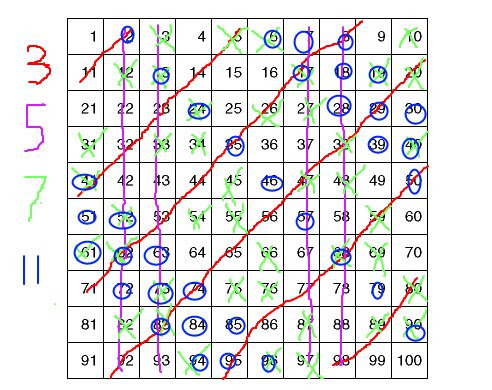
As you can see, the squares are untouched by the colourful destruction around them. I won’t go any further with this colouring, but if you try it yourself you will slowly see more and more of the non squares get crossed out.
However, here’s the problem. How do I know that there isn’t some non-square which isn’t sieved out anywhere along the line?
So at the moment Alaric’s Sieve is still a conjecture. A (bizarrely inefficient) method of finding square numbers and only square numbers. Anybody want to prove it?
During one of the interviews, much to my delight I was asked to prove √2’s irrationality. After quickly rattling through it I presented this method to the interviewer and we spent the rest of the interview working through it together. To this day I’m convinced that this little piece of off-piste mathematics is what got me in and it would be very satisfying to me to finally lay it to rest with a complete proof.
So, which bit of maths do you want to win? Vote now!
Match 17: Group 1 - Alex Corner vs Alaric Stephen
- Alaric with an eponymous sieve (76%, 106 Votes)
- Alex with wobbly tables (24%, 34 Votes)
Total Voters: 140
This poll is closed.
The poll closes at 9am BST on the 18th. Whoever wins the most votes will win the match, and once the group stages are over, the number of wins will determine who goes through to the semi-final.
Come back tomorrow for our eighteenth match of the group stages, featuring Marianne Freiberger and Rachel Thomas against Sameer Shah. Or check out the announcement post for your follow-along wall chart!
I remember having to prove Alaric’s Sieve in a number theory class a long time ago! It follows from an application of Jacobi reciprocity, a wonderful topic. But yes, Alaric, your conjecture is true. :-)
I think Alaric’s conjecture can be proved by hitting it with a big hammer called the local-to-global principle for quadratic forms. But I may be confused. Alaric says that you don’t get to cross out anything new when you look at the modulus 4, but don’t you get to cross out the numbers that are 2 or 3 more than a multiple of 4? Likewise, when you look at the modulus 8, don’t you get to cross out the numbers that are 5 more than a multiple of 8?
Jeff Shallit points out that
https://math.stackexchange.com/questions/1009090/if-a-is-a-quadratic-residue-modulo-every-prime-p-it-is-a-square-without-u
provides an affirmative (but not easy!) answer to the version of Alaric’s question that limits itself to prime moduli.
Thank you for this! I don’t understand it yet, because I’m having to go down the rabbit hole of reading further about almost every theorem it mentions, but I’ll get there.
[ In continuation of my previous comment, here’s a stack exchange post with the proof: https://math.stackexchange.com/questions/646094/is-every-non-square-integer-a-primitive-root-modulo-some-odd-prime/646135#646135 ]
I love that maths is so interconnected, and I love that both of these really interesting pitches have connections with previous pitches. Maybe we need to have a Big Math Off graph, showing connections between pitches?
Here’s a sketch of how I thought about Alaric’s question, of course the link that Jim gave has other ideas too. Maybe other people have more suggestions?
Alaric’s question (if I’ve understood correctly): if we sieve out following Alaric’s procedure, for every prime, is every number left at the end a square?
A rephrasing of Alaric’s question: if a number is not a square, is there a prime for which that number is not a square (so that we cross out the number when we sieve for that prime)? If $a$ is not a square, is there a prime $p$ so that $a$ is not a square modulo $p$?
A slightly different rephrasing of Alaric’s question: if $a$ is not a square, is it the case that there is a prime $p$ so that $a$ is not a square modulo $p$, or $a$ is 2 modulo 4?
I think the answer to the slightly different rephrased question is yes, so that a slight tweak of Alaric’s sieve must give precisely the squares. My slight tweak is that I’m going to cross out all the numbers that are 2 modulo 4 (which we know are not squares). I think this is a reasonable tweak, because we haven’t done anything for the prime 2 but we do learn more from higher powers of 2 (as Jim pointed out). I haven’t thought hard enough about whether the tweak is necessary, maybe others have comments on that.
Here’s an outline of my strategy:
(i) assume $a$ is odd
(ii) show that there is a number $n$ so that the Jacobi symbol $\genfrac{(}{)}{}{0}{n}{a} = -1$ and $n$ is 1 more than a multiple of 4
(iii) use the Law of Quadratic Reciprocity for the Jacobi symbol to deduce that $\genfrac{(}{)}{}{0}{a}{n} = -1$ (this is where it’s useful that $n$ is 1 more than a multiple of 4)
(iv) argue that this means that there is a prime $p$ dividing $n$ such that $\genfrac{(}{)}{}{0}{a}{p} = -1$ (from the definition of the Jacobi symbol)
(v) note that $\genfrac{(}{)}{}{0}{a}{p}$ is actually a Legendre symbol, and so $a$ is not a square modulo $p$.
Note on (i): we can do this because if $a$ is not odd then it is even. If it’s a multiple of 4, then $a = 4b$ where $b$ is also not a square, and we can run the argument for $b$. The prime we find for $b$ will also work for $a$ (if $b$ is not a square modulo $p$, then neither is $4b$). If it’s not a multiple of 4, then $a$ is 2 more than a multiple of 4 and so we have crossed it out in the tweaked version of Alaric’s sieve.
Note on (ii): we can for example do this using the Chinese remainder theorem. Since $a$ is not a square, it has a prime factor $q$ that doesn’t appear to an even power in its prime factorisation. Then there is some $r$ that is not a square modulo $q$. We can use the Chinese remainder theorem to find an $n$ that is 1 modulo 4, that is $r$ modulo $q$, and that is $1$ modulo all other prime factors of $a$. This $n$ will do.
____
Alaric asked whether it’s possible to generalise to higher powers. I don’t know! The argument above is really specifically for squares, because I used quadratic reciprocity. As Jim noted, it’s related to the Hasse principle, or local-to-global principle, and this can go wrong for cubics (as described on that Wikipedia page). I’d need to think much harder about Alaric’s question for cubes and higher powers. Does anyone else have any ideas?