This is the twenty-first match in our group stage: from Group 1, it’s Alex Corner up against Grant Sanderson. The pitches are below, and at the end of this post there’s a poll where you can vote for your favourite bit of maths.

Take a look at both pitches, vote for the bit of maths that made you do the loudest “Aha!”, and if you know any more cool facts about either of the topics presented here, please write a comment below!

Alex Corner – Tantrix

Alex Corner is a lecturer at Sheffield Hallam University interested in category theory and maths education. You can find him as Fabstract Nonsense on Twitter at @alexcorner.

The easiest thing I could do here is link you to a recent podcast hosted by Peter Rowlett and Katie Steckles where I talk to them about the topic at hand. So I will do that but I’ll also say a couple of things and add a few extra visual aids. I’ve tried to provide a number of ways of engaging with this: you can skip this post and watch the numberphile video if you want to just see the mathematics of juggling, you can listen to the podcast, or you can follow the links as you read through this post.

This is a tile from the abstract game Tantrix.

There are fourteen basic tile types in the game when restricting to just three colours which can be seen on the Wikipedia page. Two possibilities, where each edge is connected to its opposing edge, are ruled out.

To make this a bit more mathematical we can redraw each of these as a graph where each edge becomes a vertex and vice-versa.

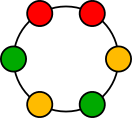
This looks a little bit liked a beaded necklace, so obviously that’s what mathematicians called them.

If we take the necklace and lay it out in a line, and then keep repeating that pattern, we can draw this profile braid. (Imagine that it keeps repeating like this forever.)

Each of the arcs then represents a throw in a juggling pattern. Essentially, a throw which takes an odd number of steps corresponds to a ball swapping hands, whereas a throw which takes an even number of steps will return to the same hand that threw it. The profile braid above can then be thought of as some repeating sequence of numbers:

$$(1,5,2,2,4,4,1,5,2,2,4,4,1,5,2,2,4,4,\dots )$$

Given that it repeats we can just specify it by its repeating elements: $(1,5,2,2,4,4)$. Note that a $2$ is generally considered to mean holding the ball in the same hand without throwing it.

This is essentially the siteswap notation invented by Paul Klimek and further developed by a number of people, including Colin Wright who features in the video below. It can be easier to see where the balls go if we split the profile braid up into a ladder diagram (though I’ve not drawn the rungs), where the top row is the left hand and the bottom is the right.

It’s usually quite easy to find a video of somebody juggling any given siteswap on the internet but this seemed trickier to find. I would have filmed myself but I can barely juggle a normal $3$-ball cascade: $(3)$ in siteswap notation (oddly enough this most standard juggling pattern corresponds to the disallowed tile-types in Tantrix). However there are many great juggling apps, including Gunswap, which I used to generate the following animation.

For an extended introduction to siteswap and the mathematics of juggling, take a look at this Numberphile video featuring Colin Wright. Happy juggling!

Grant Sanderson – Primes and $e$

Grant Sanderson makes videos on the YouTube channel 3blue1brown centered on visualizing math. Once upon a time, he also used to make content for Khan Academy. He’s @3blue1brown on Twitter.

Here’s a question: What does Euler’s number $e$, that famous irrational around 2.71828…, have to do with prime numbers?

To review, primes, like 2, 3, 5, 7, etc. are those whole numbers which have no divisors other than 1 and themselves.  We care about them because all whole numbers can be broken down as a product of primes in a unique way, for example, $\mathrm{2,431}=11\times 13\times 17$, and quite often knowing the prime decomposition of a number is a good first step to understanding other properties it has.  In this way, primes are to number theory what atoms are to chemistry.  But the pattern of primes itself is frustratingly chaotic and difficult to get a handle on, resulting in many famous unsolved questions about this pattern.  Perhaps the most famous example is the 2,300-year-old twin prime conjecture, asking whether or not there are infinitely many pairs of primes just two apart, like (3, 5), (11, 13), (101, 103), etc.

C’mon math!  How do we not have an answer to that?!  We can handle so many problems that seem way more complicated than this.

One thing we know rather well, though, is the approximate density of primes around a given point on the number line.  Among smaller numbers, primes are quite common.  For example, of the numbers from 1 to 20, 8 of them, or 40%, are prime.  As you go higher, they thin out.  Between 100 and 120, only 5 of them, or 25% are prime.  Between 1,000,000 and 1,001,000, 75 of them, or 7.5%, are prime.  And it should make sense that larger numbers are less “likely” to be prime; there are more divisors you have to consider.  But how exactly does this density decrease as you get larger and larger?

For example, I want you to make a guess right now about how long it takes until the density of primes is about 1 in 100.  Really, make an actual guess, and write it down.  Then make a guess for how long until the density is 1 in 1,000.

Enter $e$.

Near the number $e^{10}$, which is about 22,026 the density of primes is about 1 in 10.  If you check this, for example looking for primes in a range of 1,000 numbers centered at this value, you’d find the 101 of them are prime, so the estimate is quite good! Near the number $e^{20}$, which is about 485,165,195, the density of primes will be about 1 in every 20 numbers.  In general, around the number $e^x$, the density of primes is approximately $1/x$.

So back to our guesses: How far do you think you have to go until the density of primes is about 1 in 100?  A trillion?  A quintillion?  Is it bigger or smaller than the number of atoms in the earth?  Well, just plug in $e^{100}$, which is about

$$\mathrm{26,881,171,418,161,354,484,126,255,515,800,135,873,611,118.773}\dots$$

or $2.68\times {10}^{43}$.  It’s not quite up to the number of atoms in the earth, which is closer to ${10}^{49}$, but I bet that’s much higher than you’d have expected!  What about how long until the density is around 1 in 1,000?  Well, you have to get all the way up to $e^{\mathrm{1,000}}\approx 1.97\times {10}^{434}$.  It’s hard to overstate just how huge that number is.  By comparison, the estimated number of atoms in the universe is about ${10}^{80}$.  So even if each atom of the universe had enclosed within it its own copy of the universe, and each of those tiny universe atoms had their own copy of the universe, and so on for two more iterations, the total number of tiny-tiny-tiny-tiny atoms would still only be up to ${10}^{400}$.  The primes do thin out, true, but they do so very slowly.

Going the other direction, if you want to know the approximate density of primes near any number, say near $\mathrm{1,000,000}$, you ask the reverse question: $e$ to what power equals $\mathrm{1,000,000}$?  That is, you take the natural log: $\ln (\mathrm{1,000,000})\approx 13.81$.  The reciprocal of this number gives you the density of primes, in this case, $1/\ln (\mathrm{1,000,000})\approx 0.072$.

How is this used?

This actually offers a nice heuristic for making quantitative predictions about prime numbers, known as the “Cramér random model”, named for 20th-century Swedish mathematician Harald Cramér.  In this model, you treat the prime numbers as if they came from a random distribution where each number $n$ has a probability of $1/\ln (n)$ of being included.  One must obviously take this with a heavy grain of salt since the primes are not random, but the idea is that many they exhibit many of the statistical patterns you might expect from such a distribution.

For example, how would you guess how many primes there are between 1 and $\mathrm{1,000,000}$?  Using the Cramér model, you could count through every whole number and add a weight for each one according to the “probability” that it’s prime.  That is, you take the sum $\sum _{n=1}^{\mathrm{1,000,000}}\frac{1}{\ln (n)}$.  More often, instead of this sum, you might come across the integral ${\int }_0^x\frac{dt}{\ln (t)}$, which is a continuous analog approximating this sum, and easier to compute for those savvy with calculus.  This integral does indeed offer a really good estimate on the count of primes below a given value $x$.  In fact, for those of you familiar with the Riemann hypothesis, one of the big implications it would have if it turns out to be true is that this “logarithmic integral”, as it’s called, is really close to the actual count of primes.

Of course, there are some ways that the Cramér model is obviously terrible.  For example, it would suggest that “probability” that two adjacent numbers $n$ and $n+1$ are both prime is about $\frac{1}{\ln (n)}\frac{1}{\ln (n+1}$.  But of course, once you get bigger than 2, two adjacent numbers can never be prime!  One of them will always be even.  Massaging the model slightly, you can account for certain obvious correlations like this, e.g. that number right next to each other can’t both be prime, and produce certain statistical estimates on groups of primes, like twin primes, which line up quite closely with numerical evidence.

The specifics of this are spelled out in something known as the “prime $k$-tuples conjecture”, which is like the twin prime conjecture on steroids, originally proposed by Hardy and Littlewood.  It doesn’t just ask whether twin primes are infinite, it offers a specific quantitative statement about their approximate density.  As number theorist James Maynard put it in a Quanta article from a few years ago, “Most mathematicians believe the twin primes conjecture not so much because they keep finding more twin primes, but because the number of twin primes they’ve found fits so neatly with what the prime $k$-tuples conjecture predicts.”  Moreover, it does this not just for twin primes, pairs that look like $(n,n+2)$, but for every conceivable pattern of primes, for example, tuples that look like $(n,n+2,n+6,n+12)$, or whatever other constellation you might dream up.

And it all begins with the model that a randomly chosen number near $e^x$ has about a 1-in-$x$ chance of being prime.

So, which bit of maths do you want to win? Vote now!

 Loading ...

The poll closes at 9am BST on the 22nd. Whoever wins the most votes will win the match, and once the group stages are over, the number of wins will determine who goes through to the semi-final.

Come back tomorrow for our twenty-second match of the group stages, featuring Marianne Freiberger and Rachel Thomas against Jorge Nuno Silva. Or check out the announcement post for your follow-along wall chart!