Our mathematical face-off continues with our second match: from Group 2, it’s Marianne Freiberger and Rachel Thomas competing as a single mathematical unit vs Vincent Pantaloni. Their pitches are below, and at the end of this post there’s a poll where you can vote for your favourite bit of maths.

Take a look at both pitches, vote for the bit of maths that made you do the loudest “Aha!”, and if you know any more cool facts about either of the topics presented here, please write a comment below!

Marianne and Rachel – The Sydney Opera House

Marianne and Rachel are co-editors of Plus magazine, a free online magazine about maths aimed at a general audience. They have also written three popular maths books and edited one.

Architecture has provided some of our favourite mathematical stories over the years: the way maths can create brilliant experiences inside a building (such as that for cyclists and spectators inside London’s Olympic Velodrome); and how it makes much of modern architecture possible. We came across this story when we were writing our book, Understanding numbers. We think it is particularly lovely as it captures both the creativity, problem solving and power of thinking mathematicially.

On 29 January 1957, when Jørn Utzon’s sail-like sketches were announced as the winning design for the Sydney Opera House, Utzon had a problem — he didn’t know exactly how he would build them. The problem still wasn’t solved two years later when construction began on 2 March 1959.

Inspired by the harbour location, the young Danish architect had envisioned a series of sweeping curved shells. But in order to build these shells the shapes had to be described mathematically to accurately calculate all the loads and stresses on the building. When asked by the engineers to specify the curves Utzon bent a ruler to trace the curves he wanted. Over the next four years they tried various mathematical forms — ellipses, parabolas — to try to capture Utzon’s design.

Finally, in October 1961, Utzon found the “key to the shells”: every sail was formed from a wedge cut from a single sphere (and its mirror image). This ingenious solution not only provided a mathematical description of the roof of his design, it also solved all the problems of constructing such a complex structure. Previously each shell appeared to be different, and it would have been almost impossible, both in terms of engineering and finance, to construct these huge bespoke parts. Instead, with shells having a common spherical geometry (based on a sphere with radius of 246 feet), they could instead be constructed by standard parts that could be mass produced and then assembled.

Describing the design mathematically made it possible to create one of the most iconic buildings in the world. The mathematics of the design also exemplified Utzon’s artistic vision, providing “full harmony between all the shapes in this fantastic complex”.

Vincent Pantaloni – Lines on a torus

Vincent Pantaloni is a French maths inspector who co-authored with Ed Southall the books Geometry Snacks and More Geometry Snacks. He shares some mathsy GIF animations made with GeoGebra on Twitter as @panlepan.

Pac-Man lives on a torus

A simple way to create a 2D game such as Pac-Man where you stay on a rectangular (eg square) board without being blocked by the edges is to connect the opposite edges together. When doing so, it’s as if Pac-Man was evolving on the surface of a torus. We’ll see what happens on the torus when you follow straight lines on this square.

When you just connect the blue lines together you get a cylinder, and then, connecting the red lines forms a torus.

Straight lines on a torus

Here’s what happens if Pac-Man follows a straight line of slope 1/2. A way to plot this is to have a point $M(x,y)$ moving on the straight line in the plane and then create the yellow point with coordinates $(x \mod 1, y \mod 1)$ or in other words the fractional parts of $x$ and $y$ : $x-\lfloor x \rfloor$ and $y – \lfloor y \rfloor$ where $\lfloor x \rfloor$ is the integer part of $x$.

In both figures, following the yellow line means that if you run by 1 blue step, you rise by 2 red steps.

Have fun playing tic-tac-toe (3 in a row) on a torus.

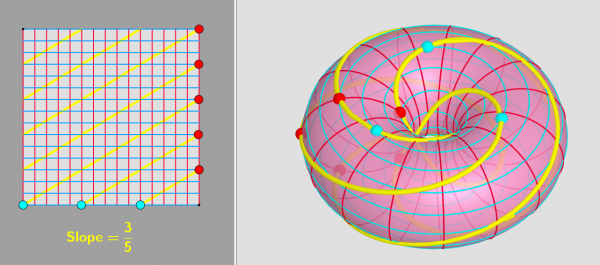
To read the slope of a line on a torus you can proceed as you would in the plane (rise/run) if you have a grid and spot two points on the nodes:

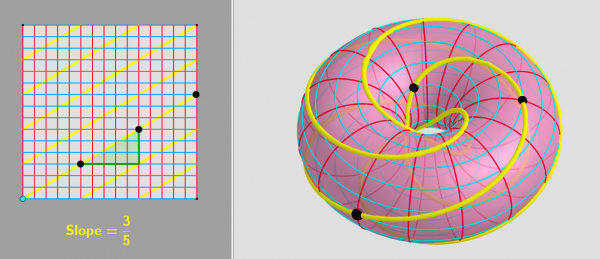
Another method is illustrated here, you just have to count how many times the spirally line cuts any red circle and divide it by the number of times it cuts any blue circle. You can see that the line goes 3 times into the hole while it is wound 5 times around the doughnut.

What if…

OK, so if the slope is a rational number we get it, we have a knot where we just have to count the number of turns in one direction and in the other, to find out what it looks like. What if the slope is an irrational number ? Of course you can’t draw what the knot looks like for an irrational slope but you can choose rational slopes closer and closer to the irrational number. (eg for $\sqrt2$ you could choose 1.4, then 1.41, 1.414, etc.)

You can interact with a Geogebra applet here to move the torus around and change the slope. Clicking on the buttons gives specific values to the slope, clicking “slider” allows you to change the slope with a step of 0.1.

For 1.41 the knot seems to almost cover the torus, but it’s still a loop.

How many times does it wind around the torus?

When you draw a straight line say $y=ax$ in the plane, either $a \in \mathbb{Q}$ so there exists $p$, $q$ in $\mathbb{Z}$ coprime such that $a=p/q$ and in that case the line hits nodes of the $\mathbb{Z}^2$ lattice infinitely many times, at every $(k \cdot q, k \cdot p)$ for $k \in \mathbb{Z}$ or $a$ is an irrational number and the line never hits any node of the $\mathbb{Z}^2$ lattice except $(0,0)$ but gets arbitrarily close to them. For the torus, this dichotomy gives either a good looking knot or a line dense in the torus.

Circles on a torus.

Now why stop with straight lines on a torus? I had some fun drawing circles on the planar representation of the torus. Below is a circle with an increasing radius.

Let’s see what this produces on the torus. If the radius $r$ is such that $r<0.5$ you have a simple loop, and when $r>0.5$ the curve crosses itself.

You can interact here with a geogebra applet to see more of these circles.

Just to make you dizzy I’ll leave you with some of these circles rotating on the torus and a question: are these really circles on the torus? I mean, do they represent the set of points on the torus that are at a fixed distance (to be defined) from a given point?

If you wonder why I chose to colour the torus in pink, it’s because of the Geometry Snacks cover. No torus inside, just on the cover. :-)

So, which bit of maths has tickled your fancy the most? Vote now!

 Loading ...

The poll closes at 9am BST on the 3rd. Whoever wins the most votes will win the match, and once the group matches are all done, the number of wins will determine who goes through to the semi-final.

Come back tomorrow for our third match of the group stages, pitting Vicky Neale against Jim Propp. Or check out the announcement post for your follow-along wall chart!