This is the tenth match in our group stage: from Group 2, it’s Vincent Pantaloni up against Jorge Nuno Silva. The pitches are below, and at the end of this post there’s a poll where you can vote for your favourite bit of maths.

Take a look at both pitches, vote for the bit of maths that made you do the loudest “Aha!”, and if you know any more cool facts about either of the topics presented here, please write a comment below!

Vincent Pantaloni – A cone, a sphere and a cylinder

Vincent Pantaloni is a French maths inspector who co-authored with Ed Southall the books Geometry Snacks and More Geometry Snacks. He shares some mathsy GIF animations made with GeoGebra on Twitter as @panlepan.

One of the greatest geniuses, Archimedes, managed to prove that a sphere, its circumscribed cylinder and a cone (same diameter and same height as the cylinder) had volumes that were in a simple ratio without knowing the formula for these volumes!

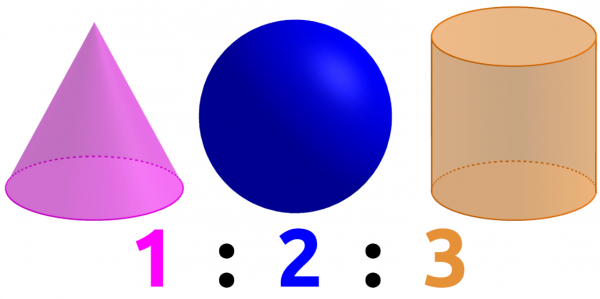
He actually already knew the ratio 1:3 for the cone to the cylinder, the sphere is much more tricky to squeeze in here. His proof is a true beauty of maths for several reasons. Archimedes used what he called the Mechanical Method, also referred to as The Method and which takes the form of a letter from Archimedes to Eratosthenes, the chief librarian at the Library of Alexandria, and contains the first attested explicit use of indivisibles (sometimes referred to as infinitesimals). The work was originally thought to be lost, but in 1906 it was rediscovered in the Archimedes Palimpsest.

It is called the “mechanical method” because it relies on the law of the lever, which was first demonstrated by Archimedes.

I’ll sketch the proof below with some animations. More details are given in the slideshow below that I used for a talk I gave at #latemaths in London last fall. 

Archimedes first considered this lovely simple 2D figure with a square, a diagonal and a semicircle:

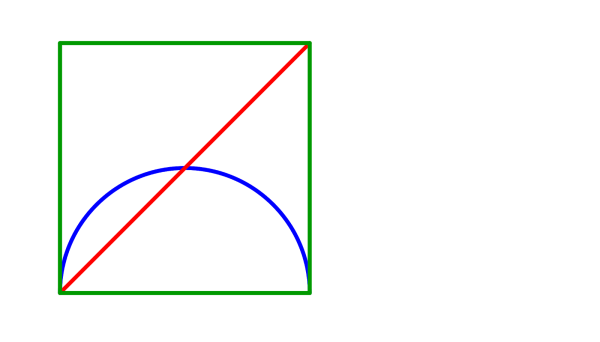
Then, considering this vertical line he established this identity with ratios using the different lengths.

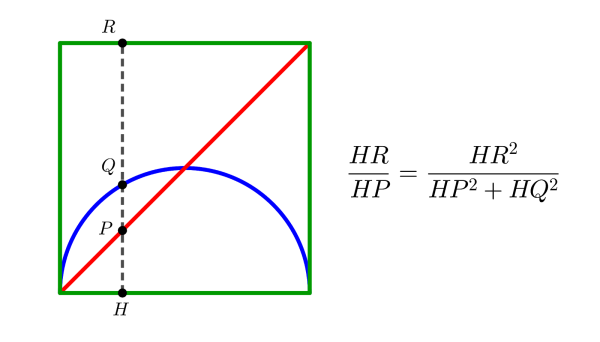
Which is true no matter where the vertical line is. You’ll find a proof of this in the slideshow below, but it’s a nice puzzle with several possible methods.

His first great idea is to link this with what he discovered about levers illustrated below with an example. The lengths of the arms are inversely proportional to the weights on each arm.

Today we’d say that the momentum (weight × distance to the axis) is the same on both sides.

So you can balance some squares as shown on the animation below:

You can do it for squares but also for discs because their area is proportional to the square of their radius:

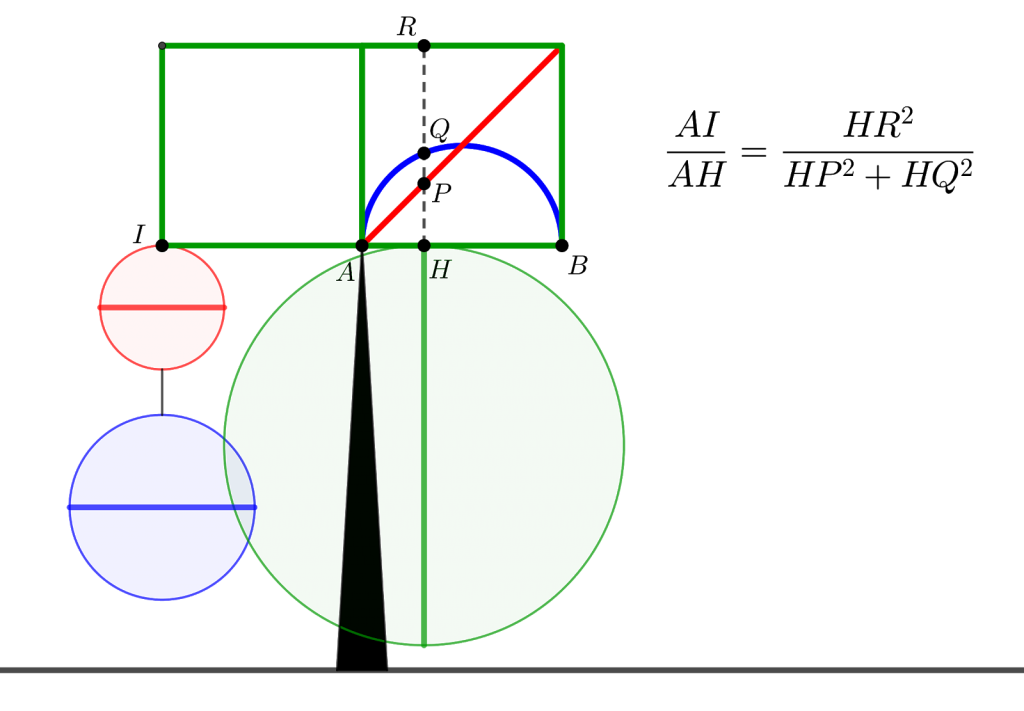
Now, another genius idea that Archimedes had was to sum all of these. We call this integration nowadays, it’s an infinite sum.

For each position, there’s an equilibrium so it’s also true for the sum!

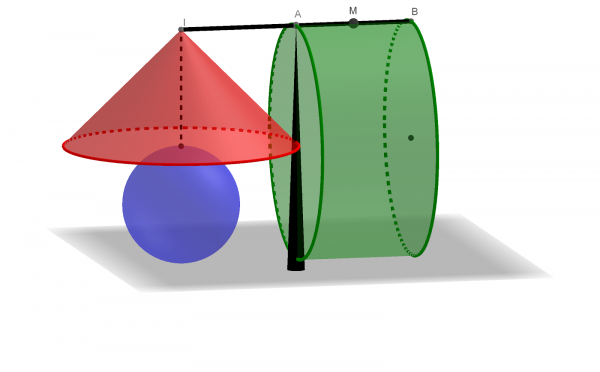
The cone and sphere formed are hanging from point I, but the cylinder needs to be considered as hanging from the midpoint M of [AB]. That means that the volume of the green cylinder is equal to two times the volume of a blue sphere and a red cone:

Scaling the green cylinder’s base and the cone’s base by ½ (so their volumes by ¼) and knowing that the volume of the cone is one third of the volume of the cylinder, Archimedes finally managed to prove this beautiful ratio of volumes. Today we’d write:

4 Cylinders = 2 Spheres + 8 Cones and 1 Cylinder = 3 Cones so: 1 Sphere = 2 cones.

Details are given in the slideshow, without using algebra.

Since 1+2=3 (duh!) and the volume of the cone is the same as that of two cones with half this height, you get a lovely figure where the missing volume between that of the cylinder and that of the sphere is filled by the (double) cone.

Jorge Nuno Silva – Latin Erdős

Jorge Nuno Silva is a Portuguese mathematician (PhD UCBerkeley 1994), President of Ludus and Professor at the University of Lisbon (Department of History and Philosophy of Science). He is an editor of Recreational Mathematics Magazine and Board Game Studies Journal.

So, which bit of maths do you want to win? Vote now!

 Loading ...

The poll closes at 9am BST on the 11th. Whoever wins the most votes will win the match, and once the group stages are over, the number of wins will determine who goes through to the semi-final.

Come back tomorrow for our eleventh match of the group stages, featuring Jim Propp and Sophie Carr. Or check out the announcement post for your follow-along wall chart!