This is the fourteenth match in our group stage: from Group 2, it’s Vincent Pantaloni up against Sameer Shah. The pitches are below, and at the end of this post there’s a poll where you can vote for your favourite bit of maths.
Take a look at both pitches, vote for the bit of maths that made you do the loudest “Aha!”, and if you know any more cool facts about either of the topics presented here, please write a comment below!
Vincent Pantaloni – The Cantor Tartan

Vincent Pantaloni is a French maths inspector who co-authored with Ed Southall the books Geometry Snacks and More Geometry Snacks. He shares some mathsy GIF animations made with GeoGebra on Twitter as @panlepan.
The Cantor set is one of the things that math nerds like because it has many cool properties. My friend and co-author Ed Southall even has a Cantor set tattoo ! In the Cantor family of weird sets, I give you the Cantor Tartan which has this awesome and surprising property :
Any rectangle with dimensions smaller than one can be covered by the Cantor Tartan.
Hands on! Print a picture of the Cantor Tartan, cut a rectangle out of a piece of paper and try to make its sides correspond to some lines on the Cantor Tartan. Here is a pdf to print with the Cantor Tartan and some rectangles. You’ll see it’s not very easy to find a position on the tartan, but I’ll give you a geometrical method that also proves that it is always possible.
What is this Cantor Tartan?
If $C$ denotes the Cantor set, the Cantor Tartan is $(C \times [0,1]) \cup ([0,1] \times C)$. In case you’re not familiar with the Cantor set, the following animation suggests a recursive construction of $C \times [0,1]$ starting from a unit square and by erasing the central third strip from rectangles.
These are just the 5 first steps, imagine you continue the process indefinitely, and then you rotate a copy of that 90° to get the Cantor Tartan $(C \times [0,1]) \cup ([0,1] \times C)$:
With the GeoGebra applet below, you can drag the blue point around to change the dimensions of the rectangle and see a possible position of a congruent rectangle on the Cantor Tartan.
OK, but why does it work?
The property with the rectangle is a consequence of the following:
For any number $a$ in $[0,1]$, there exists two numbers $x$ and $y$ in the Cantor set such that $a=y-x$.
In other words, for any $a$ in $[0,1]$ the straight line $y=x+a$ intersects $C \times C = C^2$. To see why this is true, look at the animation below.
You can also find an algorithm to determine $x$ and $y$, based on their writing in base 3, knowing that C is the set of numbers in [0,1] which have no 1 when written in base 3. Spoiler and inspiration on Cut The Knot.
$C^2$ can be obtained by repeatedly removing the open cross formed by the five squares from a square split in 9 congruent squares, thus leaving each time the four closed square corners.
Whatever the value of $a$ is ($a \in [0,1]$) the red line intersects one of the 4 big closed squares of side 1/3 in the corners. In such a square it will therefore intersect one of the four squares in its corners, and so on… We have a decreasing (for inclusion) sequence of closed squares, so the limit point exists and is in $C^2$. QED
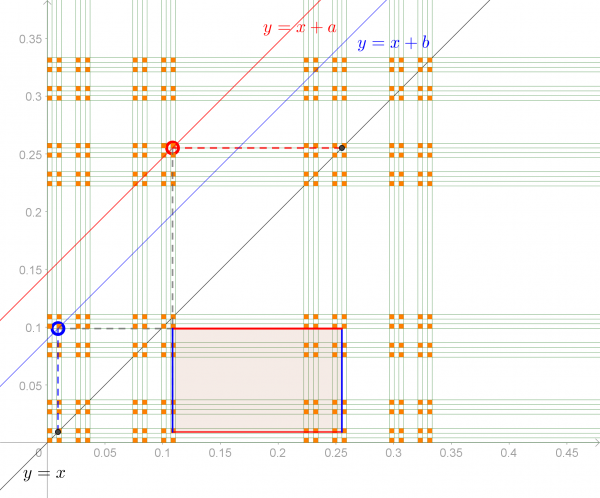
Here’s a method to place any rectangle with dimensions $a \times b$ on the Cantor Tartan:
On the figure below, I drew an approximation of $C^2$ (in orange) and of the Cantor Tartan (in green).
Draw the lines $y=x$ and $y=x+a$ and consider an intersection point $I = (i,j)$ of $y=x+a$ and $C^2$ (in the red circle). You then have $a=j-i$ which gives you the red dashed line of length $a$. Repeat this for the width $b$ of your rectangle (see blue line and circle), and the construction of a rectangle with dimensions $a \times b$ in the Cantor Tartan follows as illustrated below.
Sameer Shah – The Unfolding of a Magic Trick

Sameer Shah has been teaching high school math in Brooklyn for the past twelve years. You can read his musings about his classroom at Continuous Everywhere but Differentiable Nowhere. He’s @samjshah2 on Twitter.
You stand in front of a classroom of students with a standard deck of cards in your hands. You shuffle the cards and hand them to the audience. Any and all of your kids get to shuffle them and organize them however they want. You appoint one leader from the audience to represent the audience. They take the shuffled deck around and have five people select one card each. The deck of 52 cards now has 47 cards in it. The leader puts these 47 cards in the back of the room, far away from you.
The audience leader then takes the five cards and holds them up for the class to see, but not you. You tell the leader to choose one of them, but not reveal to you which one. They hold the five cards up, contemplates, rearranges them, contemplates some more, rearranges them, contemplates. Finally, they choose one special card and announce: “I choose this card to be the secret card.” They show that card to the class but not to you.
The leader hands you the remaining cards. You look at the four cards, tap your head in contemplation, you say some magic words (“By the powers of Ramanujan and Mirzakhani…”), and then with a flourish you tell the audience what the secret card is.
The class has a collective gasp, followed by a moment of stunned silence, followed by whooping and hollering as your students hoist you on their shoulders and parade you around the halls of your school celebrating your mental telepathy abilities.
INCROYABLE! IMPOSSIBLE! But it happened! How did you accomplish this feat? It wasn’t magic. It was mathemagic!
I know you want the reveal… and I’ll give it to you. But I’m going to have the trick unfold in multiple parts. Why? I think it was the winter of 2000 and I was taking a two week math course on random fun math things in college. The professor did this trick, and led the audience through the magical moments one-by-one. (I sadly can’t remember who taught it to me.) It’s in the stunning sequence of logical insight when the impossible becomes possible that my appreciation for the beauty of this trick came through. I want that for you, even if this means the post is going to be a little bit long. (If you just want to skip the beautiful unfolding, ugh, but okay. In the postscript at the end I have a youtube video that shows how this is done.)
Right now, I’m going to give you the first part of the reveal… You and the audience leader are in collusion. The audience leader doesn’t have any control over the five cards the class picked, but the audience leader is on your side.
Before I tell you anything more, take 5 minutes, grab a piece of paper, and see if you can’t figure out the way the audience leader and the teacher colluded! Yes, I’m going to break the code of mathemagicians everywhere and share with you how to do this so you can impress your students! But first, you should try to think this through yourself. (The impossibility of it becomes all the more impressive if you try to figure it out and can’t.
Even when I was told the audience leader and the teacher were in collusion, I still thought the trick was impossible. The audience leader gives the teacher four cards and somehow those four cards should be enough to reveal what the fifth card is. WHAAA?!?
When trying to unpack this trick, I wondered how the audience leader could share information. If you read the setup carefully above, the audience leader arranged the four cards that were given to the teacher. So I realized that somehow the arrangement of the four cards could give the teacher some information about the fifth card. My brain immediately went to brute force. There are $4!=24$ ways to arrange four cards. So for example if the numbers on the cards were 1♥, 5♦, 6♠, J♥, the audience leader and teacher could theoretically do this:
- The smallest card numerically (1) would be A
- The next smallest card numerically (5) would be B
- The next smallest card numerically (6) would be C
- Finally the largest card numerically (J) would be D
(As an important note: You might ask what if you had 2♥, 2♣, 5♦, 5♠? Easy solution. Beforehand, the teacher and audience leader decide an order of suits. So let’s say ♥ > ♠ > ♦ > ♣. So the cards from smallest to largest would be: 2♣, 2♥, 5♦, 5♠.)
I realized if both the teacher and audience leader were good at memorizing, they could spend weeks memorizing some table of values, like:
- The order ABCD=1
- The order ABDC=2
- The order ADBC=3
- …
- The order DCBA=24
And then I thought each ordering of the cards could each represent a card in the deck. (Like 1=1♥, 2=2♥, 3=3♥, …, 11=J♥, 12=Q♥, 13=K♥, 14=1♠, 15=2♠, etc.) But even with all of this memorization, and the audience leader arranging the four cards intentionally, this approach can’t give the teacher enough information to give the missing fifth card. There are 52 cards in a deck, and the audience leader only has a way to “tell” the teacher that the missing card is one of 24 cards.
Even with collusion, this trick still felt impossible!
Okay here’s another hint to think about before the next reveal. Remember that the audience leader gets to pick the secret card which the teacher has to guess. How can the teacher and audience leader use that to their advantage? Take 60 seconds to see if you can figure this out.
Ready for the second reveal? The fact that five audience members each got to choose a card was no accident. Somehow the audience leader needs to tell the teacher the suit of the card they need to guess. Since there are four suits and five cards, at least two of the five cards need to have the same suit. BOOM!
So let’s go back to an example. Let’s say the audience leader has 2♥, 3♠, 3♣, 10♥, and J♦. Since there are two heart cards, the audience leader chooses one of the heart cards to be the card that the teacher has to guess, say the 10♥. So the audience leader put the 2♥ of hearts as the first of the four cards that the teacher gets. The teacher and audience leader make a decision that the first card given tells the teacher the suit of the card the teacher needs to guess. So in this example, putting the 2♥ as the first of the four cards that the teacher gets is a signal that the secret card they’re trying to guess is a heart. And with this one powerful move, the teacher now only has to figure out what the number on this card is.
(Astute readers may ask what should happen if the audience leader has two heart cards and three club cards? No worries… the audience leader can pick the secret card to be a heart or a club. By the end of this trick, you’ll see why!)
But wait… blergity blerg! The audience leader has only three cards left they can use to send information (since the first card was used to send information about the suit and one card is the secret card). But those three cards have to be able to tell the teacher the number of the secret card. How can the audience leader send the teacher the number of the card with those three cards? Okay, take 60 seconds and see if you can figure this out.
Okay, so you can’t. It’s impossible. Let’s look back at our example. The card the teacher is trying to guess is the 10♥. At this point, the teacher has been given the 2♥, which all the teacher knows is that the secret card is a heart.
The audience leader can organize the 3♠, 3♣, and J♦ to somehow reveal the number of the secret card to the teacher. BUT HOW?!?! Like before, let’s think about arranging the cards from low to high: the low card (L) is the 3♣, the medium card (M) is the 3♠, and the high card (H) is the J♦. (Remember we said ♥ > ♠ > ♦ > ♣.)
Like before, the audience leader can arrange these three cards to encode information about the secret card, but now it’s easier since we’re working with 3 cards and not 4, so we can send 3!=6 numbers:
- LMH = 1
- LHM = 2
- MLH = 3
- MHL = 4
- HLM = 5
- HML = 6
Aaaargh! The audience leader is in trouble. There are 12 possible heart cards that the teacher thinks the missing card could be (any of the hearts except the 2♥, which is the first of the four cards they were given). The audience leader can only get across 6 numbers by ordering the three remaining cards.
THIS TRICK IS IMPOSSIBLE!
Or is it? Here’s the last hint. There was a point above when the audience leader got to make a choice. But since they make a random choice, they are losing some information they could be passing along. See if you can figure out when the audience leader made a choice, and if you can use that to your advantage to figure this out. Take 60 seconds to see if you can find the final tweak you can make to make this mathemagic trick work
Time for the last reveal. In our example, we had 2♥, 3♠, 3♣, 10♥, and J♦. The audience leader got to choose whether the secret card was the 2♥ or the 10♥. In this case, the audience leader should have picked the secret card to be the 2♥. This will make sense in a second…
The audience leader gives the teacher the cards in this order: 10♥, J♦, 3♣, 3♠.
The first card tells the teacher the suit (♥), and the next three cards tell the teacher a number (J♦, 3♣, 3♠ which is ordered High-Low-Medium or HLM, which yields 5).
Here’s the crazy cool insight: we take the 10♥ and count up by 5 (cycling back to 1 once we hit the King): J♥, Q♥, K♥, 1♥, and finally 2♥
Done. The card the teacher needs to guess is the 2♥.
Here’s the key insight that allows this to work: any two cards chosen from a suit are 6 “away” from each other.
Let’s make this clearer with two examples:
So if in our five cards, we had a 3♠ and 7♠, the audience leader would choose the 7♠ to be the secret card and give 3♠ as the first card to the teacher. Then they would arrange the remaining three cards to be MHL=4. The teacher then sees the 3♠ and counts up by 4: 4♠, 5♠, 6♠, 7♠. The secret card is the 7♠.
Or if in our five cards, we had a 3♠ and J♠, the audience leader would choose the 3♠ to be the secret card and give the J♠ as the first card to the teacher. Then they would arrange the remaining three cards to be HLM=5. The teacher then sees the J♠ and counts up by 5: Q♠, K♠, 1♠, 2♠, 3♠. The secret card is the 3♠.
In short:
- Of the five cards the audience has chosen, the audience leader looks for two cards of the same suit. They carefully choose one to be the “secret card” and put the other card of the same suit as the first of the four cards to give to the teacher.
- The audience leader quickly arranges the remaining three cards to represent a number from 1 to 6 and puts them in order. This number represents how far “away” the secret card is from the first card.
- The teacher receives the four cards in order. They look at the first card to determine the suit. Then they look at the remaining three cards to determine a number from 1 to 6. The teacher “adds” this number to the first card, and voila! The teacher has just determined the secret card!
Hopefully with the unfolding of the trick with all the reveals, you have seen how the impossible becomes possible. This trick is confounding and stunning. I promise you if your practice this once or twice with a collaborator, you’ll become experts and wow your friends. Ahhh, information theory. MATH, Y’ALL! It’s fantastical!
Check yourself! Here are some quick ways to check if you can do this trick!
If you’re the teacher, and you received these 4 cards in order, determine the secret card:
1) Q♠, 9♥, 4♠, 1♦
2) 3♣, K♣, 4♠, 5♠
3) 7♥, J♥ 6♥, K♠
4) J♠, 4♦, 9♦, 1♥
If you’re the audience leader, and the audience chose these 5 cards, which would you pick to be the secret card, and in what arrangement would you give the remaining four cards to the teacher? (There may be more than one way you can do this.)
5) K♣, J♠, 7♥, 4♦, 6♥
6) 4♥, 7♥, 10♥, 6♥, K♠
7) 3♣, 9♥, 1♥, Q♥, 10♣
8) 8♥, 1♦, 1♣, K♠, 8♦
Solutions:
1) 5♠
2) 8♣
3) 10♥
4) 2♠
5) 6♥, 4♦, J♠, K♣ [secret card: 7♥]
6) 4♥, 7♥, K♠, 10♥ [secret card: 6♥] or
4♥, 10♥, 6♥, K♠ [secret card: 7♥] or
4♥, K♠, 7♥, 6♥ [secret card: 10♥] or
6♥, 4♥, 10♥, K♠ [secret card: 7♥] or
6♥, 7♥, K♠, 4♥ [secret card: 10♥] or
7♥, 6♥, 4♥, K♠ [secret card: 10♥]
7♥, 6♥, 4♥, K♠ [secret card: 10♥]
7) 10♣, Q♥, 9♥, 1♥ [secret card: 3♣] or
9♥ Q♥, 3♣,10♣ [secret card: 1♥] or
9♥, 3♣, 1♥, 10♣ [secret card: Q♥] or
Q♥, 3♣, 10♣, 9♥ [secret card: 1♥]
8) 8♦, K♠, 8♥, 1♣ [secret card: 1♦]
PS. After writing this, I searched online to see if I could find this trick published anywhere. Turns out it has a long history that spans from way before I was shown this in my math class.
- Some history of this trick and variations.
- A great article on the trick by Colm Mulcahy.
- Finally, here’s a youtube video teaching you this trick.
So, which bit of maths do you want to win? Vote now!
Match 14: Group 2 - Vincent Pantaloni vs Sameer Shah
- Sameer with card tricks (67%, 164 Votes)
- Vincent with measureless tartan (33%, 80 Votes)
Total Voters: 237
This poll is closed.
The poll closes at 9am BST on the 15th. Whoever wins the most votes will win the match, and once the group stages are over, the number of wins will determine who goes through to the semi-final.
Come back tomorrow for our fifteenth match of the group stages, featuring Jim Propp and Sunil Singh. Or check out the announcement post for your follow-along wall chart!

You can interact online with this GeoGebra applet of the Cantor Tartan here if you want :
https://ggbm.at/c3npupux
Enjoy !