This is the fifteenth match in our group stage: from Group 3, it’s Jim Propp up against Sunil Singh. The pitches are below, and at the end of this post there’s a poll where you can vote for your favourite bit of maths.

Take a look at both pitches, vote for the bit of maths that made you do the loudest “Aha!”, and if you know any more cool facts about either of the topics presented here, please write a comment below!

Jim Propp – Calculus is Deeply Irrational

Jim Propp is a math researcher/teacher/popularizer on the faculty of the University of Massachusetts Lowell who blogs at Mathematical Enchantments. Jim is active in the Gathering 4 Gardner Foundation, the Global Math Project, and the National Museum of Mathematics. He’s @JimPropp on Twitter.

You’re lying on a beautiful beach when you feel a tap on your shoulder, and suddenly you’re not at the beach at all — you’re in a classroom. The student who woke you looks apologetic, and from the front of the room the teacher is staring at you expectantly. He points at the blackboard on which he has written the function $f(x) = 6x – x^3$ next to its graph. “I said: how can we find the maximum value achieved by this function on the interval from 0 to 2?”

A pleasant dream has been replaced by your worst nightmare. But into your still-sleep-fogged conscious mind rises a catchphrase, your only chance for salvation. “Um… Take the derivative and set it equal to zero?”

The professor beams and tells the class “You see? It’s so easy, you can even do it in your sleep!”

This event took place nearly forty years ago (my friend Dan Ullman was a teaching assistant and saw the whole thing, though the function being maximized and the student’s dream were probably different). The story highlights one feature of doing “cookbook-calculus”: you can survive just following the recipes.

But what I want to talk about is what happens next in that classroom, and its broader significance. Because when you differentiate the function $6x – x^3$ you get the function $6 – 3x^2$, and when you set this expression equal to $0$ and simplify you get $x^2 = 2$ — an equation that has no solution in the rational numbers.

And the square root of two is nice compared to some of the other beasts that await you in calculus class. If you take the derivative of $10^x$, you get $10^x$ times the irrational number $\ln 10$. Or if you take the derivative of the sine of $x$ (where the angle $x$ is expressed in degrees), you get the sine of $x$ times the irrational number $\pi/180$. The first multiplier, $\ln 10$, whispers “You could make me disappear if only you’d use natural exponentials!” The second multiplier, $\pi/180$, whispers “And you could make me disappear if only you’d express angles in radians!”

But they’re trying to trick you. Accepting natural exponentials means accepting the irrational number $e$ as the One True Base, while accepting radians means worshipping at the altar of the Arch-Irrational, $\pi$. (I jest, of course.)

Why does calculus involve so many irrational numbers? A course in theoretical calculus (also called real analysis) can shed light on the issue. One digs underneath the function-concept to re-explore the number-concept and one finds that the properties of the number-line discussed in high school simply don’t suffice to get the calculus-motor up and running. One needs an extra ingredient in the fuel, called the completeness property of the reals. To paraphrase Obi-Wan Kenobe: The completeness property of the reals is what gives calculus its power. It surrounds us and penetrates us. It binds the number line together.

The real number system, with its plethora of nasty irrational numbers, possesses the completeness property; the tidier rational number system lacks it.

Using the completeness property we can prove the Intermediate Value Theorem: If a continuous function is positive somewhere and negative somewhere, then it’s got to be zero somewhere. Invoking this theorem, we can prove that $\sqrt{2}$ exists, since the continuous function $x^2 – 2$ is positive for some values of $x$x and negative for others.

Likewise, the completeness property lets us prove the Extreme Value Theorem: A continuous function on a (closed, bounded) interval must achieve its maximum value somewhere. So there must be a place at which the continuous function $6x – x^3$ achieves its maximum.

If we tried to do calculus using just rational numbers, neither the Intermediate Value Theorem nor the Extreme Value Theorem would be true: for, if we restrict x to rational values, $x^2 – 2$ is sometimes positive and sometimes negative but never zero, while $6x – x^3$ approaches but never achieves a maximum value. (See this Stack Exchange discussion to learn more about what goes wrong with calculus when you try to use only rational numbers.)

There are other theorems in theoretical calculus that work for the real number system but fail for the rational number system: the Mean Value Theorem, the Bolzano-Weierstrass Theorem, the Heine-Borel Theorem, etc.

And now I can get to the real point of this pitch. The theorems of the calculus that work for the reals but fail for the rationals, despite the very different claims they make, are all equivalent to each other! That is, if you’re dissatisfied with the rational number system and are looking to upgrade, and you go to the number-system store and say you want a number system that has this feature or that feature, most of the time the sales clerk will reply “Sounds like you want to buy the real numbers.” It’s a package deal; for the price of one feature, you get them all. (See this article to learn more about calculus theorems that are equivalent to the completeness property.)

My favorite theorem-secretly-equivalent-to-completeness is the Constant Value Theorem: it says that if the derivative of a function is $0$ everywhere, then the function must be constant. Obvious, right? But if you try do calculus using the rational numbers in place of the real numbers as your “everywhere”, the theorem fails. To see why, look at the function $f(x) = \operatorname{sign}(x^2 – 2)$: it’s $+1$ where $x^2 \gt 2$ and it’s $−1$ where $x^2 \lt 2$ (no fair asking “What about where $x^2 = 2$?” since we’re restricting to rationals).

In ordinary calculus the function $f(x)$ is discontinuous at $x = \sqrt{2}$, but if we’re restricting $x$ to be rational, the function is continuous throughout its domain. In fact, the function is differentiable with derivative $0$ throughout its domain. So the truth of the Constant Value Theorem depends on (and in fact is equivalent to) a subtle property of the real numbers that we don’t teach in most calculus classes but which makes calculus work.

To learn more about the Constant Value Theorem and why I love it, see my July 2019 Mathematical Enchantments essay, entitled My Favorite Theorem. I argue that the Constant Value Theorem underlies a principle of Newtonian physics so obvious that Newton didn’t bother to state it: if an object has velocity 0 for all time then it stays put. I also talk about the discrete analogue of the Constant Value Theorem, which is equivalent to the principle of mathematical induction.

The essay is a companion piece to a half-hour podcast episode in which I delve into the Constant Value Theorem and explain why mathematics is like a potato chip.

There’s some overlap, but the essay contains things that aren’t in the podcast and vice versa.

Sunil Singh – A Wormhole to Eigenvectors: “Cows”

Sunil is an author and speaker on the complexity, creativity, and curiosity of mathematical play! He works as a Mathematics Learning Specialist for Buzzmath. He’s @mathgarden on Twitter.

Several years back, there was quite a famous/infamous article written by Andrew Hacker in The New York Times regarding the state of algebra in the United States.

While the article was well written–with even some points that I agreed with–the key word, for me at least, which deflated a serious interest in the article was the word “necessary”.

The word “necessary” automatically conjures up ideas of practicality, and a pretty arid aesthetic of what algebra is, and in the end, what mathematics is–machinery that is dull and generally unimpressive for society. That is not what mathematics is for. It is, in the words of the great mathematician Francis Su, for human flourishing.

My first pitch was rooted in some quirky algebra. I am going to continue the theme here. This time I am going to take all of you on a whiplash tour of Peter Harrison’s “Cows in the Classroom”. We will go from some elementary adding and subtracting, and finally ending up, of all places with eigen vectors!

Back in the 80’s, Peter Harrison, wonderful math teacher in Toronto, Canada, created an absolutely charming template of cows and fields, that had various rules to navigate through–eventually ending up on a sturdy bridge between arithmetic and algebra.

It all started here.

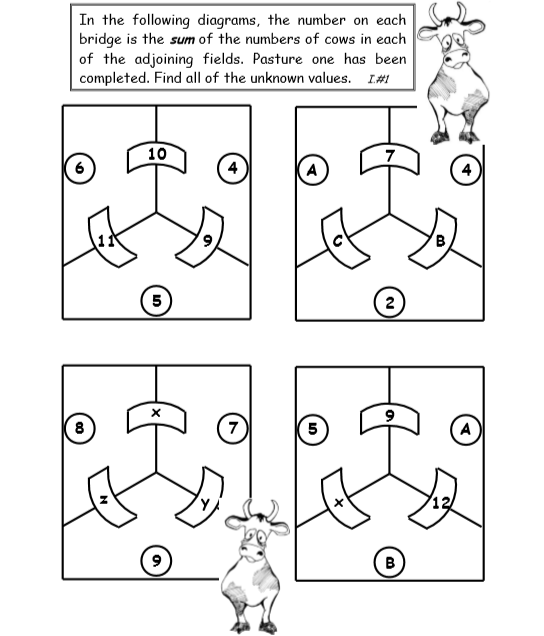
Pretty simple stuff. However, already students are somewhat amused by the disarming cow and the addition rule between the fields and bridges. Even in this straight-forward introductory puzzle–which could easily be done by early elementary kids–there is a subtle introduction of variables with different letters of the alphabet.

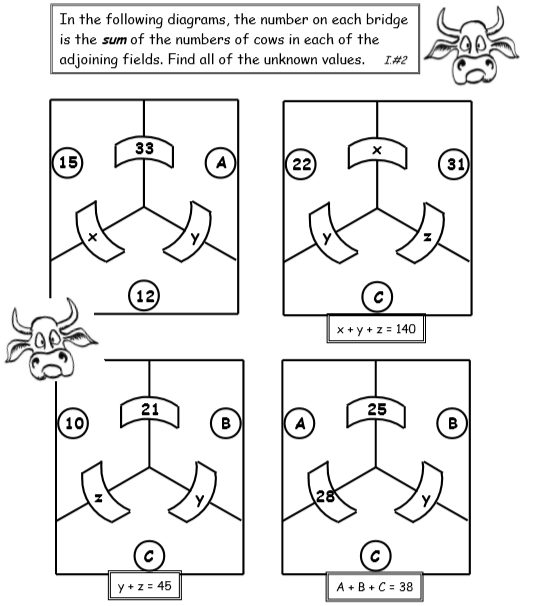
As you can see, these “addition” puzzles quickly escalate into at least thinking algebraically. There is no formal technique addressed or discussed. Just figuring out the unknowns through some process that is more natural and intuitive for the student.

One of the clever outcomes of the “Cows” are ideas about adding odds and evens.

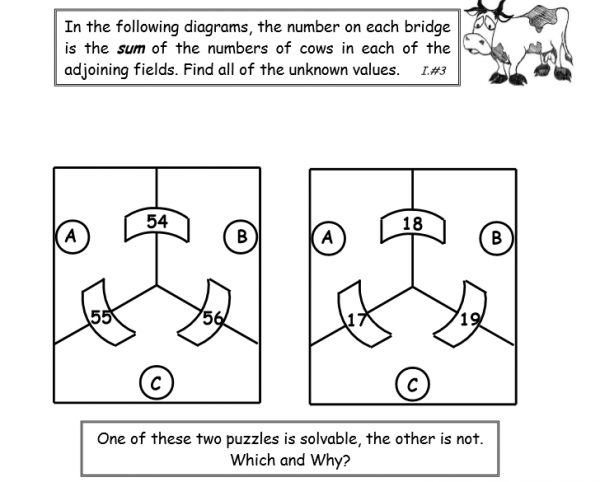
Even though we are only in the problems with “addition”, some pretty rich ideas that are fundamental to algebraic appreciation and neatly unpacked.

Finally, there is a question posed, that I believe is one of the great K to 12 math problems of all time. In that, that this problem poses mathematical interest/solution that is proportional to the mathematical maturity that is found at various age levels.

Students have to find single digit numbers(no repetition) that allows for a solution to the addition problem below. Again, bridges represent the sum of adjacent fields.

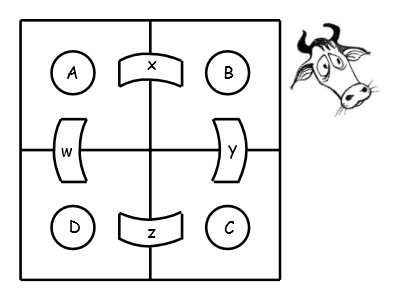
Early elementary kids might just use trial and error, and many would be able to get partial solutions–ie) if $A = 1$ and $B = 2$, the bridge $C$ has to be $3$.

Older kids might start to think about what numbers can’t be on the bridges, like 1 and 2. They might even incorporate some ideas about a general solution of odds and evens.

And, finally, high school students should use algebraic techniques that provide an elegant solution.

Peter Harrison had close to one hundred of these puzzles, that were meant to be done in some general order to increase the sophistication of thinking, moving to generalize arithmetic ideas–also known as algebra.

The last one is a doozy! It looks innocent enough, but quickly takes the resilient and curious student down a deep algebraic dive that lands them in the world of eigenvectors–of all places!

Here is the question:

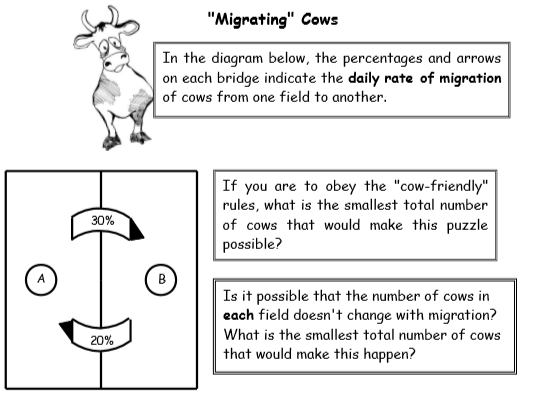
Take a deep breath! Here is the full solution — eigenvectors and all!

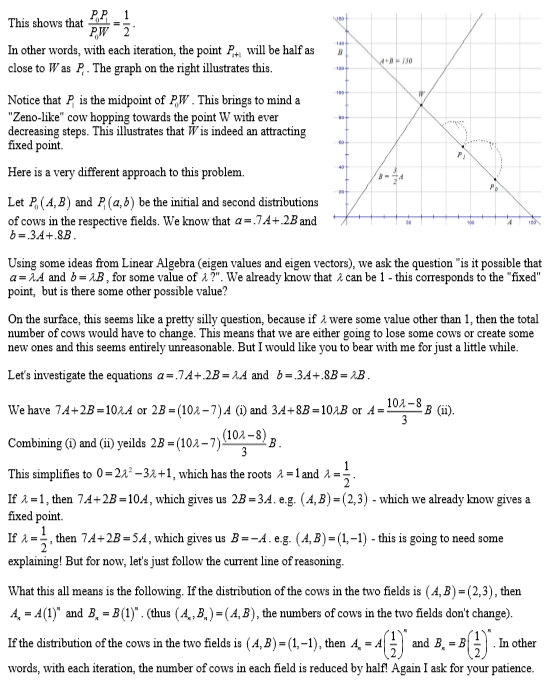
Let’s deep pause. One, to look back as where everything started. A simple, innocuous story about cows and fields rooted in simple addition–accessible to all. Two, while there are dozens of other Cows and Fields ideas that are absent in this narrative, the algebra that is developed is extraordinarily rich–probably well beyond the ability of most high school students.

Algebra is beautiful. However, any hope of all students seeing this kind of luminescence of mathematical reasoning has to be carefully introduced and curated.  

This kind of algebraic journey may not be necessary for the narrow goals of career objectives, but it surely is if we are to see mathematics as a language of poetry and creativity.

So, which bit of maths do you want to win? Vote now!

 Loading ...

The poll closes at 9am BST on the 16th. Whoever wins the most votes will win the match, and once the group stages are over, the number of wins will determine who goes through to the semi-final.

Come back tomorrow for our sixteenth match of the group stages, featuring Kyle Evans and Anna Haensch. Or check out the announcement post for your follow-along wall chart!