This is the seventh match in our group stage: from Group 3, it’s Sophie Carr up against Sunil Singh. The pitches are below, and at the end of this post there’s a poll where you can vote for your favourite bit of maths.
Take a look at both pitches, vote for the bit of maths that made you do the loudest “Aha!”, and if you know any more cool facts about either of the topics presented here, please write a comment below!
Sophie Carr – Bernoulli’s equation

Sophie Carr is the founder of Bays Consulting. Having grown up building Lego spaceships she studied aeronautical engineering before discovering Bayesian Belief Networks which has led to a career she loves – essentially make a living out of finding patterns. She prefers fresh coffee over tea, pears over apples and her favourite flower is the tulip. She’s @SophieBays on Twitter.
How on earth do you only choose three area of maths to talk about!? Well that was conundrum number one for me. To be clear, I’m not an academic (I’ve published less than a handful papers in my life), I don’t have an equation, theorem or anything named after me and didn’t grow up thinking I was that good at maths (in fact based on my year 9 exam results my maths teacher told my parents that I was unlikely to work in a maths related career).
That said, I’ve always had a love of aeroplanes and given that I’m really short sighted, becoming a pilot wasn’t a realistic option. Studying aeronautical engineering was possible – I could still work with aeroplanes, but only if I got better at maths. Since then, my career can be summed up as working on fun and exciting problems and puzzles, which has taken me from engineering, to applied maths and into the world of statistics. So that’s how I decided on my three topics and starting point is the equation that made me realise how maths, aeroplanes and engineering were all linked: Bernoulli’s equation. It’s also explains why shower curtains can be really annoying and stick to you; how you can direct objects in streams of air (from the polystyrene balls in the video through to the theory behind sailing boats) and even how to make cricket balls spin (pretty topical with the world cup going on at the moment). All from one equation that is really counter-intuitive. What’s not to like about that?!

The equation that sparked my interest was written by Daniel Bernoulli who came from a family of mathematicians (his dad was a famous mathematician and his brothers were also known for their ability in maths) and in 1738 he published what became one of his most famous books: Hydrodynamica. In this, Daniel explained how the pressure and velocity for a liquid are interlinked in a way that seems really contradictory. What Daniel showed was that as the velocity of the fluid increases then the pressure decreases – and not for just one fluid, but for all fluids that are moving steadily; (so for a given volume of fluid: there is no swirling or turbulence, like my local river below, and the velocity and density don’t change with time) are incompressible; (these fluids don’t see a change in their density even if there is a change in pressure) and any external viscous forces (in a fluid viscous forces are essentially sheer forces) being so small they can be ignored.

I still find the fact that for a fluid as pressure decreases, velocity increases as fascinating today as I did in the A Level Physics class when it completely captured my imagination (thanks Mr Brain – yes, that really was the name of my Physics teacher) But why does the equation work?
The way that Daniel Bernoulli wrote his equations is no longer the way we’re used to seeing them today. It was another famous mathematician, Euler, who presented them using notation we recognise today. There are two common ways of writing Bernoulli’s equation and below is the way I learnt at A Level:
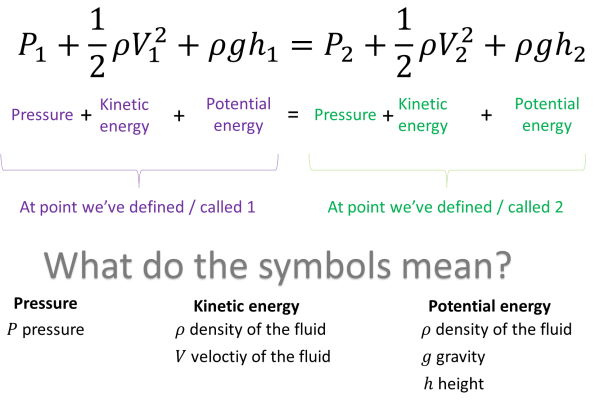
But what does this actually mean and why does pressure drop as velocity increases? Let’s put the equation in context. I’m going to select water as the fluid because people are used to seeing water flow and I’ll put the water in a pipe that’s got changing diameter. Then I’ll take two point at which the fluid flows past. Whilst we could name these points anything we want, for example Harriet and Mary, for the sake of keeping the equation short I’ll call them points 1 and 2. Lastly I need to think about a small volume of fluid, say the amount that flows past each point per second. This is important as we need to keep the volume of fluid flow constant throughout the pipe.
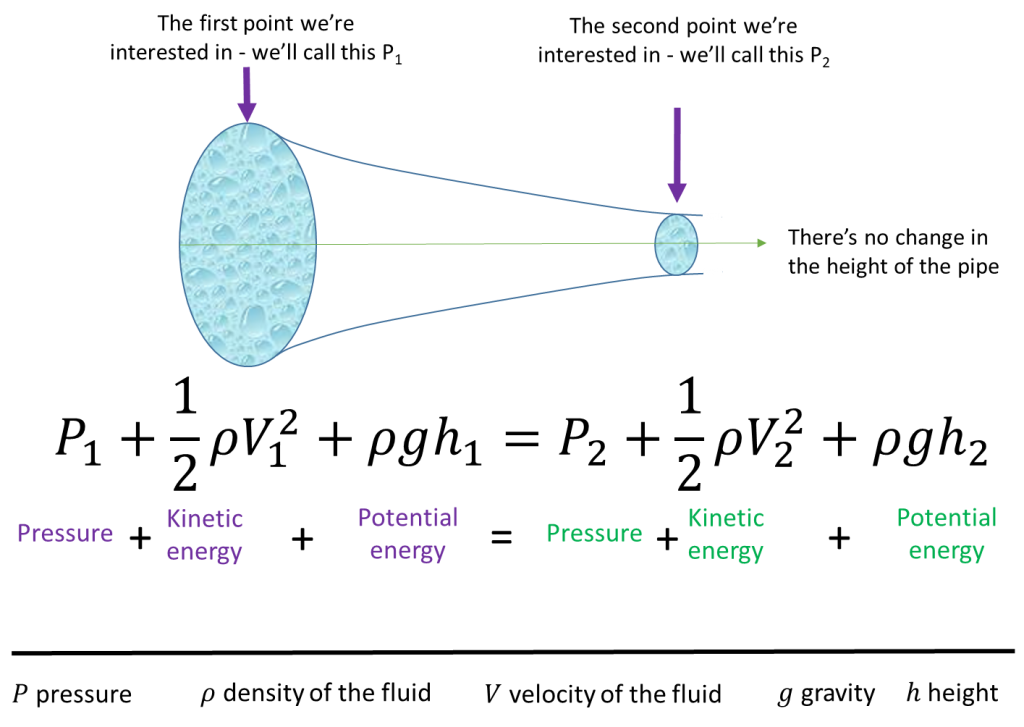
Now comes the great part because we can start to simplify the equation. As there is no change in the height of the pipe then there is no change in the potential energy between points one and two. This means we can remove the potential energy term from the equation which leaves:
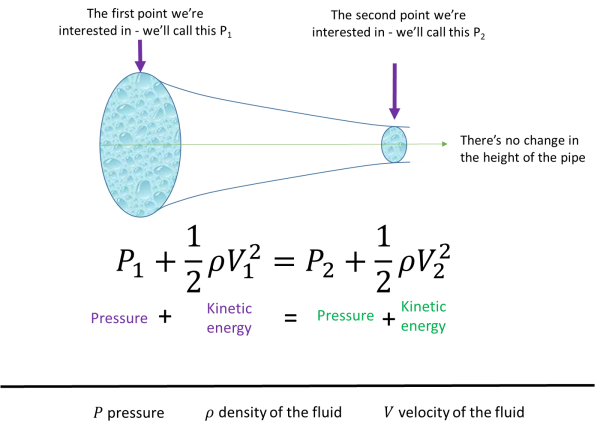
We know that the fluid is moving through the pipe and because of this, there is work being done on the fluid – simply put, there is a force acting on the fluid. Remember that we also need to keep the same volume of fluid moving through each point over a given time (and I set that as the volume of fluid per second)
At this point, it becomes easier I find to put numbers in. Lets say that at Point 1, 12 cm3 of water can pass in a second. We know that the same volume of water (12 cm3 ) needs to pass Point 2 in a second as well. However, at Point 2 the diameter of the pipe is smaller. The only way that the same volume of water can pass Point 2 in the same time as Point 1 is if the velocity of the water has increased.
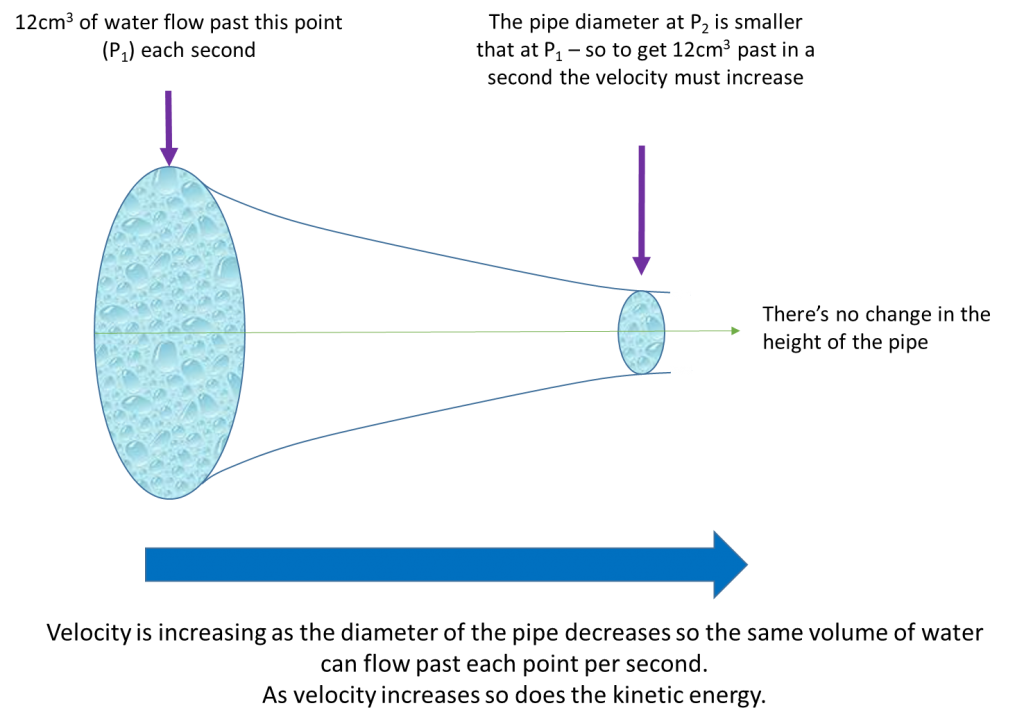
But, as the velocity increases so will the kinetic energy. So what happens to the pressure? The change in pressure can be explained by the conservation of energy: that is the total energy of a system is conserved. Energy can change form, but the overall amount stays the same. So for the total amount of energy at Point 1 to be the same as the total amount of energy at Point 2, if the kinetic energy at Point 2 has increased, this has to be balanced out by a decrease in the at the same point. Nifty. From the pressure difference we can start to understand the forces involved in moving the water forwards.
It’s not just in physical tubes and pipes where this phenomenon can be seen, in fact lots of us have had the really annoying experience of a shower curtain sticking to yourself. This is because the fast moving jet of water from the shower has lower pressure than the surrounding air, so it pulls the curtain towards you (no matter how much you try and bat it off). You can also see how you can have fun juggling balls in a fast moving stream of air from a Bernoulli blower (and a huge thank to the friendly and helpful staff at The IMA for letting me use their Bernoulli blower and explanation). The blower creates a fast moving jet of air, which has a lower pressure than the air around it – there is effectively a “pressure wall” that keeps the balls in the stream of air. This means that when you alter the angle of the jet, the balls move with it (after a bit of practice!) The video also shows another way of writing Bernoulli’s equation. However, for me, Bernoulli’s equation was my link into aeronautics, the start of learning about lift and a career I have adored.
Sunil Singh – The Correct Algebra Behind Mathematical Incorrectness

Sunil is an author and speaker on the complexity, creativity, and curiosity of mathematical play! He works as a Mathematics Learning Specialist for Buzzmath. He’s @mathgarden on Twitter.

Mathematics is such a vast universe of BIG ideas. And, many start there in trying to introduce people to the creative beauty of this subject. But, as alluded to in the Henry Miller quote, there is much magnificence and wonder in even the tiniest and unnoticeable crevices of math–which often lead to rabbit holes of deeper exploration.
One such “blade of grass” is in the somewhat obvious clumsiness of obtaining the correct answer to the question below
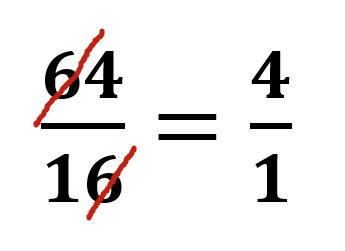
I came across this innocent looking problem through Peter Taylor of Queens University in Kingston, Canada. He has written/co-written some of the best high school math textbooks ever made!
Now on first glance, this just seems like a harmless coincidence, to maybe only shared as something mathematically comical–as opposed to mathematically curious. That was actually my first reaction when I first saw this. That this error was just a quirky coincidence, and no more investigation was needed to how the correctness was arrived by incorrectness.
But, what if I showed you another one of these double-digits mistakes?
\[ \require{cancel} \frac{\cancel{9}5}{1\cancel{9}} = \frac{5}{1} \]
Hmmm…another one? Are we chasing a rabbit here…, Alice?

Is there something going on here of significance? At this point, perhaps that is debatable. But, if we examine our “blade of grass” very closely, we will see that there is some neat algebra going on. And, sure you could use brute force to find the last two double digit occurrences of this mistake, but I think it is incumbent on us to use this innocent-looking peculiarity as a reminder to why building a bridge–an organic one–from arithmetic to algebra is one of the most important ideas in mathematics!
Let’s first start by rewriting it with a focus on place value.
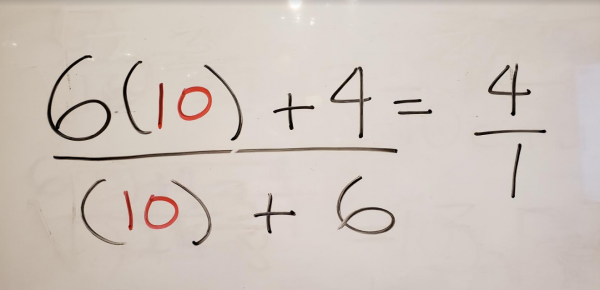
Now let’s assign all the numbers (except 10) some variables! After which, we can solve for $a$.
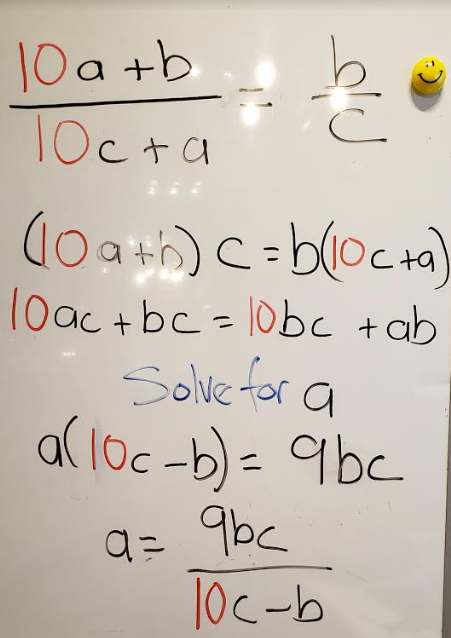
Now here $a$, $b$, and $c$ all have to be integers and be between 1 to 9. How do we approach this to cut down on trying all the possibilities for $b$ and $c$? Well, we should start by not selecting $b = c$, as that it will produce uninteresting results like $22/22$, $33/33$, etc.
Let’s start with $c = 1$:
\[ a = \frac{9b}{10-b} \]
We now get two possibilities, $b = 4$ and $b = 5$, giving us $a = 6$ and $a = 9$. This gives us the two situations that I shared with you at the beginning
$c = 2$
\[ a = \frac{18b}{20-b} \]
There is only one solution here: $b = 5$ and $a = 6$. This yields another result–a fraction, that when reduced is NOT a whole number! Brute force would have had a difficult time finding this one..
\[ \frac{\cancel{6}5}{2\cancel{6}} = \frac{5}{2} \]
There is no solution for $c = 3$
The last nugget to be plucked come from $c = 4$.
\[ a = \frac{36b}{40-b} \]
This yields one solution of $b = 8$ and $a = 9$. This gives us our final two-digit solution to incorrect simplifications that lead to correct answers.
\[ \frac{\cancel{9}8}{4\cancel{9}} = \frac{8}{4} \]
What is interesting is that there are other strange mathematical anomalies like this that occur with exponents and radicals–which would be even harder to find solutions with brute force. Reminding us once again, why to be able to see the arithmetic world through an algebraic lens gives us so much insight…and sometimes in the tiniest crevices of mathematics!
So, which bit of maths do you want to win? Vote now!
Match 7: Group 3 - Sophie Carr vs Sunil Singh
- Sophie Carr with Bernoulli's equation (69%, 192 Votes)
- Sunil Singh with correct errors (31%, 86 Votes)
Total Voters: 278
This poll is closed.
The poll closes at 9am BST on the 8th. Whoever wins the most votes will win the match, and once the group stages are over, the number of wins will determine who goes through to the semi-final.
Come back tomorrow for our eighth match of the group stages, featuring Becky Warren and Anna Haensch. Or check out the announcement post for your follow-along wall chart!
The closure date is incorrect
Oops! Fixed. Thanks for pointing it out.
In Sunil Singh’s pitch, \[\frac{9b}{10b-1}\] should be \[\frac{9b}{10-b}\].
My fault. Fixed.