This is the nineteenth match in our group stage, but there’s been a change to the schedule: from Group 3, it would’ve been Vicky Neale against Sunil Singh. Unfortunately, some grade A eejits have made a situation where Sunil can’t concentrate on the competition any more, so he’s had to pull out.

Vicky had already written her pitch, and there’s no way we’d keep it from you, so we present it below. I’ve also added a bit of fun maths from my own collection to make up the slack. There’s no voting today, and it’ll count as a win for Vicky.

Take a look at both pitches, and if you know any more cool facts about either of the topics presented here, please write a comment below!

Vicky Neale – Euclid’s algorithm

Vicky Neale is the Whitehead Lecturer at the Mathematical Institute and Balliol College, University of Oxford, which means her job is to be enthusiastic about mathematics with undergraduates, school students, and anyone else she can find.  She is the author of Closing the Gap: the quest to understand prime numbers. She’s @VickyMaths1729 on Twitter.

This is one of my all-time favourite mathematical ideas. I hope you enjoy my knitted version, complete with inquisitive baby hedgehogs.

The old cliche is that a picture is worth a thousand words. This particular picture is worth 6 equations. Specifically, it captures the system of equations

\begin{align}
192 &= 1 \times 111 + 81 \\
111 &= 1 \times 81 + 30 \\
81 &= 2 \times 30 + 21 \\
30 &= 1 \times 21 + 9 \\
21 &= 2 \times 9 + 3 \\
9 &= 3 \times 3
\end{align}

In fact it’s even better than that: it represents a family of infinitely many systems of 6 equations! For example, it also captures the system

\begin{align}
64 &= 1 \times 37 + 27 \\
37 &= 1 \times 27 + 10 \\
27 &= 2 \times 10 + 7 \\
10 &= 1 \times 7 + 3 \\
7 &= 2 \times 3 + 1 \\
3 &= 3 \times 1
\end{align}

and

\begin{align}
256 &= 1 \times 148 + 108 \\
148 &= 1 \times 108 + 40 \\
108 &= 2 \times 40 + 28 \\
40 &= 1 \times 28 + 12 \\
28 &= 2 \times 12 + 4 \\
12 &= 3 \times 4 \text{.}
\end{align}

The first system of equations implements Euclid’s algorithm to show that the highest common factor of 192 and 111 is 3. The second shows that the highest common factor of 64 and 37 is 1. The third shows that the highest common factor of 256 and 148 is 4. The picture shows all of these, all at once!

You can experiment with an interactive version of the diagram, where you can change the two input parameters, using the NRICH resource Picture this!. I’ve used this interactive version with lots of groups of students, who have used it to discover Euclid’s algorithm for themselves. With care, you can use the diagrammatic version to see why Euclid’s algorithm gives the highest common factor of two numbers. (If you’re not familiar with Euclid’s algorithm, I hope you might enjoy experimenting with the interactive version to explore it for yourself — but of course Google will give you lots of resources relating to it.)

One thing I find intriguing about this diagram is that it has to be a specific diagram relating to specific numbers — I can’t knit a diagram with side lengths a and b and an unknown number of steps — but nonetheless it is possible to see the full generality within the specific diagram. Arguably it is easier to see what is going on in general with a specific example than it would be with a system of equations such as

\begin{align}
a &= q_1 b + r_1 \\
b &= q_2 r_1 + r_2 \\
r_1 &= q_3 r_2 + r_3 \\
\ldots \\
r_{n-1} &= q_{n+1} r_n
\end{align}

Why knit it? Well, why not?! Also, I enjoyed the idea of knitting an algorithm, because knitting patterns are themselves algorithms. One definition of an algorithm might be that it is a sequence of precise instructions, possibly repeating, that will solve a problem or produce a particular output in a finite time. (The word “algorithm” comes from the name of the mathematician Abu Ja’far Muhammad ibn Musa Al-Khwarizmi. So I guess the word “algorithm” is hundreds of years more modern than Euclid‘s algorithm.) I think that a knitting pattern fulfils that definition. To knit Euclid’s algorithm, I followed a knitting algorithm.

One more comment on the knitting. Euclid’s algorithm is really efficient. This is brilliant in mathematical contexts and for applications, and a pain for knitting. To capture some generality in my diagram, I needed to have multiple squares of some sizes (multiple squares of the same colour), and also several different sizes (squares of different colours). The diagram with one square of each size is interesting, but a very special case relating to Fibonacci numbers, as we can see in this screenshot from the NRICH interactive version.

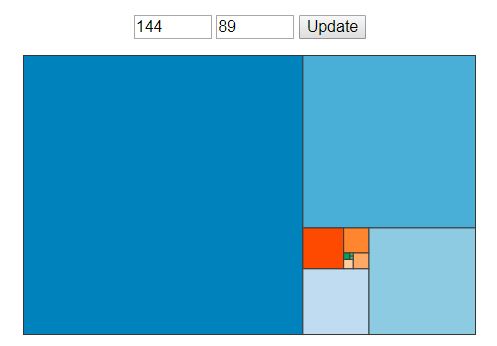
So I needed some repeated squares of the same colour, and some squares of different colours. I also couldn’t start too small, because of practical knitting constraints. In the end I went for 3 × 3 as the smallest I could sensibly make (this square is in fact 3 stitches wide and 5 rows, because knitting stitches are not themselves square). But then the rectangle grew significantly, because Euclid’s algorithm is so annoyingly efficient! The largest square is 111 stitches wide, and it look me a very long time to knit it…

Sunil Singh Christian Lawson-Perfect – The largest small hexagon

Sunil is an author and speaker on the complexity, creativity, and curiosity of mathematical play! He works as a Mathematics Learning Specialist for Buzzmath. He’s @mathgarden on Twitter.

Sunil has had to drop out of the competition, due to some extremely unhelpful people. Instead, here’s a bit from my collection.

I’m going to make a statement below, in an authoritative fashion. It’ll look quite innocuous, and in any other context you’d probably accept it without much thought.

The regular $n$-gon has the greatest ratio of area to diameter of any $n$-sided polygon.

That’s not true! It totally looks like it is, but it’s not.

It’s at least half true: for odd $n$, the regular $n$-gon is biggest, but that’s not necessarily the case for even $n$. When $n$ is even, there’s some wobbly fella who’s just that bit bigger than the factory-fresh regular model. As a big wobbly fella, I can get on board with this fact.

A paper by Ron Graham titled The Largest Small Hexagon shows that the biggest six-sided shape with diameter 1 is this beastie:

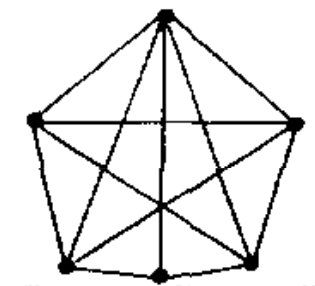
And it’s unique. Isn’t that interesting?

Its area, approximately 0.674981, or 3.92% larger than the regular hexagon, is a solution to this irreducible polynomial over the integers:

\[ Q(x) = 4096x^{10} + 8192x^9 – 3008x^8 -30848x^7 + 20156x^6 + 146496x^5 – 221360x^4 + 1232x^3 + 144464x^2 – 78488x + 11993 \]

How was it found? Graham’s paper gives a breezy but dense proof. I won’t go into it, but I can’t resist noting that it makes use of linear thrackleation. What a fun word!

So, there you go! Again, there’s no voting today, and this’ll count as a win for Vicky.

Come back tomorrow for our twentieth match of the group stages, featuring Colin Beveridge and Anna Haensch. Or check out the announcement post for your follow-along wall chart!