This is the eighth match in our group stage: from Group 4, it’s Becky Warren up against Anna Haensch. The pitches are below, and at the end of this post there’s a poll where you can vote for your favourite bit of maths.

Take a look at both pitches, vote for the bit of maths that made you do the loudest “Aha!”, and if you know any more cool facts about either of the topics presented here, please write a comment below!

Becky Warren – Sonobe shapes

Becky Warren is a freelance maths educator and communicator. She loves neat mathematical puzzles, mathematical art and origami. Her occasionally updated blog is called Lines Curves Spirals. She’s @becky_k_warren on Twitter, where she loves joining in the #beingmathematical chat on Thursdays.

The Sonobe module is a great introduction into the world of modular origami. The module itself is quite straightforward but can be used in a huge number of creative ways. If you haven’t tried making Sonobe modules before you might like to have a go with these video instructions or a diagram.

Here are some models I made with 3, 6, 12 and 30 modules.

Most instructions describe the larger models as an icosahedron and an octahedron. To be more precise these are a stellated icosahedron and a stellated octahedron. A stellation of a polyhedron is created when a face of the polyhedron is extended; in this case a pyramid is formed on each original face.

It is worth noting that the number of modules needed to create these shapes corresponds to the number of edges of the original shape before it was stellated. The icosahedron has 30 edges and the stellated icosahedron model has 30 modules, and octahedron has 12 edges and the stellated octahedron model needs 12 modules.

This next model looks like a cube. However by following the pattern above and noting that it is made from 6 modules I would like to suggest that it is in fact a stellated tetrahedron.

I love the stellation of the tetrahedron. By changing the amount of stellation on the tetrahedron you can find a perfect point where the faces of the stellations are exactly aligned, the pyramids are made of right-angled triangles and you do in fact have a cube. Beautiful!

Now let us look at our smallest model.

What shape might this be? This model was made of 3 modules. If, as before, this corresponds to the number of edges the initial shape had before it was stellated, we have to conclude that it is a triangle that has been stellated on both sides!

There is another shape that can be made from Sonobe modules. This one needs 12 modules and looks like a cube.

I think that this model is actually a stellated cube that has a stellation of zero. This makes sense when you consider that each stellation on the other models is made from three isosceles right-angled triangles. A cube has square faces and when you put four isosceles right-angled triangles together they will not make a pyramid, and the face will remain flat.

For completeness I am going to leave you with a stellated octahedron and a stellated icosahedron to play with. What happens when the stellations align on these models?

Sonobe shapes are only one of a huge variety of modular origami models. Many other models have their own fascinating mathematical structure too. Have a play. What other shapes can you make? What mathematics can you find?

Anna Haensch – How to Become an Oligarch

Anna Haensch is a professor at Duquesne University in Pittsburgh, PA.  She’s a number theorist, math blogger, and sometimes podcaster. She’s @extremefriday on Twitter.

The 2019 report from Oxfam International determined that 26 people hold as much wealth as the 3.8 billion people in the poorer half of the population. And if that’s not enough to get you in a lather, consider this: in 2019 Jeff Bezos’ wealth grew to $112 billion, which, to put things in perspective, means that just 1% of Mr. Two-Day-Prime-Shipping’s wealth is the same as the entire health budget for Ethiopia’s population of 1.5 million. He, and his 25 super rich friends, are what we would term “oligarchs.”

These are the super rich people whose extremely condensed wealth is so vast that they seem almost untouchable. And mathematically, there’s a reason these people exist and there’s a reason we can’t seem to catch up to them. Rather than try to understand the whole complicated web of the economy, let’s consider how wealth changes hands in one-on-one transactions in a super simplified model. You have two agents, one of whom is poorer. To decide who profits from any given transaction, we can flip a fair coin. And to decide how much wealth will change hands, we will always take some percentage of the poorer person’s wealth. This setup makes sense, if we take into account the innate aversion humans have to “risking it all” but ignore for a moment the various extrinsics that make the wealthy people more likely to “win.” In this setup, if we consider many small transactions over time, the model has been shown to have a Boltzmann equation which reduces to a Fokker-Planck equation. So kind of like studying the conservation of energy in a system when particles are bumping into each other, we can model the conservation of wealth in a system where pairs of people are constantly swapping money.

With this model, it was shown by Boghosian et al, that over time a complete oligarchy will emerge, regardless of initial conditions. Which is not so great, unless you’re an oligarch.

Here I looked at what happened over 10,000 transactions between three agents, when I choose transaction pairings at random and gave the winner just 2% of the poorer agent’s total wealth. You can download my Sage code and try it on your own!

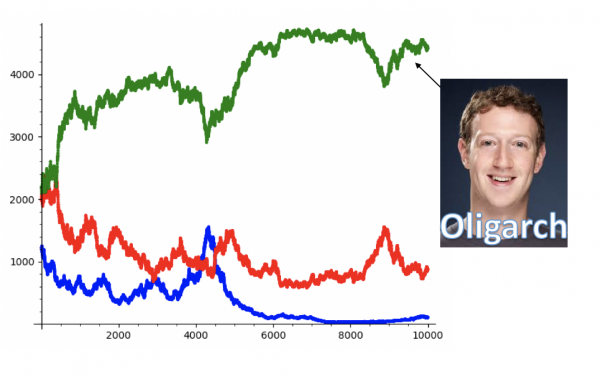
But the situation is actually worse than this, since we are ignoring the fact that well-off people are more likely to win for a variety of reasons. By factoring the advantage of the wealthy into the model we are really biasing the coin flip towards the rich guy. So let’s suppose the richer person wins 60% of the time – and be advised, I’m just making these numbers up right now for the purpose of illustration. Then we reach reach an oligarchy even faster.

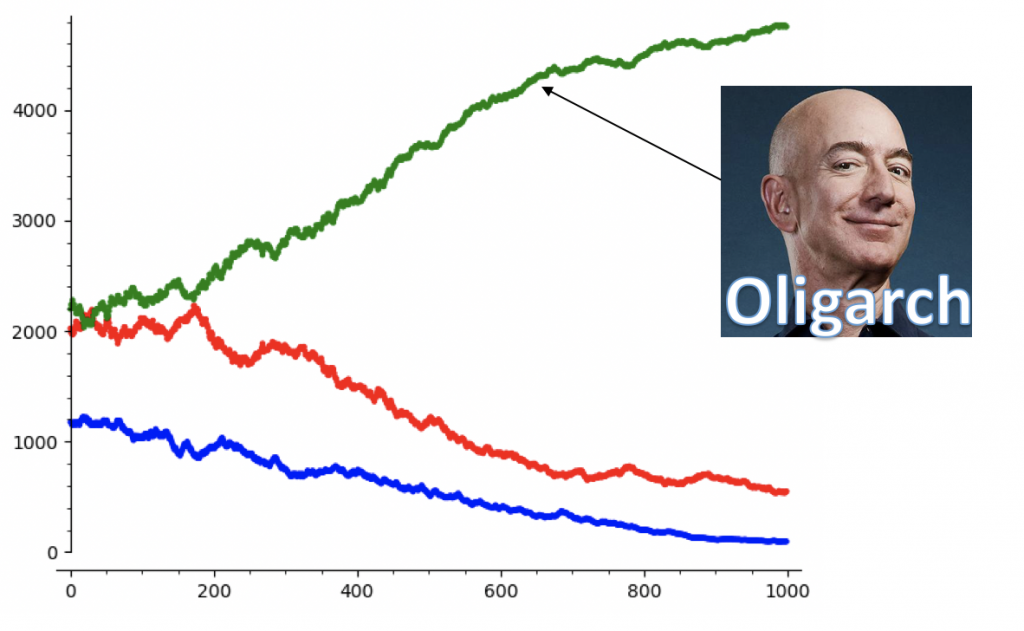
Which again, is pretty bad, unless you’re an oligarch.

It looks like the one good way to stop our inevitable descent into extreme inequality, is to redistribute some of that wealth, and that’s what some mathematicians and economists have been working on modeling over the last several years. This can be introduced by applying a successive dragging-back-towards-the-mean after each transaction. Work of Boghosian et al develop a two parameter model of wealth distribution, accounting for the wealth advantage bias factor and this redistribution factor. Their model hews to within 1% of US and European wealth distribution over the last 30-ish years. If you’re interested in reading more of the details, there are serval interesting papers from Boghosian et al. about mathematical models for wealth redistribution.

So, which bit of maths do you want to win? Vote now!

 Loading ...

The poll closes at 9am BST on the 9th. Whoever wins the most votes will win the match, and once the group stages are over, the number of wins will determine who goes through to the semi-final.

Come back tomorrow for our ninth match of the group stages, featuring Lucy Rycroft-Smith and Grant Sanderson. Or check out the announcement post for your follow-along wall chart!