This is the twentieth match in our group stage: from Group 4, it’s Colin Beveridge up against Anna Haensch. The pitches are below, and at the end of this post there’s a poll where you can vote for your favourite bit of maths.
Take a look at both pitches, vote for the bit of maths that made you do the loudest “Aha!”, and if you know any more cool facts about either of the topics presented here, please write a comment below!
Colin Beveridge – Left as an Exercise: Pascal’s Triangle

Colin Beveridge is the author of two popular maths books and several unpopular ones, all of which are available wherever good books are sold. He writes the Flying Colours Maths blog, brings up two children with his partner, and has his eyes on a triathlon in the distant future. He has an equation named after him and once set himself on fire making a sandwich. He’s @icecolbeveridge on Twitter.
I’ve loved Pascal’s Triangle since I was old enough to add numbers up. This video looks at what happens if you extend the triangle into negative-numbered rows.
In it, I promise to link to some of my favourite things about it that I don’t mention:
- Singmaster’s conjecture
- The central column of Pascal’s triangle gives the coefficients of $ \left( 1 – 4x^2 \right)^{-1/2} $: OEIS sequence A000984
- You can calculate the parity of any element of Pascal’s triangle using bitwise arithmetic: Lucas’s theorem
- The number of presents given by my true love on the twelve days of Christmas is 14 C 3. The proof is left as an exercise.
Anna Haensch – Piece of cake!

Anna Haensch is a professor at Duquesne University in Pittsburgh, PA. She’s a number theorist, math blogger, and sometimes podcaster. She’s @extremefriday on Twitter.
Everybody loves cake. And whether you’re a frosting on top or frosting on the bottom type, everybody’s also got that perfect size to frosting ratio they desire. Sadly, bakeries are in the habit of slicing cakes uniformly, which is not only boring, but I’d argue that it’s also unprofitable. It would be better if you could get the maximal number of slices out of each cake, while still allowing customers to have some voice in the matter of size and frosting content. Hear me out on this one.
Let’s reduce this problem by one dimension, and suppose that instead of cake, we have a cookie, and suppose you commit to cutting this baked good 4 times. Slice, slice, slice, slice. Then a couple of things can happen. You might draw every slice through the center line, giving you a perfect 8 slices, but you might miss your mark a bit, getting 9 slices or even 11!
This is the crux of the Lazy Caterer’s problem, which asks for the maximal number of slices that can be obtained by slicing a tasty round thing a fixed number of times. The Lazy Caterer’s Sequence is the sequence
\[ 1, 2, 4, 7, 11, 16, 22, 29, 37, 46, 56, 67, 79, \ldots \]
whose $n^\text{th}$ term corresponds to the maximum number of slices that can be obtained with $n$ cuts. Each term in the sequence can also be arrived at by a closed formula, namely,
\[ a_{n}=\left(n\atop 2\right)+\left(n\atop 1\right)+\left(n\atop 0\right) = \frac{n^2+n+2}{2}. \]
Visually, the lazy caterer’s sequence can be seen in the picture below.
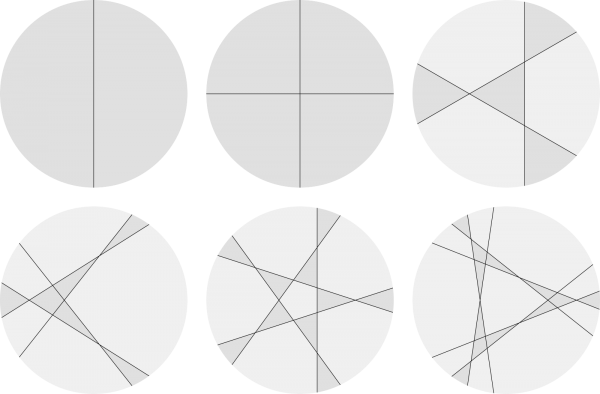
Unsurprisingly, this also has a higher dimensional analogue called Cake Numbers. These are the maximal values obtained by cutting slicing a cake $n$ times. So if your cake is square, this would look something like planes slicing thorough a cube.
The cake number also has a closed form, namely, the $n^\text{th}$ cake number is given by
\[ c_n = \left(n\atop 3\right)+\left(n\atop 2\right)+\left(n\atop 1\right)+\left(n\atop 0\right) = \frac{1}{6}(n^3+5n+6) \]
By shooting for this number of slices, you can always guarantee the highest volume of sales from each torte, and therefore I propose this as the best way to have your cake, and eat it — in a maximal number of slices — too!
So, which bit of maths do you want to win? Vote now!
Match 20: Group 4 - Colin Beveridge vs Anna Haensch
- Anna with lazy caterers (54%, 74 Votes)
- Colin with Pascal's triangle (46%, 62 Votes)
Total Voters: 136
This poll is closed.
The poll closes at 9am BST on the 21st. Whoever wins the most votes will win the match, and once the group stages are over, the number of wins will determine who goes through to the semi-final.
Come back tomorrow for our twenty-first match of the group stages, featuring Alex Corner and Grant Sanderson. Or check out the announcement post for your follow-along wall chart!