Group theory is a strange and wonderful area of study in mathematics, with plenty of key ideas and core concepts for one to wrap their algebra-hungry head around. But how do you introduce these algebraic constructs to beginners in a fun and engaging manner, whilst simultaneously providing a thoughtful read for the experts? This is exactly what mathematician and computer scientist Alex Berke accomplishes with her mathematical colouring book Beautiful Symmetry and its innovative group colouring concept.

Old Ideas Reimagined

Alex sets out to show mathematics is not just numbers, but can in fact assume many different forms, an idea not typically seen in traditional education. Berke gently eases the reader into these abstract ideas by utilizing symmetry groups as an entry point. Giving the reader the opportunity to first get to grips with different types of symmetries, Alex uses this to gradually build ideas in group theory.

The book introduces key concepts such as group axioms and generators throughout, with plenty of charming examples accompanying them, keeping the reader enthused every step of the way. Among the topics covered are Frieze, Dihedral, and Wallpaper groups, all accompanied with elegant illustrations.

Colouring challenges break up the straight-to-the-point text, providing opportunity to reinforce learning whilst enjoying the simple pleasure of colouring. It allows the reader to experiment and play with the examples, in order to encourage independent learning. The printed edition is accompanied by an interactive web copy with animations demonstrating the written ideas. This approach allows the reader to develop a much greater intuition on the ideas being presented before them.

Who is ‘Beautiful Symmetry’ for?

Having already spent years with group theory, I did worry going in that this may be a retelling of ideas I have already seen. In fact, for those with extensive knowledge in the field, the first quarter of the book may incite some tedium as it introduces the barebones basics. However, the book does not intend itself to be a comprehensive textbook; it instead offers a new and interesting insight into the field of study, presenting an alternative point of view to get one enthused in the idea of a group.

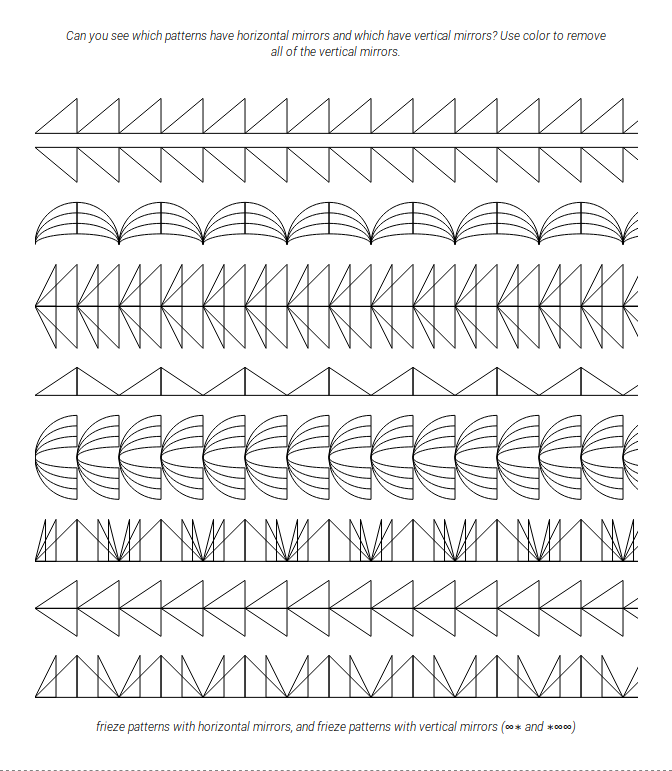
Once the basics are out of the way, the pages open up into a variety of new ideas where I even learned some concepts I had not previously encountered, much to my surprise. This diagrammatical nature Alex takes is what allows this book to be so accessible to all levels of mathematical minds.

Is this one to grab?

This question is difficult to answer really, as it all depends on context. For someone who seeks to educate themselves on group theory for academic purposes, this is not the way to do it. It instead can complement one’s studies. What I will say is for those familiar with the field, please do not be discouraged by the gradual approach, there is plenty here to keep your mathematical brain engaged. And, for those unfamiliar with the idea of a group or even mathematics beyond secondary school, please do not be daunted, as there is plenty here to keep you entertained.

So overall, yes, this book would quite comfortably make an interesting and colourful addition to one’s bookshelf.

You can read Beautiful Symmetry online, or buy the physical edition from MIT Press.