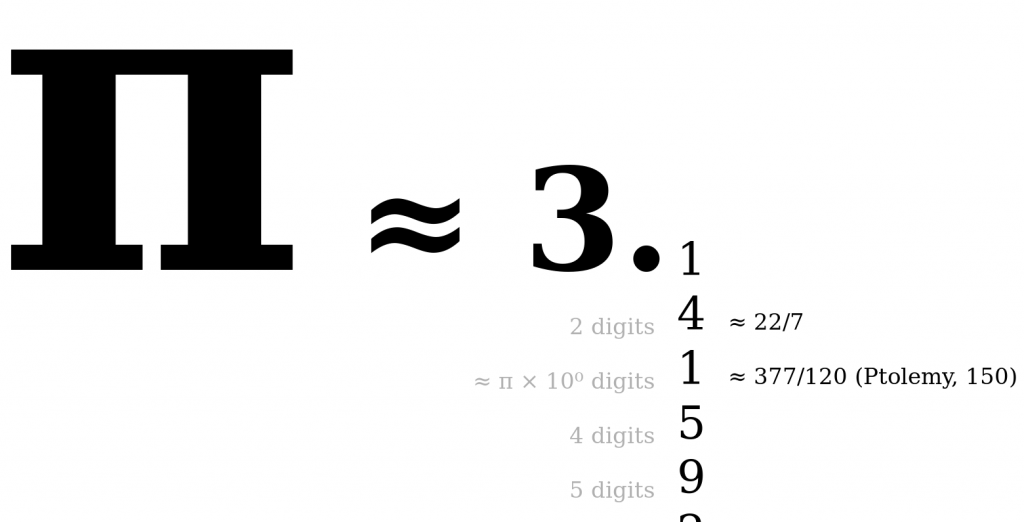Hexaflexagons are great.
If you haven’t seen one before, you’re about to have a lovely time.
If you have seen them before, the reason I’m writing about them is that I’ve made a webpage that helps you create a template for a hexaflexagon with your choice of picture on each of the three faces.
Here’s a round-up of news stories from January 2023.
The British Prime Minister Rishi Sunak has announced that all students will study maths to age 18. The response has been varied, with commentators from both within mathematics and from non-mathematical backgrounds weighing in (with varying degrees of nuance).
However, this isn’t planned to happen soon – only to start the work to introduce this during this Parliament, with actual implementation to happen at an unspecified point in the future.
It’s worth noting that there is a shortage of maths teachers, with nearly half of schools currently using non-specialist maths teachers, according to the TES.
The fact this might make maths a political football is a bit of a problem – the opposition Labour party say “they’ve nothing to offer the country except double maths”. (As much as we love maths, we’ll agree there are more important things to worry about at the moment).
The Chrome browser, and eventually other browsers built on it such as Edge and Opera, can now render MathML without any additional libraries as of version 109. Chrome briefly had some support for MathML, which was removed in 2013 due to lack of interest from Google. The developers who were working on it have kept plugging away, funded by the open source software consultancy Igalia.
Until now, the only reliable way to display mathematical notation on the web has been to use a JavaScript library such as MathJax or KaTeX, which do all the work of laying out symbols using generic HTML elements.
Now, you can just put MathML code in a page and expect most browsers to display it, like this:
There’s still a need for MathJax and the like: writing MathML code is no fun, so they’re still useful for translating LaTeX code, and MathJax adds a range of annotations that help with accessibility. But this is a step towards mathematical notation being much easier to work with on the web!
The US National Academies have released a series of posters “Illustrating the impact of the mathematical sciences”.
CLP’s place of work still has some Millennium Maths Project posters clinging on to the walls, older than almost all of the students, so maybe it’s time for a refresh! (via Terence Tao)
Tim Austin is the new Regius professor mathematics at Warwick. (via Warwick Mathematics Institute)
A bit of bureaucracy news: the Council for the Mathematical Sciences, comprising the five learned societies for maths and stats in the UK, is creating a new Academy for the Mathematical Sciences. It looks like the societies for the different sub-disciplines have acknowledged they need to work together, though this gives off a “now you have n+1 standards” smell. They’ve got a nice logo, though.
The Financial Times style guide changed so that ‘data’ is always singular, pragmatically following common usage. FT writer Alan Beattie said it best: “For anyone opposed, I’d like to know what your agendum is.“
The London Mathematical Society will hold a ceremony in London on 22nd March to officially award the Christopher Zeeman medal to the 2020 and 2022 medallists, Matt Parker and Simon Singh.
The ICMS in Edinburhgh has launched a “Maths for Humanity” initiative, which will be “devoted to education, research, and scholarly exchange having direct relevance to the ways in which mathematics, broadly construed, can contribute to the betterment of humanity.” (via Terence Tao)
Yuri Marin has died. The Max Planck Institute has posted an obituary describing his life’s work. One of his PhD students, Arend Bayer, collected some memories in a Mastodon thread.
William ‘Bill’ Lawvere has died. There is a page on the nLab describing his life’s work.
Group theory is a strange and wonderful area of study in mathematics, with plenty of key ideas and core concepts for one to wrap their algebra-hungry head around. But how do you introduce these algebraic constructs to beginners in a fun and engaging manner, whilst simultaneously providing a thoughtful read for the experts? This is exactly what mathematician and computer scientist Alex Berke accomplishes with her mathematical colouring book Beautiful Symmetry and its innovative group colouring concept.
Recently someone on Twitter, and then two people on US cable news, said that Michael Bloomberg could have used the \$500 million he spent on his presidential campaign to give everyone in the USA \$1 million. This caused quite a fuss.
In short, someone divided 500 by 327, saw that the answer was bigger than 1 and the units were “millions”, and concluded that the money could instead have been distributed to give everyone \$1 million.
That’s an easy mistake to make for someone writing a tweet, but the kind of error that should have made someone think “does that make sense?” before planning a segment on TV news about it.
It’s raised a couple of interesting questions, though:
I realised that all the data I need is freely available on the internet, so I made a website to do the calculations for you:
make-it-rain-bloomberg.glitch.me
It asks you how much money you’ve got, then for every power of 10 dollars, it tells you where in the USA you could give every resident that much.
To give you an idea of how far the net worths of people like Michael Bloomberg could go, it’s got a list of shortcuts for billionaires. Appropriately, I got that data from Bloomberg’s own website. Bloomberg himself was mysteriously missing from the list, so I got his net worth from Google and added it in myself.
The most unexpected thing for me was seeing how much money these people would have left over after giving everyone in the USA \$100. They’d still be enormously, unimaginably rich!
I’ll describe a few of the fiddly details of the implementation now. At first the “how much money have you got?” input was a text field, but I realised it’d be much better to have a slider that you can swing from \$1 all the way up to \$1 trillion. It’s a logarithmic scale, so powers of 10 are equally spaced.
I got data on the populations of US cities and states from data.census.gov.
Working out which amounts and places to show you wasn’t completely straightforward. I thought it’d be easiest to fix the amounts given away to a power of 10 per person, and to find places where the population meant that the amount left over would be as small as possible. To do that, my code works through the list of places in ascending order of population, and stops at the last place whose population is big enough to give everyone at least the target amount.
I enjoyed making this tool, and I hope it helps somebody get a better feel for what these big numbers mean.
Spread your wealth at make-it-rain-bloomberg.glitch.me.
You know what’s fun? Typesetting mathematics! Glad you agree, because here’s a game that puts the fun in ‘underfilled hbox’.
In TeXnique, you’re shown a typeset bit of mathematical notation, and have to frantically type LaTeX to reproduce it. You get three minutes, and you’re awarded points when you produce something that’s a pixel-perfect replica of the original. Think Typing of the Dead crossed with The Art of Computer Programming.
When I first saw this I rolled my eyes, but now my high score is 68 and I don’t know why I keep going back to it.
The formulas are largely well-known snippets of notation, so you might find some of them coming out through muscle memory, but if a symbol shows up that you can’t remember the macro for, there’s always the brilliant Detexify tool.
Play: texnique.xyz by Akshay Ravikumar.
This is a guest post from Philipp Legner, the creator of Mathigon – an interactive maths education platform.
Every year, thousands of students around the world ask themselves why they have to learn mathematics. Calculators can do long division. You can look up the quadratic formula on the internet. And when will you ever need calculus in everyday life? It seems like they have a point.
In fact, the maths curriculum has not changed significantly in the last 50 years. Its primary focus is on memorising rules and procedures which can be used to solve standardised exam questions. I created Mathigon because I strongly believe we need to change this – not only to make mathematics more enjoyable for students, but also to teach different skills that are much more useful in life: problem-solving, abstraction, logical reasoning, creativity, and curiosity.
It’s π eve, and I’ve had a silly idea: I’m going to take the ridiculous website I made to show all the digits of π, and stream it scrolling indefinitely through them over the internet.
Starting at midnight GMT on 2019-03-14, the stream below will start scrolling down through the digits of π:
I had this idea this morning, and it’s running on my desktop PC which I’ll be away from until 8am tomorrow, so I won’t be surprised if something goes wrong.
But if it doesn’t: hooray!