Welcome to what has become by default the sporting event of the year! The Big Math-Off is running a little bit earlier this year, to keep us entertained while we’re stuck indoors.

Because it’s unclear how long the lock-down will last, and nobody knows what’s coming one day to the next, this year’s Math-Off is a much less structured affair. Anyone can enter, and every two days for as long as we can we’ll pick two pitches off the queue and pit them against each other. Nobody gets knocked out, the votes don’t mean anything, and we’ll see lots of different bits of maths. It’s the ideal Math-Off!

You can still submit pitches, by the way: instructions are in the announcement post.

So, let’s begin! Here’s the first pair of pitches.

Andrew Stacey – Absolutely Marvellous

Andrew Stacey writes about maths at loopspace.mathforge.org.

For my first Big Math-Off entry, I’d like you to consider a very important question that I’m sure all Mathematicians ponder at some point in their lives: if functions were superheroes, which would be on the Avengers?

Everyone is currently talking about the exponential function, so that’s clearly the one that likes to be in the spotlight. I’m going for Iron Man for that one.

The trigonometry functions are all about circles, and the Avenger who likes whirling things round in circles is Thor, so we’ll go for the sine function as Thor. Just $\cos $.

The Hulk blows up. Frequently. So we need a function that “blows up” on a frequent basis, and what better than the tangent function?

I’m not so sure about Black Widow and Hawkeye. I feel that these need to be “ordinary” functions, but with special skills. So I’m going for $x$ and $x^{2}$ for these two. Hawkeye is $x$: straight as an arrow. Black Widow is $x^{2}$: always the curveball.

Captain America is the most constant of all. You can always rely on Cap, so my function for him is the constant $1$.

(Nick Fury is clearly the zero function as he gives nothing away. And I’m going for $\tanh $ for Spiderman as he’s always off on a tangent and frequently hyper(bolic). Depending on your list of who is actually in the Avengers, this could go on for quite some time so I’ll get to the point now.)

What about Captain Marvel?

According to some, she is the most powerful Avenger. But on first look she doesn’t seem as powerful as, say, the Hulk. So it will have to be a function that doesn’t seem powerful when you first meet it, but once you see it in action you’ll have no doubt.

Without further ado, therefore, please allow me to introduce you to the Captain Marvel of functions: the absolute value function.

It may not look like anything particular on first encounter, but I promise you that it’s the most powerful function in the known universe.

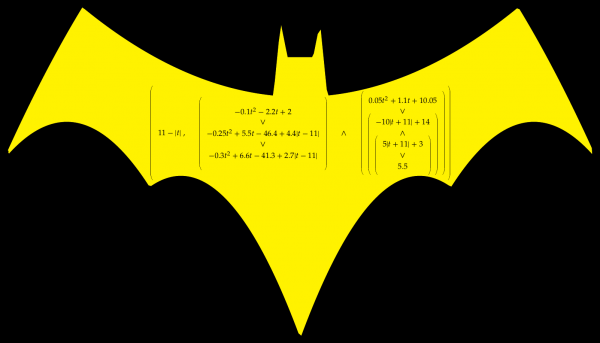
To explain why, I want to jump comic books and talk about Batman. Well, not Batman himself, but the Batman Curve. A few years ago some bright spark figured out a formula that when put into a graphing program would draw out one of the many Batman logos. Partly inspired by that, I designed an activity for my students which would get them to draw a different Batman logo by plotting quadratic curves (plus a few lines). You can read about that on my website.

As well as using simpler curves and a different logo, a big difference between my version and the original Batman Curve was that I presented mine as a list of distinct curves to draw. This meant that my version did not strictly speaking draw the Batman logo but rather defined a region comprising the logo.

A little while later, I thought about how one might fix that: put the curves used in my version into a single function. I view the way that the original Batman Curve does this as a bit of a kludge – it relies on how graphical software packages work rather than using something mathematical. So I looked around for another way to do it.

Enter the absolute value function, the most powerful function in existence. Powerful enough to weld curves together and warp them round its little finger.

You can read more about it on my website. But for those who don’t like clicking through, here’s the logo with the formula emblazoned on it.

Pat Ashforth and Steve Plummer – Tilting at Windmills

Pat Ashforth and Steve Plummer explore maths through knitting and crochet at woollythoughts.com.

Before you scroll down, I want to ask you a question – Is this a pattern?

You may think this is a totally pointless question. Try showing it to other people and see if their answer is the same as yours. You might be surprised.

I can guarantee it will provoke disagreements. There will always be some who land firmly on one side of the fence and can’t understand why there should be anyone on the other side. Discussions can get quite animated.

Tilting at Windmills was made, many years ago, entirely from squares that are navy on one side and some shade of pink/purple on the other. They had to be in the correct orientation but the choice of squares was mostly random. However, in a few areas, the colours were carefully chosen to give a hint of a repeated pattern. This had to be enough for the brain to think it was looking for a pattern but quickly be able to dispel the idea. It was deliberately confusing.

If the photo is recoloured I’m sure everyone would agree that it is a pattern. Before you scroll down look at the photo below, or the one at the top, and think about what you can see.

Did you see windmills (pinwheels)? Many people do. If you didn’t see them before, can you see them now? Are they light or dark? Which way are they turning?

You might have seen butterflies, bow ties, ‘diamonds’, lozenges, small squares, large squares. or many other different things. The more you look the more shapes you will see.

The first time we saw groups arguing it came as a bit of a shock. It became apparent that those who declared that it was a pattern were not taking notice of the colours at all. The shapes made a pattern and that was all that mattered. On the other side were those who insisted that if the colours were wrong it couldn’t possibly be a pattern. It certainly justified our arguments for not using colours in our Woolly Thoughts book, way back in 1994, though we had not been prepared for the extreme reaction whenever a group of people look at the hanging.

Why does it matter?

This has implications for normal classroom teaching. Almost every teacher provides pupils with coloured shapes for particular tasks but we rarely make it clear whether the colours are strictly relevant to the task. Perhaps those pupils who struggle are not seeing the task as we intended it to be.

Before you scroll down – can you see any tunnels?

We haven’t put this in front of a group for a long time but we recently had a visitor who came to our home so we asked her the usual questions.

I have been looking at it for over 20 years and I saw something I had never seen before. It might have been the effect of the light at that moment but I suddenly saw three tunnels. The really strange thing is that their outlines do not follow the lines in the divisions of the squares.

It troubled Steve that the inside/outside parts of the tunnels were ‘wrong’. He couldn’t accept them as tunnels but to me they very definitely were. I can see another tunnel above these and one below but they are not as well-defined. There is always something new to be discovered.

Can you ever be sure that other people see what you are seeing?

Just in case you were struggling to see windmills going in opposite directions, this photo might make them more obvious.

So, which bit of maths made you say “Aha!” the loudest? Vote:

 Loading ...

The poll closes at 9am BST on Monday the 13th, when the next match starts.

If you’ve been inspired to share your own bit of maths, look at the announcement post for how to send it in. The Big Lockdown Math-Off will keep running until we run out of pitches or we’re allowed outside again, whichever comes first.