Welcome to the 13th match in this year’s Big Math-Off. Take a look at the two interesting bits of maths below, and vote for your favourite.
You can still submit pitches, and anyone can enter: instructions are in the announcement post.
Here are today’s two pitches.
Brad Ashley – Counting on your hands
Brad is a final year maths undergraduate at Sheffield Hallam University. He tweets at @pogonomaths.
Counting on your fingers! One of the first mathematically abstract things we learn. Want to count up to 10 things? See how many fingers that is equal to, and you know how many things you have. Unfortunately, as we get older, we often find ourselves needing to count more than 10 things, so this old method is no good. Of course we could use our toes, but that’s just a bit impractical, or we could technology in some way, but where’s the fun in that? Here, I’m going to show you a few fun new ways to count on your fingers and how they relate to different base systems.
By The Dozen
On most hands, there are four fingers, excluding the thumb. Each of these fingers are divided into three sections attached by joints. So, in total, on your one hand that’s twelve sections. Using your thumb has a counter, we can count to 12, which is already more than we could count with the previous 1-10 system. Bring in your other hand, and that’s 24. But there’s more we can do with this. For every 12 we count on our left hands, we can move our right hand counter (our thumb) up by one, then start again with our left hand. So we count to 12, twelve times. That’s 144. These numbers are getting big quickly.
Unintentionally, we’re finding ourselves in the world of ‘number bases’. What we’re essentially doing here is counting in base-12 (also called the dozenal or duodecimal system), where each ‘digit’ (finger segment) on our left hand is some multiple of $12^0$, and each digit on our right hand is some multiple of $12^1$. Now, base twelve has two extra digits than base ten, so let us denote them $A$ and $B$, which are equivalent to 10 and 11 respectively in base-10. So, we count $1,2,3,4,5,6,7,8,9,A,B,10,11,12…$ in dozenal. Where each new column in base-10 represents ascending powers of 10, in doezenal, each new column represent powers of 12. Take 324 in base-10. This would be 3 ‘hundreds’ ($3\times 10^2$), 2 ‘tens’ ($2\times 10^1$), and 4 ‘ones’ ($4\times10^0$). Instead, in base-12, this number would be written as 230, given by $2\times 12^2 + 3\times 12^1 + 0 \times 12^0$.
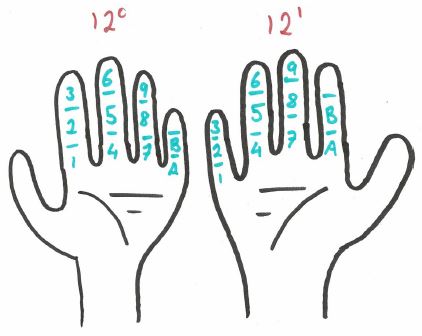
So, each digit would look like this on our hands. Note that I am most certainly not an artist, so please excuse the questionable illustrations. This allows us to retrieve the count from our hands. Take the following.
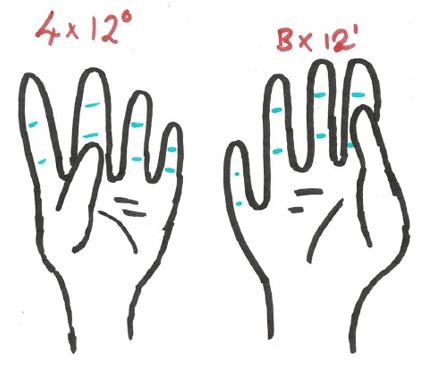
The left hand has the 2nd finger from left with the bottom segment marked, and the right hand has the far right finger with the middle segment marked. This leads to the following calculation.
\begin{align}
4 \times 12^0 + B \times 12^1 & = 4 \times 1 + 11 \times 12 \\
& = 135.
\end{align}
There, we have counted to 135, 13.5 times our previous base-10 limit! This way of counting on your fingers supports an argument made by many who believe we should completely replace our base-10 dependency with base-12. It’s a completely valid belief, and would even make fractions easier to understand. Where $\frac{1}{3} = 0.3333…$ and $\frac{1}{4} = 0.25$ in base-10, we have $\frac{1}{3}=0.4$ and $\frac{1}{4} = 0.3$ in base-12. This is due to 12 having more factors than 10 and are much nicer to work with.
Section 10
We can count much higher, however. Much like before, we’re playing with base systems. There exists a way to count up to 31 on one hand, and up to 1023 on two hands, using the magnificent power of base-2, commonly known as binary. Let each finger represent a digit in a binary string (we’re including thumbs this time). We can hold each finger in one of two positions; a finger down represents a 0 in our binary string, and a finger up represents a 1. We can then start from the thumb on the right hand, moving left through the fingers, counting in binary.
The issue here, however, is that most of us don’t count things using base-2 in our everyday lives, so we need some method to retrieve a base-10 count. Whereas with the base-12 counting system, each hand represented a power of 12, here, each finger represents a power of 2.
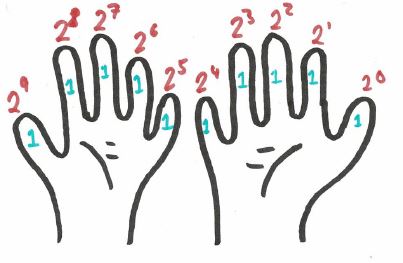
We can then look at how many of each power of 2 we have, add them up,
and get our total. So, if we include both hands, the binary string 1111111111 is the new highest we can count. Converted to base-10, this gives
\begin{equation}
\begin{split}
1 \times 2^0 + 1 \times 2^1 + 1 \times 2^2 + 1 \times 2^3 + 1 \times 2^4 + 1 \times 2^5 + 1 \times 2^6 + 1 \times 2^7 + &\\
1 \times 2^8 + 1 \times 2^9 \\
&= 1+2+4+8+16+32+64+128+256+512 &\\ &= 1023,
\end{split}
\end{equation}
an impressively high number. So, using this, we can count up in binary, and retrieve the base-10 total. Take the following hands (and yes, I realise how concerning that phrase would sound out of context).
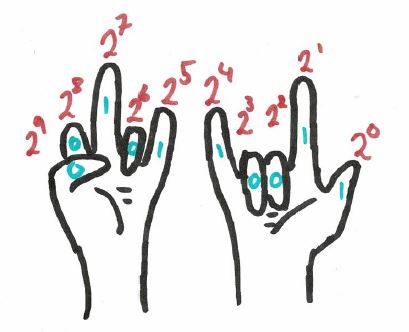
The devil horns are entirely unintentional, I promise. The binary string can be read straight from the fingers giving $0010110011$. We can then change the base by the following calculation.
\begin{equation}
\begin{split}
1 \times 2^0 + 1 \times 2^1 + 0 \times 2^2 + 0 \times 2^3 + 1 \times 2^4 + 1 \times 2^5 + 0 \times 2^6 + 1 \times 2^7 + &\\
0 \times 2^8 + 0 \times 2^9 \ = 1+2+16+32+128 &\\ &= 179.
\end{split}
\end{equation}
So, with this technique, we can count to much higher numbers than ever before! Theoretically, we could add another position fingers could be in, up, down, and middle. This would give us a base-3 system, and on two hands would allow us to count to 29524. We could keep adding positions to hold our fingers in, however it would eventually be difficult to tell the difference. This might not be the most practical solution to a problem no-one has, but it’s interesting at least. You can even choreograph a hand dance to help us remember, which is exactly what “recreational mathemusician\” and Youtube personality Vihart did!. So, next time you have the need to count something, but 10 fingers just isn’t enough, you’ll know exactly what to do!
Christian Lawson-Perfect – Interesting Esoterica
Christian blogs at The Aperiodical, and collects his other doings at somethingorotherwhatever.com. He toots at @christianp@mathstodon.xyz.

At a moment’s notice I can give you citations for twenty different papers linking maths and food. ‘Factoring in the Chicken McNugget monoid’ is my favourite. You might not be expecting it, or even want it, but if we’re eating chicken nuggets together that’s what’s going to happen.
Or if it’s not food but animals that you’re interested in, I have 32 references including “Hunting Rabbits on the Hypercube”, “The accuracy of Buffon’s needle: a rule of thumb used by ants to estimate area”, or possibly my favourite paper ever, “Robust Soldier Crab Ball Gate”.
The point is, I seem to be making it my life’s work to know a bit of maths to do with any topic that might come up in conversation, plus a load of other stuff that will never come up unless I try really hard.
Back when I was trying to be a proper mathematician, I started using citation management software to keep track of references for my purported PhD thesis. After a while, I realised that my collection had considerably more references to unusual things that had caught my eye than to anything that would help me understand the Grzegorczyk hierarchy.
In time, I gave up on being a proper mathematician, but I kept gathering these weird references. A few themes started to emerge. Among the first was “Attention-grabbing titles” – quite often, I’d save a paper not for its contents, but for the quality of its title alone. It was years before it even occurred to me to look inside “The effective content of Reverse Nonstandard Mathematics and the nonstandard content of effective Reverse Mathematics”, but that chiasmus makes me grin every time I see it.
What I really enjoy about having this growing collection of what I call ‘Interesting Esoterica‘ is being able to quickly remind myself of a puzzle or a weird maths fact I half remember. A few years ago I exported all my data from Mendeley and set up a little website to organise and present my collection. It’s rare that I meet another mathematician and don’t dig into it at least once. Most of the time, it’s to get a link to ‘Orange peels and Fresnel integrals’. I just love that paper.
There’s an element of curation now to what I put in the collection. I’ve got some named sub-collections, on particular areas of maths such as ‘Fibbonacinalia’ or ‘Unusual arithmetic’, or for particular purposes, such as ‘Lists and catalogues’ or ‘Games to play with friends’.
While trying to come up with ideas for Math-Off pitches, I always start by going to my Interesting Esoterica collection. I finally realised that, while I can tell you about fun maths facts like ‘every positive integer is a sum of three palindromes’, or brilliant puzzles like the princess in a castle problem, what I’m really passionate about is the unusual connections that you can find in the collection as a whole.
I can start by showing you something cool but reasonable, like the picture-hanging puzzle. Then, since the solution to that puzzle involves group theory I might remember about Mad Abel, the group-theoretical card game. Another card game is Poker, and I’ve always wanted to try out the zero-knowledge Poker protocol. If you don’t know what a zero-knowledge protocol is, please read the brilliant ‘How to explain zero-knowledge protocols to your children’ by the compellingly named duo of JJ and M Quisquater. To make that concrete, you could try out the zero-knowledge protocol for showing you can solve a Sudoku. Talking of Sudoku, there’s a fabulous paper called ‘The paramagnetic and glass transitions in Sudoku’, which I hope you’ll want to go and read right now. I haven’t mentioned the “Basically physics” collection yet, which is where I put things that might not really be maths but I can’t bear to leave out. For example, you can take your pick from “Can one hear the shape of a drum?” (answer: no) or “How to hear the shape of a billiard table” (invitingly positive). From there I hope you make the mistake of clicking through to the “Easily explained” collection, which is where I put things that I reckon I could explain at least the gist of to someone else without having to re-read the paper. The first entry here is the aforementioned Quisquater opus on zero-knowledge protocols, and the most recent is titled “Projectivizing Set”, which basically explains itself. In between, there’s the photoelectric number sieve (a series of bike chains which solved number theory problems faster than anyone alive), the twin towers of Hanoi puzzle (towers of Hanoi, but you’ve got two of it, and they start in different positions, and whatever you do on one you have to do on the other) and Renyi’s parking problem (if cars park at random on a street, what’s the expected proportion of space used? Answer: about 0.747)
I always end up looking up Renyi’s parking constant in Shamos’ catalog of the real numbers, and rediscover that it’s not included. Shamos’ catalog is like the hipster OEIS: it’s just a massive list of decimal numbers, along with some opaque formula or reference to explain what they mean, and I’ve never met another person who’s used it. I hope one day to achieve the beautiful singularity of purpose that Shamos exhibits. Until then, I’m going to keep collecting interesting esoterica.
I’m Christian Lawson-Perfect, and I have a maths problem.
So, which bit of maths made you say “Aha!” the loudest? Vote:
Match 13: Brad Ashley vs Christian Lawson-Perfect
- Brad with finger counting
- (54%, 28 Votes)
- Christian with interesting esoterica
- (46%, 24 Votes)
Total Voters: 52
This poll is closed.
The poll closes at 9am BST on Thursday the 7th, when the next match starts.
If you’ve been inspired to share your own bit of maths, look at the announcement post for how to send it in. The Big Lock-Down Math-Off will keep running until we run out of pitches or we’re allowed outside again, whichever comes first.
One Response to “The Big Lock-Down Math-Off, Match 13”