Welcome to the 16th match in this year’s Big Math-Off. Take a look at the two interesting bits of maths below, and vote for your favourite.

You can still submit pitches, and anyone can enter: instructions are in the announcement post.

Here are today’s two pitches.

Christian Lawson-Perfect – Putting coins in order

Christian blogs at The Aperiodical, and collects his other doings at somethingorotherwhatever.com. He toots at @christianp@mathstodon.xyz.

This is a ramshackle video about a puzzle I like. It’s not very complicated, and makes a good brainteaser when you’re in a pub and you’ve already done the height-v-circumference thing with a pint glass. (Remember pubs? Cor!)

Here’s the gist: get one of each denomination of coin, shuffle them up, and lay them in a line. By swapping a pair of coins at a time, can you put them in ascending order? Without touching any coins, can you say how many moves it’ll take?

I fluffed up the explanation at the end of the video a bit. The key is to notice that you can separate the coins into independent cycles, and then each cycle of $n$ coins takes $n-1$ moves to put in the right place.

Peter Rowlett – Art Gallery Problems

Peter Rowlett is a maths lecturer at Sheffield Hallam University. You can find him on Twitter at @peterrowlett.

Art Gallery Problems are concerned with finding the minimum number of guards necessary for a polygon, the ‘art gallery’, to be ‘guarded’. For an art gallery to be guarded, we we require that every point in its interior can be connected by a straight line (line of sight) to at least one guard. Guards, then, are taken to be able to see a full 360° around themselves over any distance (just like humans can, right?).

Convex polygons

A convex polygon is one for which every point can be connected to every other point by a straight line which does not leave the polygon. For example, imagine holding a piece of string tight between two hands; everywhere you move your hands within a drawing of a polygon, the string should still be inside the polygon.

Below are examples of convex and non-convex polygons. Can you see why one is convex and the other is not?

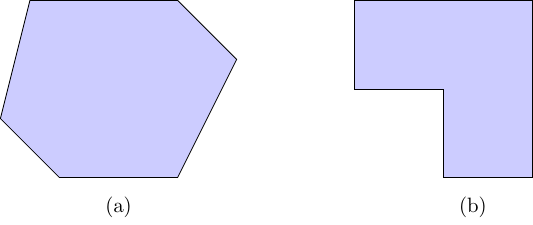
For a convex polygon, a single guard is sufficient and can be placed anywhere. For non-convex polygons, multiple guards may be required.

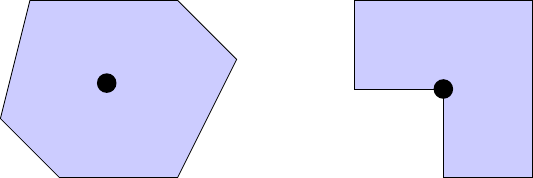
The art galleries below are each guarded by a single guard, represented by a black dot. Hopefully you agree the guard in the convex polygon can see all points in the polygon, and still could even if moved around the gallery. In the non-convex polygon, do you agree the guard can still see every point in the gallery? Could you move the black dot in the non-convex gallery to an interior point such that it isn’t in line of sight of the whole interior?

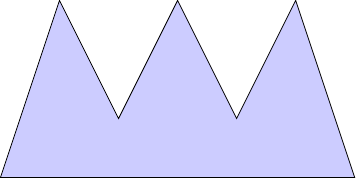
Naturally, galleries can be imagined which require many more guards.

The story goes that in 1973, Vasek Chvátal asked Victor Klee for an interesting geometric problem to work on. Klee responded with the problem of determining the minimum number of guards sufficient to cover the interior of an \(n\)-wall art gallery room.

In 1975, Chvátal published a theorem proving that \( \lfloor \frac{n}{3} \rfloor \) guards are always sufficient and sometimes necessary to guard an \(n\)-sided simple polygon. (The floor function, e.g. \( \lfloor x \rfloor \), is said “floor of \(x\)” and resolves to the biggest integer \(\le x \).)

The proof is quite complicated, but in 1978, Steve Fish published an alternative, simpler proof of Chvátal’s Art Gallery Theorem.

Take an art gallery that is a polygon. The first step is to ‘triangulate’ the polygon. This means adding interior diagonals between vertices of the polygon to form triangles everywhere. (Questions to arm-wave through: can every polygon be triangulated? Is the resulting triangulation unique?)

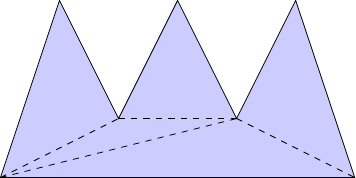
This triangulated polygon can then be three-coloured. This means its vertices can be coloured using not more than three colours such that no adjacent pair of vertices are the same colour. (Can all triangulated polygons be three-coloured? Is such a three-colouring unique?)

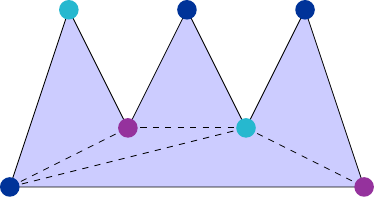
As at most three colours have been used, we can say that at least one colour has been used at most \( \frac{1}{3} \) of the time, i.e. for at most \( \lfloor \frac{n}{3} \rfloor\) vertices. Since each triangle in the triangulation is itself a convex polygon, placing a guard at any point in each allows the entire interior to be guarded. Placing guards at the points coloured with the colour used least often allows every point in the polygon to be in line of sight of a guard, using at most \( \lfloor \frac{n}{3} \rfloor\) guards.

For example, in the three-colouring above, there are two purple vertices, two light blue vertices and three dark blue vertices. A minimal arrangement of guards could be found by placing guards at either both the purple vertices or both the light blue vertices. Note that there are seven vertices, and \( 2 \le \lfloor \frac{7}{3} \rfloor \).

So, which bit of maths made you say “Aha!” the loudest? Vote:

 Loading ...

The poll closes at 9am BST on Wednesday the 13th, when the next match starts.

If you’ve been inspired to share your own bit of maths, look at the announcement post for how to send it in. The Big Lockdown Math-Off will keep running until we run out of pitches or we’re allowed outside again, whichever comes first.