Welcome to the 17th match in this year’s Big Math-Off. Take a look at the two interesting bits of maths below, and vote for your favourite.
You can still submit pitches, and anyone can enter: instructions are in the announcement post.
Here are today’s two pitches.
Pat Ashforth and Steve Plummer – Dragonometry
Pat Ashforth and Steve Plummer explore maths through knitting and crochet at woollythoughts.com.
What is the connection between these?

They both represent dragon curves!
Take a long strip of paper and fold it in half, then in half again. Open it up and crease it firmly on the folds, taking care not to bend them in the wrong direction. Make as many folds as your paper allows, always folding in the same direction. You get these after the third, fourth, fifth and sixth folds.
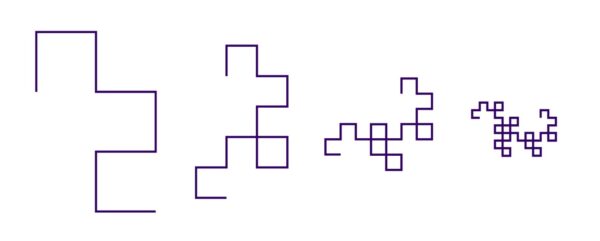
By now, with a bit of imagination, you can see why they are called dragon curves. They get more and more tightly packed as you make more folds. The corners of the paper meet but cannot cross. On the next drawing the corners have been rounded so you can see which parts are joined and which are merely touching.
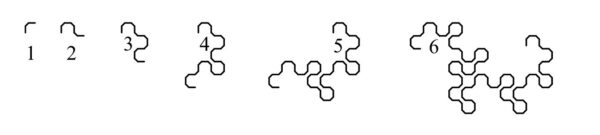
It soon becomes impossible to fold the paper any more but they can be drawn. A dragon with one fold (an order 1 dragon) has two sections. Order 2 has four sections but only three folds. Order 3 has eight sections and seven folds. The number of sections is a power of 2; the number of folds is the power of 2 minus 1.
Notation can be used to describe which way the folds go on the opened out strip. They can be thought of as In folds and Out folds (I and O). The I and O could also stand for one and zero, if you find it easier to think in these terms. It doesn’t really matter which folds are described as In and which is Out as long as a consistent system is used.
The sequence of folds for the Order 3 Dragon (the first one shown above) is O O I O O I I . Starting from the top it goes in the same direction for the first two folds, then it goes the other way once, then the first way twice and, finally, the second way twice.

Before long it becomes impossible to fold the paper so a system is needed.
How would you do it?
There are two ways of generating successive sequences.
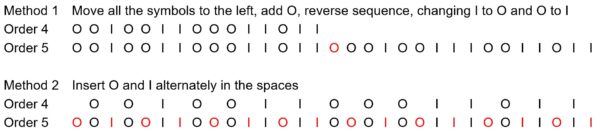
O folds are orange lines, I folds are ivory lines.

O folds are orange lines, I folds are ivory lines.
This doesn’t explain anything about how dragons fit together. Perhaps that’s a story for another day.

We invented the term Dragonometry after spending about 18 months playing with dragon curves in different ways.
Will Barrass Hemmens – The Simplex Family and Empty Space
Will is a maths teacher in Harrogate. He very rarely tweets at @wsbarhem.
The Simplex Family is the generalisation of $n$ dimensional objects based around an equilateral triangle. When exploring the various components of this family it throws out a wonderful and unexpected question.
We will grow the family starting from a single vertex, to an edge, a triangle and beyond.
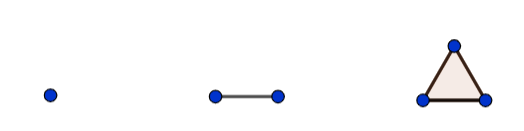
The early table may not look that interesting, but we can establish some patterns.
| Dimension | Vertices (0d) | Edges (1d) | Faces (2d) | Tetrahedrons (3d) |
| 0 | 1 | 0 | 0 | 0 |
| 1 | 2 | 1 | 0 | 0 |
| 2 | 3 | 3 | 1 | 0 |
| 3 | 4 | 6 | 4 | 1 |
The number of vertices only increases by 1 each time, the number of edges connected to a vertex is the same as the dimension of the object and the number of faces meeting an edge is one less than the dimension of the object.
These observations allow us to take the table on to further dimensions.
| Dimension | Vertices (0d) | Edges (1d) | Faces (2d) | Tetrahedrons (3d) | 4-simplexes (4d) | 5-simplexes (5d) |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 1 | 2 | 1 | 0 | 0 | 0 | 0 |
| 2 | 3 | 3 | 1 | 0 | 0 | 0 |
| 3 | 4 | 6 | 4 | 1 | 0 | 0 |
| 4 | 5 | 10 | 10 | 5 | 1 | 0 |
| 5 | 6 | 15 | 20 | 15 | 6 | 1 |
You may have started to notice that the table is starting to look a little ‘binomially’, but with one important omission.
Where is the leading 1 and what does it represent?
Perhaps the 1 describes the infinite empty space that surrounds the objects in our family. If that is the case, what is its dimension?
So, which bit of maths made you say “Aha!” the loudest? Vote:
Match 17: Pat Ashforth and Steve Plummer vs Will Barrass Hemmens
- Pat and Steve with the dragon curve
- (80%, 32 Votes)
- Will with the simplex
- (20%, 8 Votes)
Total Voters: 40
This poll is closed.
The poll closes at 9am BST on Friday the 15th, when the next match starts.
If you’ve been inspired to share your own bit of maths, look at the announcement post for how to send it in. The Big Lockdown Math-Off will keep running until we run out of pitches or we’re allowed outside again, whichever comes first.