Welcome to the nineteenth match in this year’s Big Math-Off. Take a look at the two interesting bits of maths below, and vote for your favourite.

You can still submit pitches, and anyone can enter: instructions are in the announcement post.

Here are today’s two pitches.

Alex Corner – The Sofa Moving Problem

Alex Corner is a lecturer at Sheffield Hallam University interested in category theory and maths education. You can find him as Fabstract Nonsense on Twitter at @alexcorner.

“Odd,” agreed Reg. “I’ve certainly never come across any irreversible mathematics involving sofas. Could be a new field. Have you spoken to any spatial geometricians?”

Douglas Adams, Dirk Gently’s Holistic Detective Agency

If you’ve ever tried to move a sofa into a home, then you might know that it’s not always easy to do. It might depend on the walls, the doors, or the shape and size of the sofa. Various people have pondered the moving sofa problem since the 1960s, although there is some reference to it being talked about before then. The simplified setup for the problem is simply to describe the shape of a sofa with the largest area possible which can be moved round the corner of a right-angled corridor with, say, width $1$.

I’ve never really looked too much into this problem, despite my family trade being upholstery! This year I’ve set it as a final year project, which means I shold hopefully learn a lot more about it. I’ll accompany this with some very crude animations I made in MATLAB.

What we’ll do here is just look at a few of the possible solutions, then I’ll leave it up to you if you want to get into the details. Now the first solution is really simple. It’s just a square.

This is fine, though you wonder now if you have ever seen a square sofa. Isn’t that just a chair? Anyway, this has area $1$, so we’ve at least got a starting point. Another option is to chop a disk of radius $1$ in half. Of course, this will have area $\frac{\pi}{2} \approx 1.5708$.

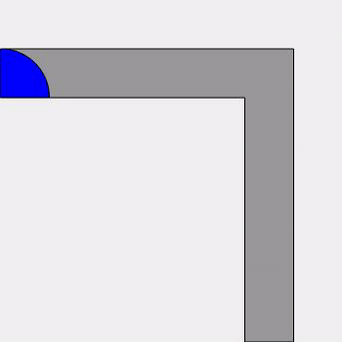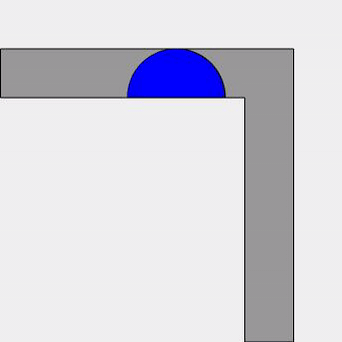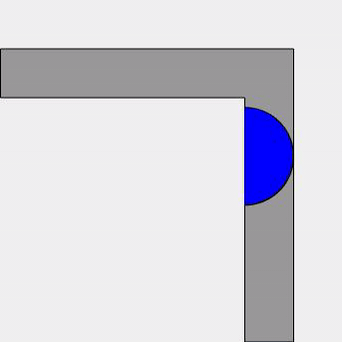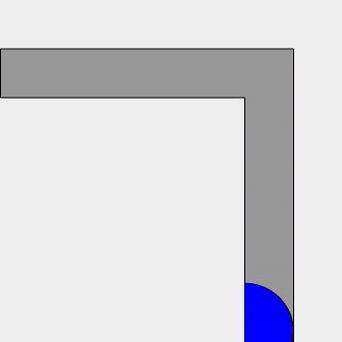
That’s slightly more sofa-shaped at least – I can imagine two people sat on it. But what about improving that area? Are there any sofas which have a larger area which can still move around the corner? Well, John Hammersley gave a decidely futuristic looking design, the area of which is a much improved lower bound to the problem and is given by the very pleasing value of \frac{\pi}{2} + \frac{2}{\pi} \approx 2.2074. Simply described, we have a quarter-disk of radius $1$ at each end, connected by a rectangle of width $1$ and length $\frac{4}{\pi}$. At the bottom of that rectangle is carved out a half-disk of radius $\frac{2}{\pi}$. It might be easier to look at the picture.

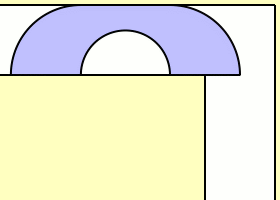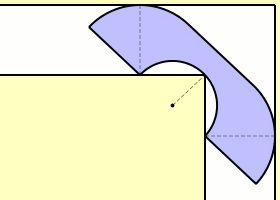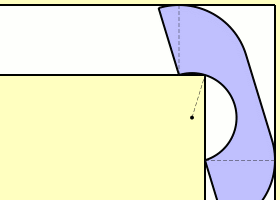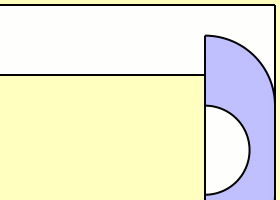
I managed to animate the Hammersley sofa up until the corner but then decided to just go look for a pre-made version (you don’t want to see the mess I made in MATLAB).

Now there is a futher sofa which I will mention, which is the Gerver sofa, found in 1992. The area isn’t improved on much (approx. $2.2195$) and it is much more difficult to describe; the curves result as solutions of a system of differential equations. It might be the optimal solution but we just don’t know!

Vicky Neale – The Big Lock-Down Math-Off 2020 Even More Unofficial Offline Hedgehog Sticker Book

Vicky Neale is the Whitehead Lecturer at the Mathematical Institute and Balliol College, University of Oxford, which means her job is to be enthusiastic about mathematics with undergraduates, school students, and anyone else she can find. She is the author of Closing the Gap: the quest to understand prime numbers. She’s @VickyMaths1729 on Twitter.

For many fans of the Big Math-Off, one highlight of the 2019 event was the associated sticker book, so imagine the delight when we discovered that the Big Lockdown Math-Off has the associated Big Lock-Down Math-Off 2020 Unofficial Online Sticker Book, created by Matthew Scroggs. We have exciting stimulating mathematical content in the Big Math-Off pitches, and that is celebrated in the sticker book.

I have been wondering: what exciting stimulating mathematical content can we find in the sticker book? I started thinking about this during the 2019 Math-Off, and have been pondering some more. I have a small thought to share with you, relating to a serious application of mathematics and computer science to the non-sticker-book world, but mostly I hope that this post will stimulate further discussion.

The Big Lock-Down Math-Off 2020 Unofficial Online Sticker Book already (at the time of writing) has 306 stickers available to collect, many users, and extra levels of complexity with different locations where people can buy stickers, and even options to personalise your avatar. So for the purposes of simplicity in this post I’ve asked my baby hedgehogs to share their simpler Big Lock-Down Math-Off 2020 Even More Unofficial Offline Hedgehog Sticker Book with you.

How does the Big Lock-Down Math-Off 2020 Even More Unofficial Offline Hedgehog Sticker Book work, you ask? It’s a lot like the Big Lock-Down Math-Off 2020 Unofficial Online Sticker Book, but, well, with more hedgehogs. But if you know about the online one already, then you know the idea.

Each of my three baby hedgehogs has their own sticker book. Each morning, they get their imaginary money, which they can spend in the sticker shop. In total, there are 10 stickers to collect.

If a baby hedgehog gets a sticker that they haven’t already got, then they stick into their sticker book. If it’s a duplicate, then it is added to their collection for swapping.

Each baby hedgehog can choose to be friends with any of the others, and since my lot are a nice group, they are all friends. This means that any one of them can propose a swap with another baby hedgehog. They can see which swaps their friend has, and they can see which of their swaps their friend wants.

Here are a couple of questions I’ve been wondering about. Might it be that at some stage the hedgehogs have collectively bought all the stickers that the baby hedgehogs need to complete their sticker books, if only they could swap them to the right hedgehogs? At the start, this was not the case, but after a few days of buying packs of stickers, there are plenty of stickers in play. And might it be that an altruistic hedgehog could facilitate a swap between two others who aren’t friends?

In the less hedgehoggy sticker book, there are 93 named participants and another 375 anonymous users (at the time of writing). Some of those are not very active, some are collecting and swapping daily. I apparently have 66 friends. I don’t know how typical that is — are most people friends with most people? I’m not sure.

I can go through all 66 of my friends, one at a time, to see which swaps I have that they might want, and to see whether they have any spare stickers that I’m still looking to collect. Of course I mostly focus on swaps where both parties gain a sticker they wanted, but also I wonder whether I can be a useful broker, facilitating swaps between people who might not already be friends, or perhaps initiating a chain of swaps that collectively leads to progress.

Example 1

Here’s one example. Imagine that two of my baby hedgehogs have not yet made friends. We can show this via a graph, where a (h)edge indicates friendship between hogs.

Summary:

• Hog A needs sticker 7, and has swaps 1, 3, 5, 6, 9
• Hog B needs sticker 2, and has swaps 3, 4, 5, 6, 8, 9, 10
• Hog C needs sticker 4, and has swaps 1, 2, 5, 6

In this situation, hog A doesn’t gain by swapping with hog B or hog C: nobody has the one sticker that A needs. And B and C can’t swap because they’re not friends. But A can facilitate a chain of swaps that has the same net effect as B and C directly swapping stickers 2 and 4. For example:

• A,B swap stickers 1 and 4 (now A has swaps 3, 4, 5, 6, 9 and B has swaps 1, 3, 5, 6, 8, 9, 10)
• then A,C swap stickers 3 and 2 (now A has swaps 2, 4, 5, 6, 9 and C has swaps 1, 3, 5, 6)
• then A,B swap stickers 2 and 1 (now A has swaps 1, 4, 5, 6, 9 and B has swaps 3, 5, 6, 8, 9, 10 — and 2 is now in B’s sticker book)
• then A,C swap stickers 4 and 3 (now A has swaps 1, 3, 5, 6, 9 and C has swaps 1, 5, 6 — and 4 is now in C’s sticker book)
• This leaves A with the same stickers as before, but B and C have swapped 2 and 4 (and stuck them in their sticker books)

Example 2

In this example, the hedgehogs are all friends with each other.

Summary:

• Hog A needs sticker 7, and has swaps 2
• Hog B needs sticker 2, and has swaps 4
• Hog C needs sticker 4, and has swaps 7

There is no immediate incentive for anyone to swap, because there is no swap that benefits both parties. But there is a chain of swaps that leads to all the hedgehogs filling their sticker books:
A and B swap 2 and 4 (so 2 goes in B’s sticker book, and A has swap 4)
then A and C swap 4 and 7 (so 4 goes in C’s sticker book, and 7 goes in A’s sticker book).

Conclusion

With both these examples, you and I have the benefit of knowing everything: we can see all the information about which hedgehogs have which stickers and swaps. In reality, altruistic hog A can’t see enough information to be confident that their plan will work. In both examples, hog A knows that hogs B and C are each missing one sticker, but can’t infer from the swaps which sticker that is, and so might not have a suitable strategy.

So how can A facilitate these kinds of swaps? I’m not really sure. Even if A had more data, if hog A had lots of friends then it would be rather impractical to try to trawl through to spot these sorts of chains of swaps.

And this brings me to a serious point: related sorts of mathematical thinking are helping patients on the waiting list for a kidney transplant. In the UK, the NHS runs a Living Kidney Sharing Scheme. A patient needing a new kidney might have a friend or relative willing to donate a healthy kidney. If the patient and their donor are compatible, then this can go ahead. But sometimes the donor’s kidney is not suitable for the patient. If there are two such pairs, then it might be that they can swap: donor A gives their kidney to patient B, and donor B gives their kidney to patient A. More complicated chains are possible too, including those prompted by an altruistic donor offering a kidney without having a particular patient they wish to help. To go through the records to find suitable exchanges is potentially a computationally intensive task, and researchers have found more efficient ways to carry out this task. The OR Society has published a case study with some information about this project.

Thank you to the baby hedgehogs for allowing me to share their sticker books with you. Apologies that our local sticker supplier can only print in black and white.

And finally…if this post gets published, then hopefully that means that one day there will be a sticker in the Big Lock-Down Math-Off 2020 Unofficial Online Sticker Book about the Big Lock-Down Math-Off 2020 Even More Unofficial Offline Hedgehog Sticker Book, which will make my baby hedgehogs’ day.

So, which bit of maths made you say “Aha!” the loudest? Vote:

 Loading ...

The poll closes at 9am BST on Tuesday the 19th, when the next match starts.

If you’ve been inspired to share your own bit of maths, look at the announcement post for how to send it in. The Big Lockdown Math-Off will keep running until we run out of pitches or we’re allowed outside again, whichever comes first.