Welcome to the twentieth match in this year’s Big Math-Off. Take a look at the two interesting bits of maths below, and vote for your favourite.
You can still submit pitches, and anyone can enter: instructions are in the announcement post.
Here are today’s two pitches.
Nikki Rohlfing – Star Polygons
Nikki Rohlfing is a heavy metal roadie turned maths teacher. On twitter he is @heavymetalmaths.
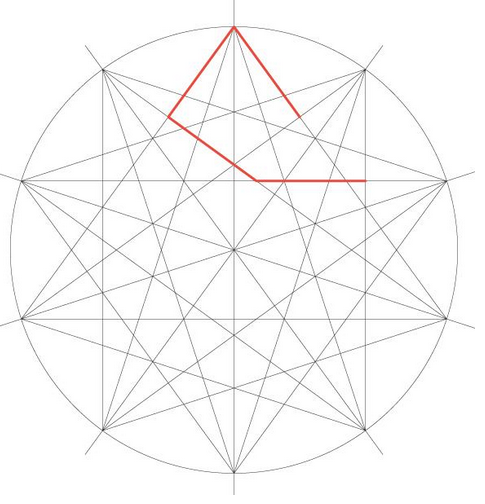
When I was a kid, one of the things my mum taught me was how to draw the star below, including the rhyme:

I enjoyed drawing this star, although the accuracy could be tricky, and depending how you drew the lines, the middle of the star could be an octagon, but potentially also a square, or most likely, a mash up of both…. Nevertheless, it’s something I can still produce now without thinking (which is handy when drawing a 2D version of a tesseract, for example).
Fast forward 20 years or so, and it turns out I’d been drawing an Octagram, which is a star polygon with Schläfli symbol $\{8/3\}$ (more on that later). So only now do I realise I’d been tricked into doing maths from a young age, which includes the Cuisenaire rods I always thought were just toys….
These Octagrams pop up in all sorts of places: Eric Carle’s children book “draw me a star”, or the compass showing the cardinal directions of the 8 principal winds, or the “selburose” knitting pattern found on Norwegian gloves.
A perhaps more obvious appearance for these star polygons is in Islamic patterns. For those who haven’t tried, I find drawing Islamic patterns can be quite a meditative process, so perhaps helpful given the current situation! So by all means play along; let’s start with 10 points equally spaced apart around a circle. You can either construct this from scratch yourself (for example, quick search gives videos such as this by Arthur Geometry) or you can use a “here’s one I made earlier” file from this useful google drive from Eric Broug.

The next thing to do, is to consider the different ways we can connect these 10 points to one another. For example, we could join every point to its immediate neighbour, creating a decagon. What if we joined every point to one 2 steps away? Or 3? The shorthand for this, is the afore mentioned Schläfli symbol, so in this case $\{10/2\}$ is joining every second, and $\{10/3\}$ every third etc. and the first number in the brackets denote how many vertices the polygon has. By all means have a go before scrolling further!
I hope the star polygons have been both pleasant to create, look at, as well as muse about their mathematical features. For recreational purposes, here is how the mathematical knowledge may speed up the process of drawing an Islamic pattern:
Instructions: draw $\{10/3\}$ and $\{10/4\}$ on the same circle, then use a nice coloured pen to trace out the pattern.
Hopefully that activity created enough content on the page so that people could investigate a bit without seeing the spoilers below! So let’s look at the maths a little bit more: So considering $\{n/p\}$, how might things look for different $n$, or different $p$? Which combinations create star polygons which meet every point without having to take the pen off the paper, like the original $\{8/3\}$ mentioned? Although I have no proof, I suspect it’s when $n$ and $p$ are coprime. And I sometimes think it could be related to Matt Scroggs’s braiding.
Amongst the many mathematical patterns, one that I particularly enjoyed was working out the sum of the angles in the points of the stars. There is a pattern as we shift through different values for $n$ and $p$ (eg. check the first polygon in each row!). There are plenty more patterns to be found – please do tweet me any interesting ones that you find, I always like adding to my collection!
Here is a visual aide to help enjoy the pattern-hunt.

Perhaps you’ve already done it (there’s always one!), but what if we decide to draw $\{10/2\}$, $\{10/3\}$, $\{10/4\}$ etc. all on the same circle? What you get is called The Mystic Rose, which you can have a play with here if you fancy changing the n value.

There is so much maths to work through here, for example: trying to find an nth term for number of lines, number of regions, number of triangles, intersection of chords, how many different polygons, links to graph theory and the handshake problem etc.
Here are the first few to help you have a think:
Careful though, the formula for area seems to take a $2^n$ sort of approach, but that is wrong! Maths does have that about it, which is why perhaps proof can be so difficult at times. I’ll “leave it as an exercise for the reader” to work it all out, and instead, share another website where you can have fun creating pretty pictures!
Try the Star Polygon Generator.
Mark Cloud – Stuck In Another World: A Problem in a Non-Euclidean Space
Mark is a teacher of mathematics and a student of logics, classics and other ics. He tweets at @markdcloud1.
From time to time I like to visit other worlds. Recently, I have found myself perplexed by an occurrence in one of these other worldly spaces. I have thought about it, asked colleagues, searched the interwebs and world wide nets, consulted with those much better traveled than I and yet I still cannot quite reconcile how this works. So this is perhaps not so much a pitch of some interesting mathematics as it is a plea for assistance.
The world in which I seem to have become stuck is often called Taxicab Geometry or Manhattan Geometry. It is wonderful place to visit, especially for those who are at the early stages of their mathematical travels. It is a non-Euclidean space but one in which the non-Euclidean aspects are fairly easily understood and the computations fairly straight forward. Even so it is a world in which familiar objects quickly reveal themselves to be unfamiliar. If you have not traveled to this space, I would invite you to pause your reading of this and go spend some time there. It is a world that never fails to give the new visitor that particular, wonderful feeling of amazement that is unique to mathematical revelation and discovery.
The difference between Euclidean space and this Taxicab space is in the metric used to measure distance between two points. In Euclidean space, distance between \(A\) and \(B\) is defined as the length of the segment which would make the hypotenuse of a right triangle (red segment in Figure 1). In this space, the distance between \(A\) and \(B\) is the sum of the lengths of the legs of the right triangle. The analogy, and origin of the name of the space, is that if you are in a city with a grid of streets a cab must travel along the streets. Property owners get upset when you attempt to drive through the block. The smallest number of blocks the cab could travel would be the legs of the right triangle (blue segments in Figure 1)
Note that the green path has the same endpoints and length of the blue path. I point it out because perhaps it is important to my predicament.

By just changing the metric this world looks dramatically different than the familiar Euclidean world. One of the first differences a traveller encounters is the circle. (Warning: Spoilers are coming so if you are not familiar with this world go explore!) A circle with radius of 5 is shown in Figure 2. It has its center at \(S\) and \(T,A,M\) and \(H\) are all on the circle since they are 5 blocks away \(S\). Note that \(X\) is out side the circle. It is 7 blocks away from \(S\).
This assumes that in our city each block is divided by an infinite amount of alleys, lanes and bike paths that allow us a continuous curve

The first thing most students learn about circles is how to find the circumference. To do this we could add the lengths of the four arcs (\(TA, AM, MH\) and \(HT\)) that make up the circle. Each arc is 10 blocks so the circumference would be 40 blocks. Let’s compare this to what is often taught as a formula for circumference \(C = 2\pi r\) where \(r\) the length of the circle’s radius. Does this formula still apply in this new world? A quick glance leads us to believe it does not. The only thing, however, that we have changed is the metric for distance. The definition of \(\pi\) as the ratio of a circle’s circumference to its diameter stays the same. The formula for circumference is practically a definitional truth. What has changed is the value of \(\pi\). In this world \(\pi = 4\).
Not that standard textbooks address this at all
All of this is standard textbook stuff. Where my problem arises is in that next measurement students are taught — area. I have been told that area is found in the same way in this Taxicab Space as in Euclidean Space. If a cab drove north 3 blocks, west 2 blocks, south 3 blocks and east 2 more, the path would have enclosed an area of 6 blocks which is the classic length times width of a rectangle. I have been assured that the area of a circle is also calculated in the same way as it is in Euclidean space \(A = \pi r^2\).
In one of those wonderfully impish wonders of the English language the unit of blocks is used for both length and area (or at least that is how I have been taught).
And herein lies my confusion. According to the formula the blue circle of radius 5 in Figure 2 would have an area of 100 blocks. If we keep length times width as our formula for area of a rectangle the large square outlined by the red, dashed line in Figure 2 would enclose an area of 100 blocks. Now point \(X\) is in the square but not in the circle. The square encloses all the points enclosed by the circle and many others as well. Yet both figures have the same area. This confuses me.
Perhaps it is my understanding of area that is misguided. I think of area as a quantification of the amount of points enclosed by a figure. With that understanding of area, this scenario is very strange since the square encloses more points than the circle but both objects have the same area.
Perhaps my calculation of the circle’s circumference is wrong, after all in Euclidean space the distance between two points on a circle is cord length not arc length. If circumference is wrong then the value of \(\pi\) may not be 4.
Perhaps the object defined by the red, dashed line in Figure 2 is not a square. The object’s perimeter is the same as the circle’s circumference. The blue path that has endpoints at $M$ and $T$ has the same length as the red path with the same endpoints. Are these considered the same line, equivalent lines or are there multiple straight lines that connect the same points in this space? Furthermore what is a right angle in this space? Can a rectangle really exist in this space?
Perhaps I am mixing spaces. I am treating the circle as an object in Taxicab space but using a Cartesian coordinate system may not be legitimate. Could it be some type of Banach-Tarski scenario where points do not behave in the way I am used to. Or perhaps the formulas for area from Euclidean space do not work in this space and the whole thing must be rethought.
I don’t know but that is my problem. Maybe it is one of the possibilities I mentioned or maybe some other explanation. Any help explaining this (preferably in a way that I can understand) would be so appreciated. I enjoy travelling to these different worlds but I don’t seem to be able to leave this world until I understand what is going on. Thank you in advance for your help.
So, which bit of maths made you say “Aha!” the loudest? Vote:
Match 20: Nikki Rohlfing vs Mark Cloud
- Nikki with star polygons
- (58%, 22 Votes)
- Mark with Taxicab space
- (42%, 16 Votes)
Total Voters: 38
This poll is closed.
The poll closes at 9am BST on Thursday the 21st, when the next match starts.
If you’ve been inspired to share your own bit of maths, look at the announcement post for how to send it in. The Big Lockdown Math-Off will keep running until we run out of pitches or we’re allowed outside again, whichever comes first.




Regarding Mark Cloud’s pitch:
– first formal issue: “non-Euclidean” is usually reserved for specific class of things, rather than “anything different than something that is named after Euclid” (a bit like “irrational number” is a *real* number that is rational, not any number that is rational). Manhattan metric behaves very similar to Euclidean metric. Many games are based on Manhattan or Chebyshev metric and they do not feel weird, while a game based on a hyperbolic grid definitely feels non-Euclidean. (I have talked about this here)
– second issue: π is defined as the ratio of circumference to diameter in Euclidean geometry, or using another, equivalent definition (for example, half of the imaginary period of the exponent function, which is more difficult to explain to schoolchildren, but simple to define from basic principles). If you are using a ratio of circumference to diameter in some other metric, you should not call it π (otherwise it is confusing). (Especially that, in non-Euclidean geometries (i.e., hyperbolic or elliptic), this ratio depends on the diameter, and its limit is π as the radius tends to 0.)
– In the Euclidean plane, area is a measure such that a KxK square always has area $K^2$. I do not know whether any commonly accepted definition of area exists for the taxicab metric, but I think there is no reason why we should change anything, so the KxK should still have area $K^2$. (There is a standard definition of area in non-Euclidean geometries and other Riemannian manifolds — note that there are no squares with four right angles, so you need to try a bit harder to define the area there — but taxicab is not a Riemannian manifold.) This definition should be enough to prove that the area of the blue square is 50.
– So let’s denote the ratio of circumference to diameter by C and the ratio of area to radius squared by A. In Euclidean geometry we have C=A=π, but this does not mean that C should equal A in any other metric space. Here we have C=4, A=2, and there is nothing weird about it.