Welcome to the twenty-first, and possibly final, match in this year’s Big Math-Off. Take a look at the two interesting bits of maths below, and vote for your favourite.

You can still submit pitches, and anyone can enter: instructions are in the announcement post.

Here are today’s two pitches.

Peter Rowlett – Ox Blocks

Peter Rowlett is a maths lecturer at Sheffield Hallam University. You can find him on Twitter at @peterrowlett.

Ox Blocks is a game that promises on the box “Noughts and Crosses with a novel twist”.

The game comes with nine cubes, on which two faces are Cross, two are Noughts and two are blanks – actually, a hollow going right through the block. Gameplay involves rolling the cube. If it lands on Nought or Cross, you must play it on the board, regardless of whether it is your symbol or your opponent’s. If it lands on blank, you must remove a piece from the board.

How does this affect the game play? How do these blocks roll? How can you play (and you can) if you don’t have an Ox Blocks set at home?

I offer two options for you to answer these questions and more.

1. Read a blog post about ‘Ox Blocks probabilities‘;
2. Listen to an episode of the Mathematical Objects podcast, ‘Ox Blocks‘.

It’s a fun variant on Noughts and Crosses. Enjoy!

Fergus Powell – Have a Little Patience

Fergus is a Sci Comm student at the University of Manchester. He tweets at @FergusPowell.

When I was younger, I enjoyed playing Clock Patience with my Dad. For those who aren’t familiar with the game, you start by taking a standard deck of cards (with jokers removed) and dealing out 12 piles of 4 cards in a circle, with the 4 remaining cards in the centre.

You turn over the first central card and place it in the correct position around the “clock face” you have created – in this case, position 8. You then flip the top card in pile 8, place that card in its correct position, and so on. Jacks go in position 11 and Queens in position 12.

You continue placing and flipping cards until you turn over a King, which goes in the centre. You then start again with the next central card.

Play continues until either:

• You have revealed all 4 Kings, in which case you LOSE
• All outer piles 1-12 are completed without all Kings being turned over, in which case you WIN

In this example game, it came down to the final two cards. Unfortunately, the King was turned over and I lost.

It’s quite strange that I enjoy this game, to be honest. For a start, there’s absolutely no skill involved – it’s a completely mechanical game. Secondly, I never seem to win. EVER. On one holiday, we played 10 times and lost every game.

Here’s the question: was that actually unlucky? Should I have expected to win at least 1 out of 10 games?

I decided to have a think about how good my chances of winning the game are. The game boils down to turning cards over in a chain, and to win you need a King to be the last card in the chain. Suits are ignored, so the probability of winning is 4 (the number of Kings) out of 52 (the number of cards), or 1 in 13.

(If you’re not convinced by this handwavey argument, see the stack exchange thread. One contributor posts a coded version of the game which suggests 1/13 is correct).

This is all the information we need in order to see how unlucky, or otherwise, I was on holiday.

The probability of winning one game is 1/13, or about 8%. The probability of losing is 12/13, or 92%. That’s pretty high. But what about if you play more than once? If you play 10 times, can you expect to win at some point?

We’re interested in the probability of winning at least one game out of a given number of games, $N$. This would be very tricky to calculate directly, but fortunately there’s a way around it. The chance that I win zero times out of $N$ games, i.e. the probability that I lose every time is:

\[P\left( \text{lose all } N \text{games} \right) = {(\frac{12}{13})}^{N}\]

This is because each game is independent of the others – whether I win or lose one game has no bearing on the outcome of the next (assuming I shuffle the cards properly in between games). This means I can multiply the probability of losing each game together. So, if I play twice:

\[P\left( \text{lose both games} \right) = P\left( \text{lose game 1} \right)\ \times P\left( \text{lose game 2} \right) = \ \frac{12}{13}\ \times \ \frac{12}{13} = \ {(\frac{12}{13})}^{2}\]

If I played 3 times, the probability I lose every time is 12/13 x 12/13 x 12/13, or (12/13)³, and so on.

I then use the fact that either I lose every single game, or I win at least once. Exactly one of these statements must be true. Their probabilities must add up to one, as it is certain one or the other will happen:

\[P\left( \text{lose every game} \right) + P\left( \text{win at least 1 game} \right) = 1\]

So,

\[P\left( \text{win at least 1 game} \right) = 1 – P(\text{lose every game})\]

\[P\left( \text{win at least 1 out of } N \text{games} \right) = 1 – \ {(\frac{12}{13})}^{N}\]

For $N = 10$, this comes out as 55.1%. So I could at most be described as slightly unlucky on holiday – the odds were slightly in favour of me winning at least one game, but only just. In order to be pretty confident that I’d win at least one game, I’d need to play even more times.

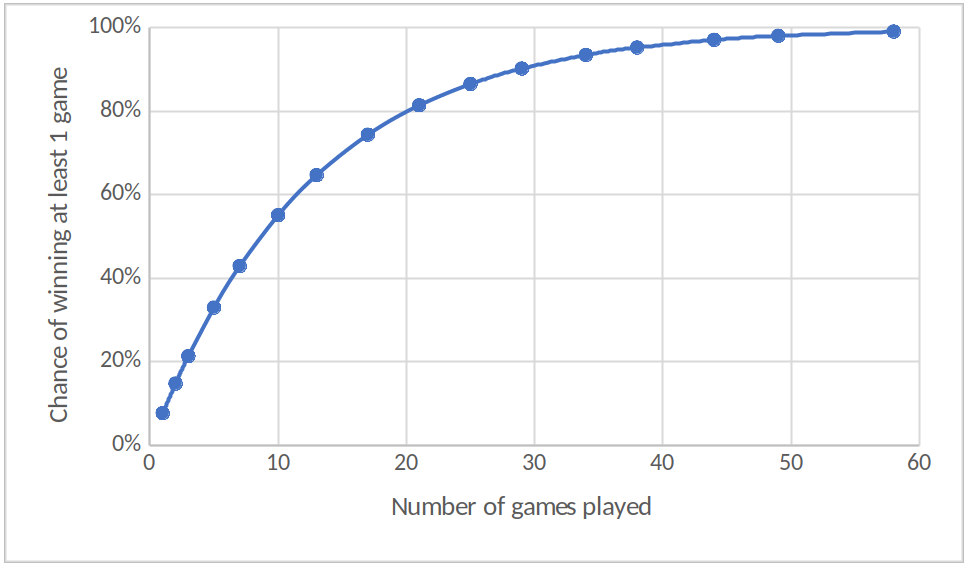
Here’s a chart of how the chance increases with the number of games. To be 90% sure of winning at least one game, I’d have to play 29 times. To be 99% sure, I’d have to play a whopping 58 times! That would certainly require some patience…

So, which bit of maths made you say “Aha!” the loudest? Vote:

 Loading ...

The poll closes at 9am BST on Saturday the 23rd.

If you’ve been inspired to share your own bit of maths, look at the announcement post for how to send it in.

This might be the last match of this year’s Math-Off, unless someone (maybe you!) sends in more pitches. Thanks for reading, and thanks for playing!