We invited guest author, Big Math-Off contestant and recent maths graduate Brad Ashley to review Immersive Math’s linear algebra textbook – a new take on the format.

Immersive Linear Algebra is an online interactive linear algebra textbook, created by mathematicians and computer scientists Jacob Ström, Kalle Åström, and Tomas Akenine-Möller. With their impressive collective knowledge of the field, and its applications within computer graphics, they seek to improve upon the idea of a textbook with the use of interactive diagrams.

First released in 2015 with four chapters, Immersive Linear Algebra has been updated over time to its now complete ten chapters. From scalars to eigenvectors, the authors take the reader on a journey through the basics of linear algebra.

A Twist On A Traditional Textbook

This online textbook is based on the belief that since we often use figures and diagrams to better our learning and understanding of new material, making these interactive will further this understanding. The authors argue this by means of example, presenting a variety of ‘interactive illustrations’ for different key ideas in linear algebra.

This ranges from graphically displaying a linear mapping of a single vector – variable by the user – to a game of breakout, demonstrating the direction of a vector. The intent is for the reader to gain a more intuitive understanding via better visualisation – ‘easier and faster to digest (linear algebra)’, as the authors put it.

This textbook utilises the ability of modern technology to present these interactive graphs, often 3D, which would have not been possible a couple of decades ago, in the hope of impacting how learning is conducted.

The authors begin with a short section on notation and trigonometry to potentially catch the reader up on what they need in order to learn the following content. The textbook is then divided into nine chapters, with subsections each dedicated to a specific part of the field.

This includes, but is not limited to, chapters for introducing the notion of a vector, the vector product, matrices, and concludes with Chapter 10 covering eigenvalues and eigenvectors. Each chapter opens with a motivating applied example – for example, Chapter 8, which covers the rank of a matrix, shows how eight fixed microphones detecting an audio source can be used to map its position in 3D.

This structure is certainly a strength of the textbook, and allows you to easily find theorems and definitions within each chapter. The main strength, though, is the interactive illustrations.

What Makes It Different?

These interactive diagrams are what make this online textbook unique. They seamlessly take their place alongside the narrative, applying context and a visual aid to the definitions, theorems, and examples. Each figure is accompanied by a short caption.

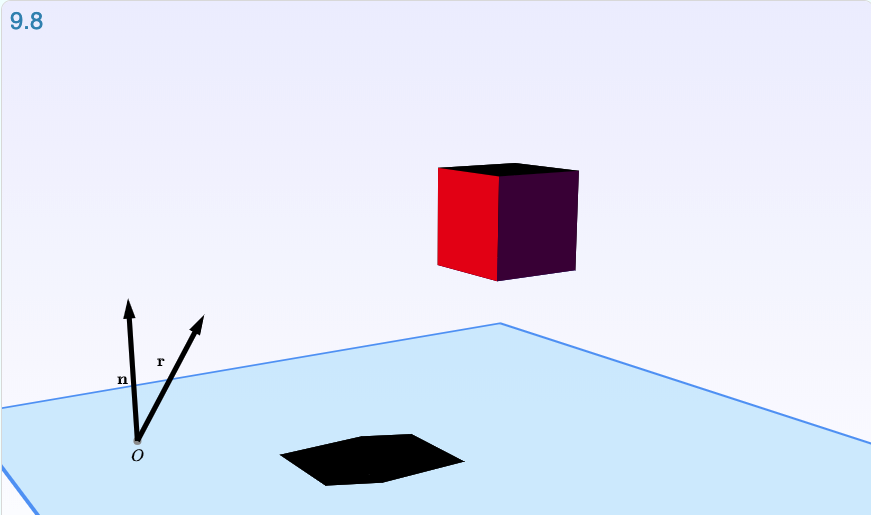
Some of the figures progress through multiple states, and impressively, the captions progress with them, explaining exactly what is happening between each step. This allows the reader to follow along, gaining insight to the mechanics behind the mathematics, and to jump between the steps at their own pace. A good example of this is Interactive Illustration 9.8, where the authors show how linear mappings can be used to create shadows for a cube in a 3D environment.

The main strengths of this interactive textbook certainly lie in its potential for newcomers to the field, i.e. to students. I remember distinctly that when I was first learning linear algebra, while I could handle the equations and raw mathematics behind everything, visualisation was somewhat of a struggle. This is where this textbook shines.

Beginners are taken on a journey through the basics, hopefully grasping foreign concepts much quicker and improving intuition of the mathematics behind them. The raw text containing definitions, theorems and proofs is written with clarity and consistency. With this, and accompanying informative but also interesting examples, the authors present an enjoyable introduction to linear algebra.

Missed Opportunities

A slightly clunky UI and occasional awkward sentences are worth noting, although do little to sour the experience. More frustrating, however, is the less-than-preferable amount of pure mathematical engagement. Besides the odd line of ‘this is left as an exercise for the reader’, there seem to be missed opportunities to engage the reader in some of the mathematics.

This is more apparent than it otherwise would be, since the interactive figures succeed so well in getting the reader enthused. Many of the proofs, especially the shorter ones, seemed perfect opportunities for the reader to exercise their newfound knowledge, but instead a full proof is given.

This is slightly made up for by an option not to show the proofs in the preferences menu, tucked away in the corner – however, this could have been emphasised more, to encourage the reader to get involved with the equations themselves.

Worth Checking Out?

Immersive Linear Algebra does not reinvent the way we learn, but feels like a logical progression from the concept of a textbook. Its interactive illustrations improve upon the idea of a diagram, allowing for greater insight into the underlying mathematics.

While it could give more encouragement to get the reader to play with the mathematics themselves, this online textbook is certainly something I would have liked to have access to when first learning the field, for its unique take on what a textbook can be. I would recommend that anyone wanting to learn linear algebra should consider taking a look!