Equatum is a new puzzle format invented by mathematician Justin Roughley, and is now available in the form of a book. We chatted to Justin about his life and his puzzles.

Hi Justin! Please tell us about yourself.
Life has led me through maths, puzzles (Martin Gardner in Scientific American in the 1970s), software (real-time through to functional), electronics, meditation, Buddhism, vegetables, wildness, financial analysis, financial forecasting, data analysis, games & puzzles. I love to explore where disciplines overlap. And I’m the inventor of Equatum Puzzles!
What are Equatum puzzles?

Equatum is a new type of puzzle which involves equations. Solving them requires a mix of logic and arithmetic. These puzzles are unusual because at least one of their unknowns could be a number OR an operator ($+−\times\div=$). I’m not aware of any other puzzles or problems which have this property but if anyone knows of some, I’d be interested to hear about them. To make this clearer, it helps to consider various types of problems:
In arithmetic problems such as $2\ +\ 3\ =\ ?$, and algebra problems such as $3 \ \times\ ?\ −\ 5\ =\ 7$, the unknowns are all numbers. In “Operator search” puzzles, like $3\ ?\ 2\ ?\ 5\ =\ 11$, the unknowns are operators ($+−\times\div$). Is it $3\ +\ 2\ \times\ 5$ or $3\ −\ 2\ \div\ 5$ or…?
In Equatum puzzles the unknowns can be a number OR an operator ($+−\times\div=$).
Here’s four examples:
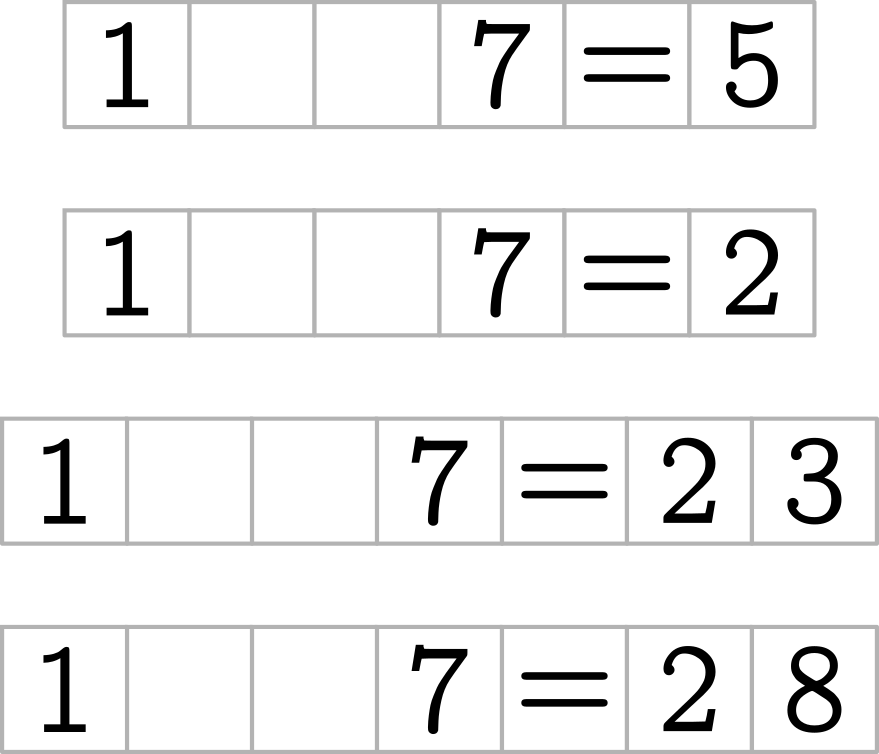
In each of these you need to enter one of these symbols: \[1\ 2\ 3\ 4\ 5\ 6\ 7\ 8\ 9\ 0\ +−\times\div=\] into each cell so that the result is a balanced equation. If you try these then you’ll see that even for these relatively simple puzzles you need to think a bit differently from other problems.
How did you get the idea for these puzzles?
The initial idea for Equatum came in 2015 in an unusual way. I was thinking about relationships between people: sometimes we don’t understand people; sometimes we don’t understand the relationship. The ‘aha!’ moment was when I wondered what happens when you don’t know which is the person and which is the relationship. So rather than unknown people and unknown relationships, you just have unknown which might be a person or a relationship. I’m aware this is a bit abstract!
Being interested in Maths, I wondered what this would mean when applied to equations. The analogy is that the people become numbers and the relationship becomes an operator, because that’s the relationship between the numbers. So following the analogy, we need unknowns which can EITHER be a number OR an operator ($+−\times\div=$). Thus Equatum was born.
Subsequently I’ve reflected on what led me to think in this way and a couple of things spring to mind: I am a Buddhist, and some Buddhist teachings explore similar territory – in particular the four levels of sunyata or emptiness.
Also, a few years ago I learned the programming language Haskell. This is a purely functional language, and in such a language we can think of numbers as functions which have no inputs and one output: the value of the number. Considering this type of functional approach made me consider that numbers and operators are not as different as they might seem.
Are there other types of Equatum?
There’s examples of some different sorts of Equatum below. Some of them include more than one operator in a calculation. When this happens the usual rules of BODMAS apply: first calculate division and multiplication from left to right, and then calculate addition and subtraction from left to right.
In the following Equatum, one of the unknowns is the equals symbol:
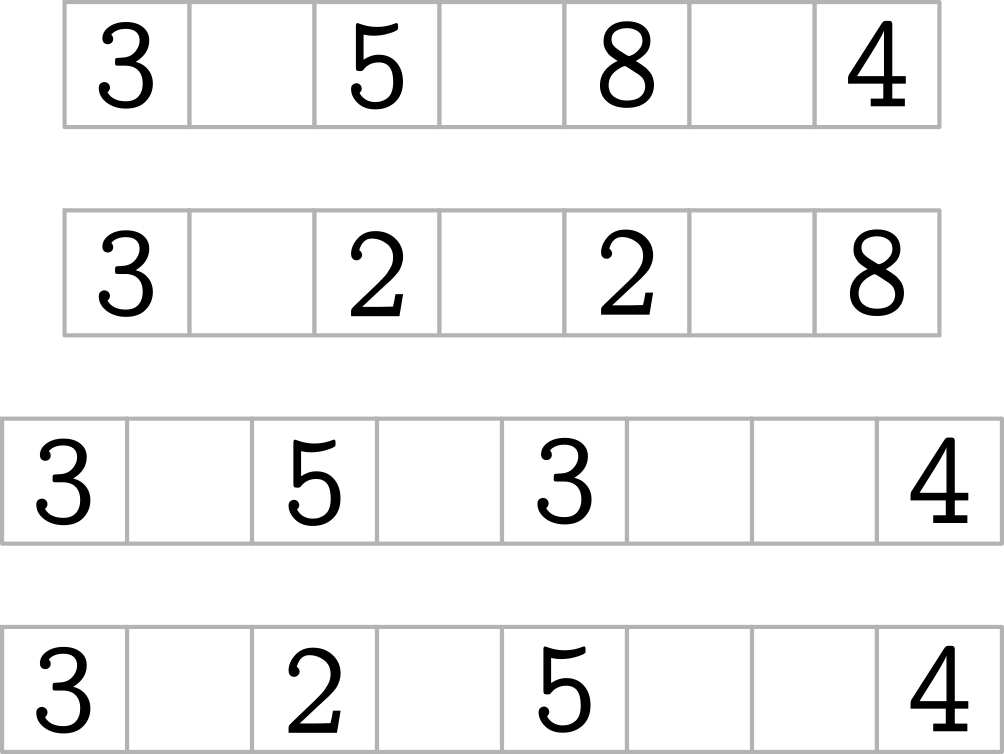
As before, you need to enter one of these symbols: \[1\ 2\ 3\ 4\ 5\ 6\ 7\ 8\ 9\ 0\ +−\times\div=\] into each cell to form equations.
The next ones are a bit different. In these you are given all the symbols and you need to find their order:
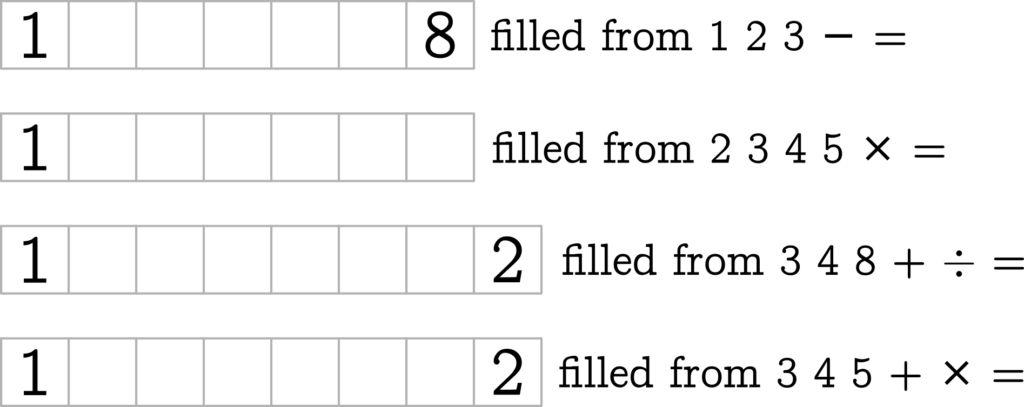
You need to slot the symbols from the right into the cells on the left in the correct order so that they form an equation. Only use each symbol on the right once.
And continuing this theme of finding the right order of symbols, this idea is extended to a grid like a crossword with clues:
| Across 1 Arrange 1 6 7 + = 4 Arrange 2 3 5 + = 5 Arrange 1 3 4 + = Down 1 Arrange 3 4 7 + = 2 Arrange 1 2 3 + = 3 Arrange 1 5 6 + = |
You need to find the right order for the symbols to form equations in the across and down directions.
How can people try the puzzles for themselves?
The samples above provide a taste of some Equatum puzzles, and the Equatum website has a few sample puzzles.
The book of Equatum Puzzles came out in October, and contains 100 of the grid-style Equatum. These are hand-selected and sorted into increasing difficulty, so they go from fairly simple up to diabolical. The book is available through the website or at getbook.at/EquatumPuzzles.
What’s your favourite Equatum puzzle?
My favourite Equatum puzzle is the word CLEVER. This is yet another form of Equatum in which the equation has been encoded. Each letter represents one of the symbols $1\ 2\ 3\ 4\ 5\ 6\ 7\ 8\ 9\ 0\ +−\times\div=$ such that the same letter always becomes the same symbol, and different letters always become different symbols. There’s only one way to replace the letters such that the result is an equation.
What I like about this puzzle is that the starting point is a word and the end point is a simple arithmetic equation – both very familiar to most, but the logic and thought process to get from one to the other is unfamiliar. I think this Equatum is a very succinct introduction to the experience of solving an Equatum.
A close second would be puzzle number 71 from the Equatum puzzles book. It’s a $7\times7$ crossword-like grid whose solution has just the symbols $1\ 2\ 4\ 8\ 9\ \times\div=$ as eight short intersecting equations. Again, it’s a relatively simple starting and ending point but turns out to be a fairly challenging puzzle.
Do you have any top tips for people trying to solve the puzzles?
Often the challenge of Equatum is that there are so many possibilities that it will take too long to search through them, so a useful approach generally is to find techniques that will reduce the number of possibilities to a small enough number that can be checked. It’s not always obvious how this can be done, but with some ingenuity and careful thinking these techniques can be found.
Different types of Equatum sometimes need different techniques. The largest number of Equatum out there are in the Equatum Puzzles book, and all those puzzles are grid Equatum (i.e. the ones which look like a crossword), so I’ll give some tips for solving that type of Equatum:
A good first step is to look at the crosspoints (i.e. the intersections of equations across and equations down) and find the symbol, or at least the range of possible symbols for each of these cells.
It’s usually best to solve the easier equations first, and to work out which are easier consider the following:
- Shorter equations are generally easier than longer ones
- Equations with single digits are generally easier than ones with multi-digit numbers (i.e. above 9). Note that counting the number of digits and non-digits in an equation can establish whether there are any multi-digit numbers.
A couple of more advanced tips:
- For equations which only have single digits and the $+$ operator, adding up the digits and dividing by two tells you what each side of the equation adds up to and this can help establish some digits.
- When equations have numbers involving more than one digit (i.e. greater than 9), considering modulo 10 arithmetic can help find solutions.
Anything else to add?
I hope people find as much pleasure solving these puzzles as I did creating them and I’d encourage anyone who has any questions about solving them to send me a message via the website. And lastly – thanks very much to the Aperiodical for posting about this – much appreciated.
Hello,
can we use several times the same symbol in a given equation?
For example, can 1+1=2 be a solution to : * + * = 2 ?