At the 2021 UK MathsJam Gathering, I gave a talk on a subject that has bothered me more than is reasonable: the graph-theoretic layout of the narrative of the baby’s book Each Peach Pear Plum, by Janet and Allan Ahlberg.
It’s one of my son’s favourite books to fall asleep to. It was his older sister’s favourite, and mine and my wife’s when we were little. I agree with the quote on the back cover, that it’s “the perfect first book”.
BUT
Every time I read it, a thought pops into my head that dampens my enjoyment: an incompleteness, like noticing your coat is missing a button, or one book on a bookshelf is taller than the others.
Basically, I had to give this talk in order to stop the quiet voice in my head that requires Order In All Things.
So, here’s the recording of my talk.
The slides are on my homepage, in case you want to look through them more slowly.
After I had the idea, I wasn’t sure if this was a maths talk. While making up my “improved” poem, I realised that it is.
In order to make the story follow the complete graph, I needed a page from character $x$ to character $y$, for each distinct $x$ and $y$.
So I opened a spreadsheet and typed them out. Each character will appear on eight pages: four where they are the “I spy”, and four where they do something rhyming with their name.
After writing out four rhymes for each character (actually three – I reused the original rhymes from the book) I needed to work out the order they appear.
It turned out this is harder than I thought! I assumed that I could just do this:
- Draw out a 9×9 grid, where rows represent the first character on a page, and columns the second character.
- Erase the diagonal, because you don’t have a page with the same character twice.
- Start at the first row, second column: $(i,j) = (2,1)$.
- Pick the smallest $k$ such that $(k,i)$ hasn’t been visited yet.
- Mark $(k,i)$ and $(i,k)$ as visited.
- Repeat steps 4 and 5 until every cell has been visited.
I tried this, and quickly got stuck with no valid options for the next page, but several unvisited cells.
So I did some thinking. I want to avoid ending up with no choices, so I thought I could put that off by picking the column with the most options left.. That worked! I don’t know if it’s guaranteed to, but I think it is. If I wasn’t spending so much time reading stories to babies, I could maybe write down a proof!
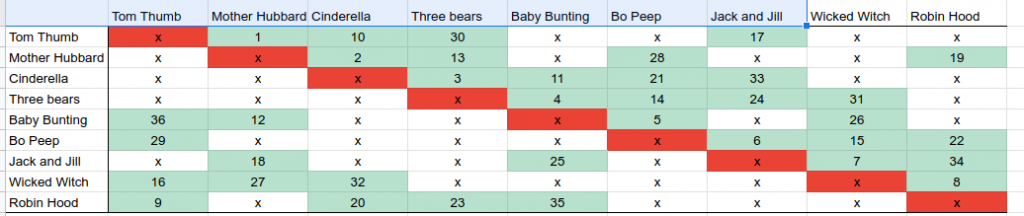
I’ve made an interactive thingy to try filling out a grid. Have a go, and see if you can come up with an algorithm to fill it all.
Each time you click on a cell $(i,j)$, it marks that cell and $(j,i)$ as visited, and both cells are filled in with their position in the sequence. On your next move, you can only pick a cell from the row corresponding to the column the last cell was in.
It starts with the lines from the original book filled in, though you can undo those if you want to start a different way.
So hopefully, now I’ve scratched this mathematical itch, I can again enjoy this book as much as the baby does. Maths as therapy.
Nice! I also have a mathematical beef with a very similar-sounding (though mathematically very different) children’s book, Orange Pear Apple Bear. Perhaps I should write about it.
In any case, you are trying to find an Eulerian cycle in a complete graph. According to a theorem of Euler + Hierholzer, this is possible iff the number of vertices is odd (and hence the vertices all have even degree). The only way you can get stuck is if you revisit the same character too many times and run out of edges incident to them, so it definitely works to always visit least-visited character at each step. Alternatively, you can use Hierholzer’s algorithm: just proceed randomly until you get stuck (which is guaranteed to be at the character you started with); then restart at any character that is still incident to missing edges and proceed randomly until you get stuck again, splice the resulting cycle into your original cycle, and repeat until you have visited every edge.