This semester I’ve been teaching a module that covers a couple of different maths topics, and have been setting little puzzles for my students to complement what they’re learning – and some of them have been quite fun to write and play with. I thought I’d share some of them here, so you can enjoy them too.

Complex numbers and functions

The module covers two topics, the first of which is complex numbers and functions. I thought I’d give them some practice at adding and multiplying complex numbers using this variant on the four fours puzzle I found on a blog post by David Butler:

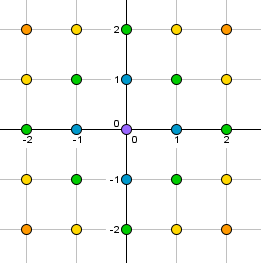
Using any of the operations +, -, ×, ÷, as many brackets as you want, and as many of the complex number number i as you need, find a way to make each of the numbers a+bi for a, b = -2, -1, 0, 1, 2.
How does your answer change if you are not allowed to use the – symbol?

As well as being a nice puzzle to play with, solving this will hopefully serve as a good refresher on how complex addition and multiplication works – particularly given that additional constraint.

Since a later lecture considered conformal (angle-preserving) maps, we introduced a definition of the angle between two lines when both the lines aren’t straight. I was reminded of this tweet by Kit Yates about some slightly controversial maths homework:

For a 7-year-old, there’s apparently an obvious answer to this, but to anyone who knows how to define the angle between a line and a curve, it gets a bit more complicated. The challenge for my students (who are also training to be secondary maths teachers, so will have to get used to this kind of ambiguity) was to answer the question with both ‘true’ and ‘false’, explaining their answer each way.

For a chance to play around with complex transformations and mappings, I assembled a dot-to-dot puzzle set in the complex plane. Starting from a given point $P_1$, each subsequent point was defined in terms of the previous, and the result should be a familiar shape.

Having created a GGB file of the solution (warning: spoilers!) it turns out it’s then quite pleasing to drag the point $P_1$ around and see how it deforms the shape.

And to finish off the complex numbers content, I couldn’t resist borrowing this classic from Matthew Scroggs’s excellent website:

For which complex numbers z are \(\operatorname{Re}\mathopen{}\left(z^2\right)\mathclose{}\) and \(\operatorname{Im}\mathopen{}\left(z^2\right)\mathclose{}\)  both positive?

Cryptography

The next section of the module covers some techniques in cryptography, which includes some basic ciphers up to RSA encryption.

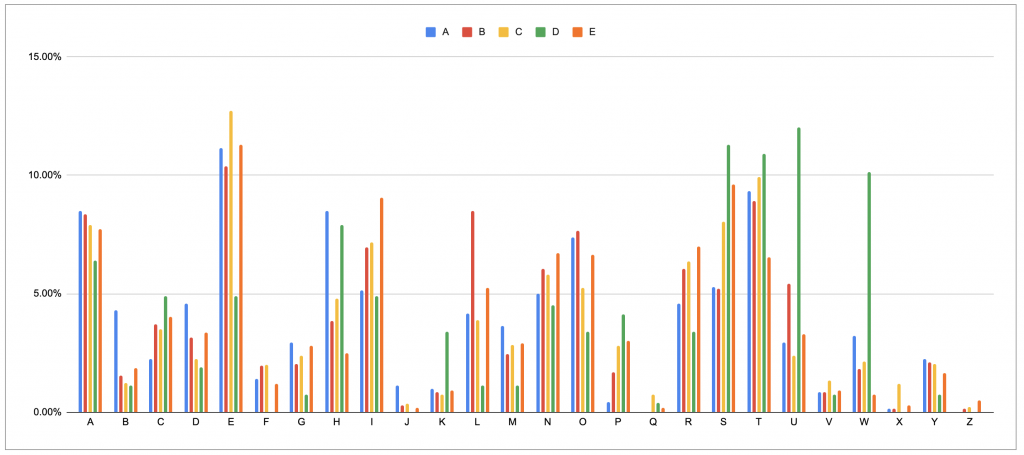
I put together (what I think is) a lovely frequency analysis puzzle, giving an insight into how frequency charts might vary depending on the type of text being encoded:

The graph below shows the relative frequencies of different letters of the alphabet in five different pieces of text. (If you’re unable to view the graph, here’s the raw data as a spreadsheet.) Can you identify which text source is which?

Sources:
1. The text of the Wikipedia article on Frequency Analysis
2. The official UK Scrabble wordlist
3. A page from the ‘L’ section of a dictionary
4. The text of the Lewis Carroll poem ‘Jabberwocky‘
5. All the URLs linked to from the front page at SHU.ac.uk

To accompany a session on the Enigma machine, I thought I’d give students a chance to play around with the kind of combinatorial questions raised by the Enigma plugboard:

If there are 26 holes in a box, each of which can have one end of a wire plugged into it, how many possible ways can I use a single wire to connect two holes together? What about if I have two (identical) wires?

The next session of the module covers modular arithmetic, the Euclidean algorithm and invertible elements in $\mathbb{Z}_n$. As part of this, there’s a brief discussion of Diophantine equations and Bezout’s identity, which was as good an excuse as any to set this puzzle from Die Hard 3 (warning: contains a bunch of swearing).

Try to reconstruct their full solution from the clips shown (the film cuts away, so you miss three steps – one is emptying a full jug, another is pouring the contents of the other jug into it, and a third is filling an empty jug). You may find it helpful to use a column for each of the two jugs, and after each step, record how much water is in each jug.

If filling an empty jug from the tap counts as +1 of that jug, and pouring away a jug’s worth of water (and assuming any water not used as part of the solution at the end is poured away) counts as -1 of that jug, can you write down an expression for this solution in terms of the number of times each of the two jugs are used? Can you see how this relates to the sizes of the jugs in gallons?

While we were talking about modular arithmetic, I thought I’d try to come up with a puzzle around the structures found in these groups for different orders, which involves identifying which columns will follow which patterns.

Make a copy of this Google spreadsheet and complete the puzzle given there, which concerns multiplication tables in modular arithmetic. What patterns can you see in the structure of the completed table?

Coding Theory

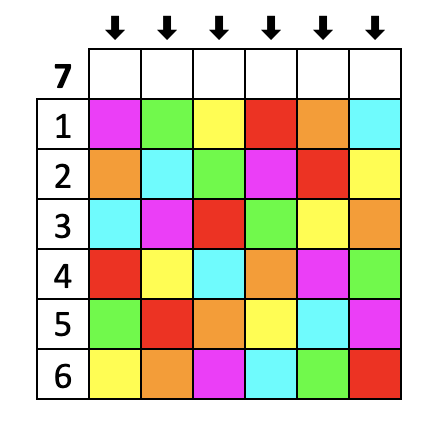
For the section of the course on coding theory, we discussed error correcting codes based on binary words, and I thought it was a good excuse to share a photo of my ludicrous bathroom floor, which we got tiled with a hilarious and appropriate message in binary. The puzzle was stated as:

Katie’s bathroom floor has a secret message encoded in it.

Assuming the message is in two columns running from
top to bottom in the photo, can you work out what it says?

The message contains one error. Can you find which tile is
incorrect, and say what colour it should be?

And finally, while on the topic of error correction, I spent far too long coding a Python script to search within a wordlist for sets of words which differed in a single position in order to generate a good question for this puzzle:

Considering the list of words below as the entire set of allowable words, draw a graph with each word as a node, and an edge joining two words if they have Hamming distance 1.

bead, bean, bear, been, bran, dean, dear, jean, lead, leaf, lean, loan, mean, moan

Use your graph to answer the following questions:
– The message ‘dean’ is received, and it is known that the transmission contains exactly one error. What could the original transmission have been?
– The message ‘dean’ is received, and the transmission contains up to two errors. What could the original transmission have been?

I hope you find some of these puzzles mildly diverting! I had fun putting them together, and I have documentary evidence that at least one of my students actually had a go at one of them.