It’s nine years since the first integer sequence review, and six years since the last one. We’ve grown as people, and in CLP’s case, grown people. The world has changed, but our love for the Online Encyclopedia of Integer Sequences hasn’t.
A101544
Smallest permutation of the natural numbers with $a(3k-2) + a(3k-1) = a(3k)$, $k > 0$.
1, 2, 3, 4, 5, 9, 6, 7, 13, 8, 10, 18, 11, 12, 23, 14, 15, 29, 16, 17, 33, 19, 20, 39, 21, 22, 43, 24, 25, 49, 26, 27, 53, 28, 30, 58, 31, 32, 63, 34, 35, 69, 36, 37, 73, 38, 40, 78, 41, 42, 83, 44, 45, 89, 46, 47, 93, 48, 50, 98, 51, 52, 103, 54, 55, 109, 56, 57, 113, 59, 60
DC: This looks like arbitrary nonsense. What does it mean by “smallest permutation”?
CLP: I’m writing this down… oh wait, does zoom give us a transcript? Let’s just talk and get Zoom to write it down.
DC: I tried to turn it on. It said I could ask for permission anonymously.
CLP: “Someone is trying to turn on captions…”
An excerpt from later in the transcript:
01:17:05.550 --> 01:17:11.610 David Cushing: The number of simply elders over the field of two elements is not in the EU is. 01:17:15.450 --> 01:17:16.830 David Cushing: Where paradigm mentioned. 01:17:19.890 --> 01:17:20.280 Christian Lawson-Perfect: Okay. 01:17:25.110 --> 01:17:36.330 David Cushing: So cozy was evil 101 then we get to, and then it was one one, and then we don't know we all knew what damage and nine.
Automatic transcription has a long way to go.
DC: I shouldn’t read out what it’s saying. We’ll end up with sort of Chinese whispers.
CLP: That would be a fun game. I bet someone in an art gallery is reading out their Zoom transcription on a loop.
DC: “Smallest permutation…” So is the point that this relation could spawn many sequences?
CLP: Yeah. Is “smallest” lexicographically earliest?
DC: How many things do we need to generate it? Two? No, we need lots of terms because… oh, I’m confused.
CLP: Is there an example?
DC: No, we just need two terms.
CLP: Right. So, this is one I came up with independently. I’ll try and reconstruct my thought process. I think the idea of writing it in three columns is what I did. You write down the first two numbers you can, and add in their sum afterwards.
DC: Right! Now I’m just reading what the question is, and I don’t know what it means.
Question: in which column ends up the repdigit $R_m(d)$ with $m$ times the digit $d$?
Answer: $R_m(d)$ will be in:
1) column 1 if d = 1, 4, 6, 8, or if d = 9 and m is even;
2) column 2 if d = 2, 5, 7;
3) column 3 if d = 3, or if d = 9 and m is odd.
DC: Who worked that out? Who thought to check where the repdigits go?
CLP: It feels like you shouldn’t be able to say anything about repdigits in this.
DC: The graph is nice. Did you look at the graph?

CLP: Yeah! You alternate between two small bits together and one big bit on the larger line. What’s the gradient of the line?
DC: I still want to know why it says “smallest permutation”.
CLP: I think it’s lexicographically earliest. That would make sense to me. So you always take the two smallest numbers you can, satisfying the condition. The condition is, you take two numbers you haven’t written down yet, then write down their sum.
DC: Have you been to the next sequence? A101545.
CLP: Whaaaat? The inverse! What does that look like on the graph? Can I guess?
Morally, the line should be going the other way, but that’s impossible. Oh! On
the pin plot, the pattern isn’t the same: on the lower line it’s just ones,
but on the upper line they’re in groups of threes, fours and fives.
DC: You know how the finite symmetric groups are finitely generated? What
about the infinite one?
CLP: They’re two-generated, I think. Did you tell me this?
DC: Yeah, if you’ve got a pack of cards, the two moves are swapping the top
two, and moving the top card to the bottom. But it’s hard to move the top to
the bottom if you’ve got an infinite number of cards.
CLP: So is $S_\infty$ finitely generated?
DC: Is that what it’s called?
CLP: I assume so. What am I, a group theorist? My guess is it’s not two-generated.
DC: Have you got a proof?
CLP:
DC: Oh, it’s clearly false, isn’t it?
CLP: Can you say something like, the set of permutations of the natural numbers has the same cardinality as the reals?
DC: That feels wrong. Surely it’s generatable with countable things? Oh no, that’s fine. Anyway, what I was thinking was, you could pick two sequences on the OEIS that generate every other permutation, and you could write every permutation in terms of those. Have you seen how, on the one we’re looking at, if you perform this twice, you get A101546.
CLP: What? Why is that in? Who cares?!
DC: It gets worse! Go to A101547, Christian.
CLP: OK, the graph now has three lines. Do we conjecture that you add a line each time you compose it? What’s next?
DC: They stop doing it after that. That’s a shame. Anyway, my point is, we could go to every entry and write down what it is as a product of those two.
CLP: I don’t think they like it when you do that.
DC: Are the natural numbers in but with 1 and 2 swapped? They are!!! A181440.
CLP: “Auto sequence”? What does that mean? We’re getting distracted.
DC: Right, back to the sequence review. What are the four categories? Style, control, damage and aggression?
CLP: Is that what we did?
DC: No, that’s Robot Wars.
CLP: The four categories are: Novelty, Aesthetics, Explicability and Completeness.
DC: Novelty?
CLP: Your reaction on seeing it was, “not another permutation”.
DC: But this might be the smallest!
CLP: That’s the natural numbers, isn’t it?
DC: Oh, that counts as a permutation, doesn’t it?
CLP: Never forget your identity, David.
DC: Since there’s infinitely many permutations, does it have to get zero?
CLP: No, because it’s a nice rule!
DC: It is a nice rule.
CLP: OK, because I try and add sequences to the OEIS — have you added any
recently?
DC: Not recently :(
CLP: I’m now trying to tick off one of each kind of sequence. You have ones like, there’s a rule for generating the next one, numbers with a certain property, and so on. But I want to get a permutation of the natural numbers, and I haven’t done it yet, so I keep looking up permutations. Every time I look up a nice one, it’s already in.
DC: I’m going to look at the code.
CLP: There’s only Maple and Mathematica.
DC: It’s a bit Fibonacci-like, isn’t it? All Fibonacci-like sequences have a formula
involving $\sqrt 5$. What’s making it not grow?
CLP: Because you’re not using the previous sum, you’re just using the next
thing along, so it grows linearly.
DC: But there’s a recurrence relation in the title! Is that just not true?
CLP: It’s a recurrence relation of three parts, and they don’t overlap.
DC: Ahhh! I suppose that makes it more novel. Who’s Bernard Schott and why does he have his own page?
CLP: He’s all over the place, Schott. I feel like there’s an absolute tonne of them from 2004. Something happened, and I don’t know what.
DC: You know how lots of sequences get rejected? We need a version of the viXra.
DC: Oh my god, there’s more sequences. A249031: the non-anti-Fibonacci numbers.
CLP: Well, this is the one we should be reviewing!
DC: So is this a smaller permutation?
CLP: No, because it doesn’t have the same property A101544 does. And anyway, the other one starts 1,2,3 and this one starts 1,2,4. The anti-Fibonacci numbers gives you the numbers on the upper line in the one we’re reviewing. So Douglas Hofstadter came up with this rule and wrote down this convoluted definition of it, and thought that was the interesting sequence.
DC: Who is Douglas Hofstadter?
CLP: He’s the Gödel, Escher, Bach guy.
DC: What Novelty should we give it?
CLP: I’m going to give it a cool 4/5.
DC: Aesthetics: the table’s pretty. I like the stupid thing with the elevens, and hundred-and-elevens.
CLP: Can we talk briefly about how in the references there’s someone called Loren Larson? And George Gilbert. GG, LL, and Mark Krusemeyer letting the side down.
DC: We can change it.
CLP: Oh, they get so cross with you when you change things. Hey David, where does the all 7s sequence come in it?
DC: Ooh, what was the sequence that was all 3s, but with one 1?
CLP: Have a look at A122553.
DC: This is not the sequence I’m thinking of!
CLP: In the comments, the first fact it mentions is that it’s the continued fraction for something involving sqrt 13. That’s not what I would say about it!
DC: Look at its generating function!
CLP: Are you talking about $3-2 \times 0^n$? Wait a minute! It says the first index is 0, so it’s saying that $0^0 = 1$.
DC: It is, right?
CLP: It’s not! It’s undefined, you can pick.
DC: The other day, I picked that it was 1.
CLP: I don’t like it. There’s some serious hi-jinks going on in this sequence. I didn’t think you could make a mistake in this entry, but someone has.
DC: There’s a mistake?
CLP: $0^0$ is not 1! Or if it is, then it’s also everything else.
DC: That’s a beautiful formula.
CLP: I hate it.
DC: Have you seen that weird infinite sum?
CLP: That’s just saying it’s a decimal representation of something. Why is this entry so weird?
DC: Have you seen that funny product as well? That doesn’t even use the sequence, it’s just another fact about 4/3!
CLP: Added in 2021. Who are you, Amiram Eldar?
DC: Have you seen the Pari code?
CLP: Well, there you go, that’s better.
DC: Let’s look at the graph.
CLP: Are you hoping for a bug in the OEIS’s plotting code? I dislike it entirely. I’m going to mark it low on everything.
DC: But we’re not reviewing it.
CLP: We need to do a drive-by review of this one.
A122553
$a(0) = 1$, $a(n) = 3$ for $n \gt 0$.
1, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3CLP: How can you like the aesthetics of it? It’s like an enormous blank wall with a single smear of poo on it.
DC: I’m knocking one off Explicability because there’s a 1 there. What does the offset mean? It says 0, so you start at $n=0$, but what does the 2 mean?
CLP: The form that you use to submit a sequence doesn’t say what the second number in the offset is for.
DC: Completeness: there isn’t enough room for all the 3s because it’s used the first position for 1.
CLP: I’m going to heavily disagree with what you just said.
DC: “Sequence in context” often has nothing to do with it, doesn’t it?
CLP: I have no idea about how that works. The sequence before in the “sequence in context” is something that alternates between 3 and -3. – Wait, look at the Mathematica for A122533.
DC: What the hell’s that?
CLP: The digits of 4/3, in base 10, but only 105 of them. That seems
arbitrary. Is that how many there are in the entry? Pure dross. I’m going to
mark it down on Completeness just because of the Mathematica code.
DC: The continued fraction’s weird, I don’t like it. There’s a 2 in there.
CLP: Want to revise your Aesthetics score?
DC: Yeah, I’ll give it 4. The fraction would be beautiful if there wasn’t a 2.
| Novelty | Aesthetics | Explicability | Completeness | |
| DC | $\frac{5}{5}$ | $\frac{4}{5}$ | $\frac{2}{5}$ | $\frac{4}{5}$ |
| CLP | $0$ | $0$ | $\frac{2}{5}$ | $\frac{5}{5}$ |
DC: Oh-ho-ho! I’ve got another sequence for you, and you’re not going to like it. A290858.
CLP:
CLP: I’m glad Zoom echoed that sigh back at me, because I needed mechanical assistance to express how I feel.
DC: Look at the title of it, though!
CLP: It’s one of those things where you sort of gesture wildly, and when you try to write it down you end up with this three-line monstrosity.
DC: Look at the Mathematica code!
CLP: If Mathematica can do one thing, it’s “have built-in functions for cellular automata”. Why isn’t this a single function?
DC: Right, I’ve got one more sequence before we go back to reviewing. A157831.
CLP: It’s like Where’s Wally, but for 4. Oh, there are two! Are they growing?
DC: Look at the graph.
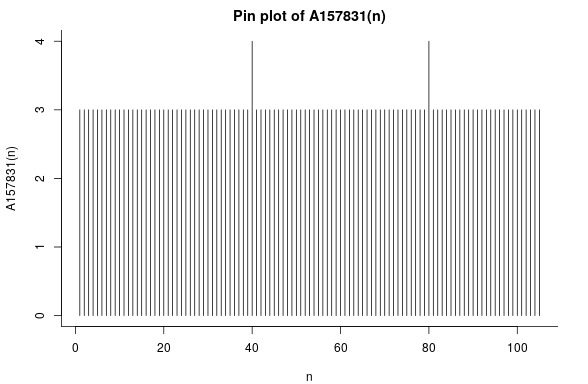
CLP: This sequence is flicking the Vs at me.
DC: I think we need to judge the Aesthetics of A101544. I like the table.
CLP: I like how there’s no obvious pattern to the numbers. It jumps about like good jazz.
DC: So where’s the all 3s sequence in this table? Column 3?
CLP: Yeah, and all 7s is in column 2. So we know which column they’re in, so if we split the sequence into three bits, we know which bit the all 7s repdigits are in, but that’s it. There’s a note in the formula section which gives the entries for each column. Stated without proof is that the two small numbers are always adjacent. I love to state things in the OEIS and not give a proof. It’s a work held to serious scholarly standards.
DC: I’ve just found the best thing ever. It’s a list of all the sequences that are permutations of the natural numbers. Whoah! Some of them are only conjectured‽
CLP: A064809: “Decimal expansion of π written as a sequence of positive integers avoiding duplicates”. So the conjecture is that everything eventually appears, because they’re all distinct by definition. Fair enough.
DC: Explicability: it’s easy to explain, isn’t it? I want to take a point away for being weird with the fact about repdigits. Does anything like this get proven?
CLP: There are no references here, are there, apart from this book we don’t have, A Mathematical Orchard, Problems and Solutions.
DC: Completeness: it does have every positive integer in it. That’s pretty complete. Is there a formula for it?
CLP: The formula line refers to other sequences, and those refer to the paper “Anti-Fibonacci Numbers: A formula“. This leaps out at me: “The utterly odd nature of an integer is the property of being, or not being, utterly odd.” Noted.
DC: Have you seen that it says that at least of 13% of Fibonacci numbers are anti-Fibonacci numbers?
CLP: Oh, so there is a formula, but it’s by cases, and it’s a bit fiddly. I’d say it’s complete. I can’t think of anything to add to it. It’s a permutation of the natural numbers, and we’ve got to respect that.
DC: I’ve found it! A051200. This is the one I was trying to find.
CLP: (╯°□°)╯︵ ┻━┻
Scores
| Novelty | $\frac{4}{5}$ |
| Aesthetics | $\frac{3}{5}$ |
| Explicability | $\frac{2}{5}$ ($\frac{4}{5}$ if nobody had written the repdigits fact) |
| Completeness | $\frac{5}{5}$ |
| Total score | \[ \frac{4+3+2+5}{20} = \frac{14}{20} = \frac{7}{10} \] |
DC: Apart from the natural numbers, what’s the smallest permutation in the OEIS?
CLP: I reckon with a quiet afternoon we could settle that.
A quiet afternoon of searching ensues.
CLP: David, look at sequence A257340. This is the grand slam! It’s conjectured
to be a permutation. It’s inexplicable. I’m getting this on a t-shirt, I’m getting it engraved in stone and cemented on the front of my house. This is deep esoteric knowledge.
. | -4 | -3 | -2 | -1 | 0 | +1 | +2 | +3 | +4 | +5 . ---+--------+----+----+----+----+----+----+----+----+---- . | . | +------------------------------------------------ . +4 | | 83 68 75 74 81 70 87 76 85 ... . ---+ | +---------------------------------------+ . +3 | | 66 | 49 38 45 44 51 46 53 42 | . ---+ | | +-----------------------------+ | . +2 | | 79 | 36 | 25 22 21 20 27 26 | 55 | . ---+ | | | +-------------------+ | | . +1 | | 64 | 47 | 18 | 7 8 9 10 | 29 | 48 | . ---+ | | | | +---------+ | | | . 0 | | 77 | 30 | 23 | 6 | 1 2 | 11 | 24 | 59 | . ---+ | | | | +----o | | | | . -1 | | 60 | 43 | 16 | 5 4 3 | 13 | 31 | 50 | . ---+ | | | +--------------+ | | | . -2 | | 73 | 40 | 19 14 15 17 12 | 35 | 57 | . ---+ | | +------------------------+ | | . -3 | | 62 | 39 34 33 41 28 37 32 | 61 | . ---+ | +----------------------------------+ | . -4 | | 71 56 69 67 54 65 58 63 52 | . ---+ +--------------------------------------------+
DC: We’ll have to give A101544 less points, by comparison.
CLP: Fair enough.
CLP: I’m going to start a religion. According to a law of fractions revealed to me in a dream by A257340, we have to take three off the top and use them to multiply the bottom.
\[ \frac{7-3}{10 \times 3} = \frac{4}{30} \approx 0.1333\ldots \]
DC: That’s the decimal expansion of a certain sequence.
CLP: Except it’s got a 0 in front of it. That entry is bafflingly wrong in so many places!
DC: I think we can agree that two sequences won today: A122533, and A257340.
CLP: Go in peace, David, and may all of your neighbours be coprime.
(the Zoom transcript ends with discussion of unwelcome places that hair grows out
of now we’re old)