My son and I visited The Mathematikum in Giessen. This is well worth a visit, we did it as a day trip by train from holiday in Frankfurt, which worked well because the museum is close to the railway station. The Mathematikum specialises in ‘hands on, minds on’ interactive activities, and we spent about 5 hours exploring the four floors. I enjoyed the open-access article The Mathematikum in Giessen by Martin Buhmann, who was kind enough to meet us and show us around.

There are some Mathematikum-made exhibits at MathsCity Leeds. I took some pictures of exhibits we had enjoyed that aren’t (to the best of my memory) available in Leeds. Here they are, in no particular order.

My son and some other kids enjoyed playing with this, where you had to balance discs on a spinning circle. If you balance it correctly, the disc spins round with the circle – for a while!

My son played with this for a long time and it seems nice. You use the shapes to make shadows of the right size and shape, tilting to make e.g. the circle shape cast an oval pattern.

He enjoyed making a Penrose tiling on a table they have at MathsCity too, and I was pleased to see the ‘hat’ tile was already featured in a small exhibit.

He tells me he enjoyed the Pythagorean Theorem demonstrations.

This one was very nice and clear – the red and yellow squares are blue on the back, so you swap the area between the blue hypotenuse and the red and yellow sides.

The balance scale was cute – you weigh the objects on the sides to illustrate the theorem. I wonder how much these help understanding the theorem for people who don’t already get it, but it was certainly a memorable illustration.

He spent a long time rolling back and forth on these!

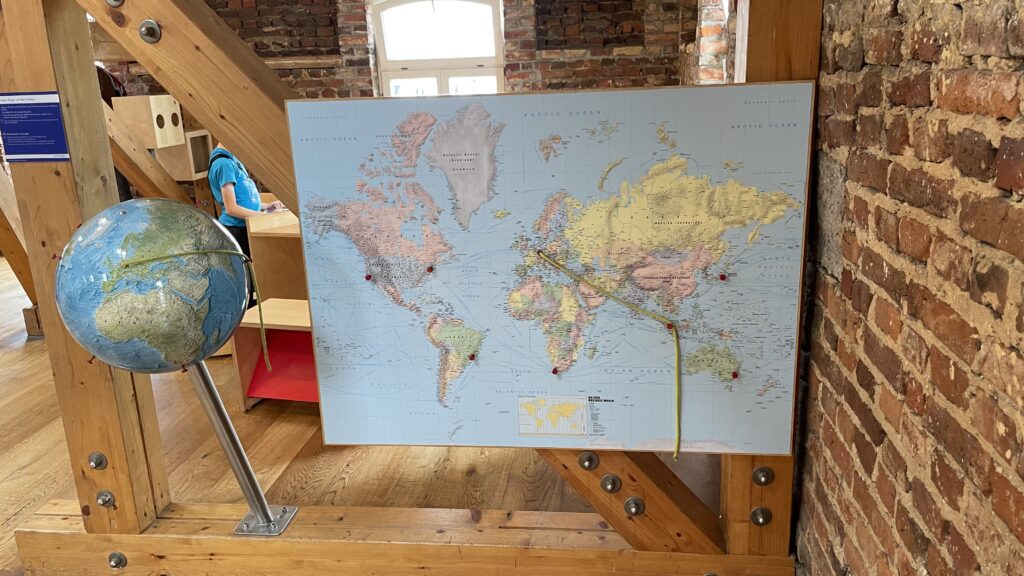
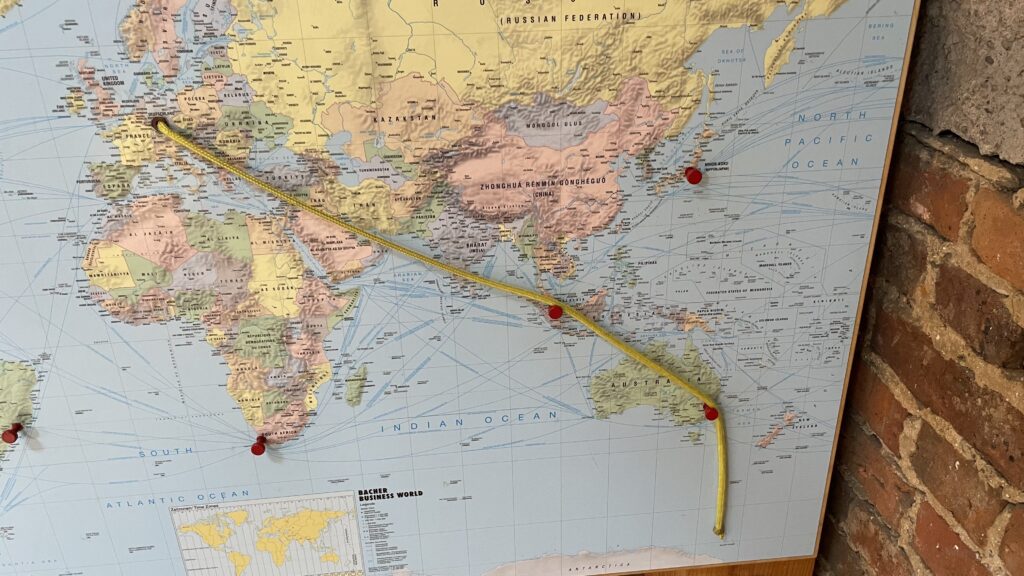
We both enjoyed this, which demonstrates the difference between a globe and a projection by seeing which countries a line passes through on its way between two points and noticing these are different on the globe from the map.

We also both enjoyed the catenary curve, which you build laying down then tilt upright using a hinged board.

This was a really nice demo of the Mobius strip and he enjoyed driving the cars round it – starting on ‘opposite’ sides and then they crash.

He liked the ‘one in a million’ demo and it seemed nice. You spin a cylinder of a million little balls, one of which is a different colour. Apparently people tend to think of ‘needle in a haystack’ and guess the odd one can’t be found, but actually the one different-coloured ball stands out very clearly.

We enjoyed producing the stages of the Koch snowflake – starting with the red triangle pins, then moving the string to first the yellow, then the blue pins to illustrate the fractal forming.

There was loads more we enjoyed. I’ve tried to focus on things we hadn’t seen in Leeds that he particularly enjoyed playing with on the day, and that I had pictures of.