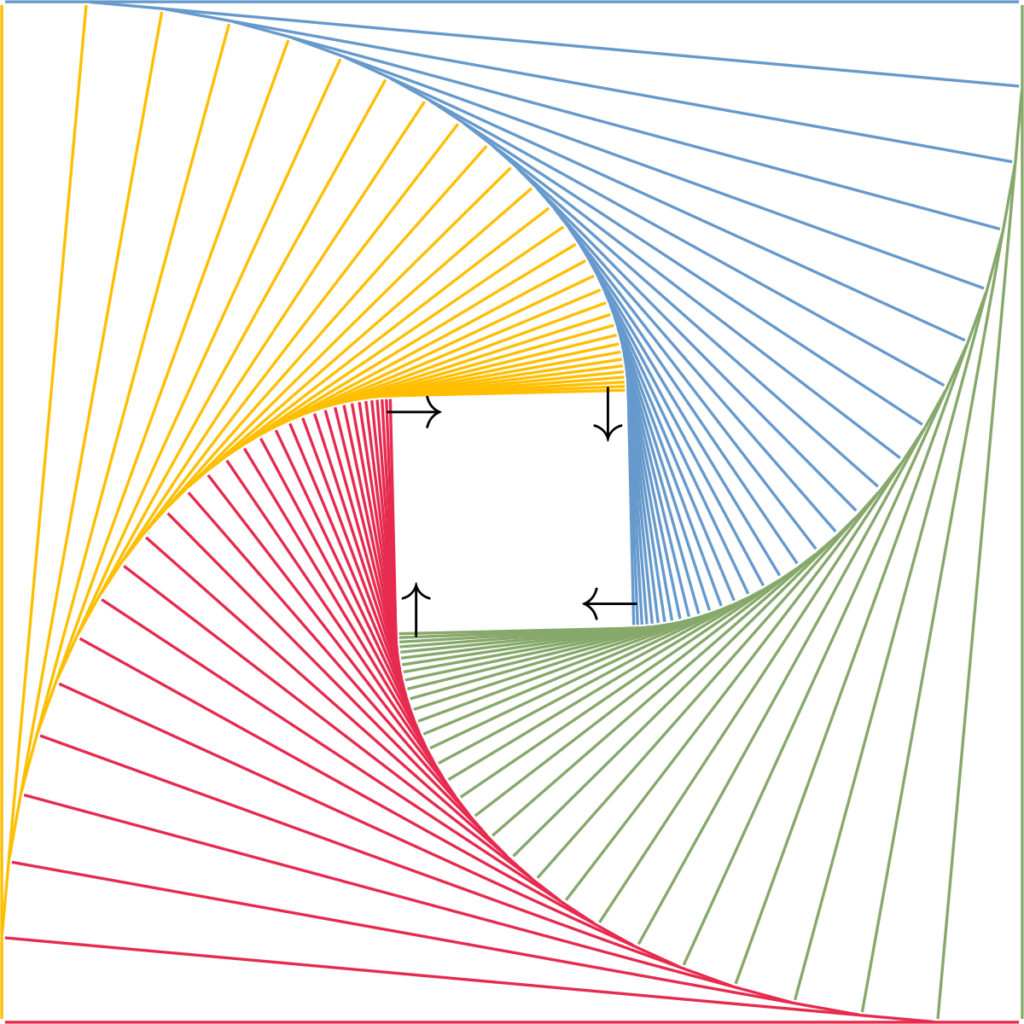
Reminder: I’m occasionally working to (sort of) recreate Martin Gardner’s cover images from Scientific American, the so-called Gardner’s Dozen.
This time I’m looking at the cover image from the July 1965 issue, accompanying the column on ‘op art’ (which became chapter 24 in Martin Gardner’s Sixth Book of Mathematical Diversions from Scientific American).

The image relates to a puzzle that was included in an earlier column, one of the ‘Nine More Problems’ in chapter 12 of his first collection Mathematical Puzzles and Diversions. It goes like this:
Four beetles — A, B, C, and D — occupy the corners of a square 10 inches along a side. A and C are male, B and C are female. Simultaneously A crawls directly towards B, B towards C, C towards D, and D towards A. If all four beetles crawl at the same constant rate, they will describe four congruent logarithmic spirals which meet at the centre of the square. How far does each beetle travel before they meet? The problem can be solved without calculus.
I tried to code this image in the spirit of the original puzzle. So I’m thinking of it as a series of time steps in which each bug moves a distance towards its partner.
In TikZ, first I set up some variables to hold coordinates.
\newcommand{\coorda}{10}
\newcommand{\coordw}{0}
\newcommand{\coordb}{0}
\newcommand{\coordx}{0}
\newcommand{\coordc}{0}
\newcommand{\coordy}{10}
\newcommand{\coordd}{10}
\newcommand{\coordz}{10}Then I made a loop in TikZ using
\foreach \i in {0,...,30}{
}Inside this loop, I drew the four points using \node (A) at (\coorda,\coordw) {}; and similar, and drew lines between these nodes like \draw (A) -- (B);
Now inside the loop I need to move each bug, so they get closer as the loop iterates. Considering A at \((a,w)\) and B at \((b,x)\), it looks like this:
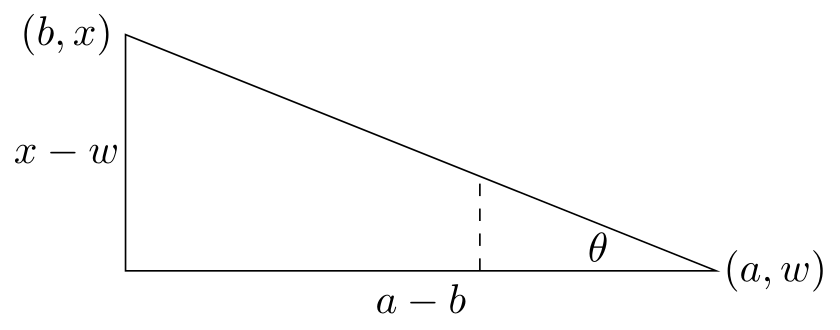
The angle \(\theta\) is given by
\[ \theta = \tan^{-1} \left( \frac{x-w}{a-b} \right)\text{.} \]
I want to move the bug at A to the top of the dashed line. Say this is a distance \(d\) along the hypotenuse. Then the horizontal distance moved is given by \( d \cos \theta \) and the vertical distance by \( d \sin \theta \).
In the TikZ loop, I did this using \pgfmathsetmacro{variable}{calculation}, which performs PGF calculations and stores them in the variable named.
\pgfmathsetmacro{\angle}{atan((\coordx-\coordw)/(\coorda-\coordb))}
\pgfmathsetmacro{\hdist}{\rate*cos(\angle)}
\pgfmathsetmacro{\vdist}{\rate*sin(\angle)}The variable \rate is the distance each bug moves, and it shrinks as we loop because I noticed in the original the lines start further apart and get closer. I found the numbers by trial and error.
Finally I adjust each bug by these distances and then store the values in the coordinate variables. I had to store each in a dummy variable using \pgfmathsetmacro and then store these in the coordinate variables using \global\let after I worked out that \pgfmathsetmacro only stores the value for the current iteration of the loop and they need transferring to a global variable to be used further.
At the end I drew four arrows instead of four bugs, since I’m in it for the maths rather than the art!
Here’s the result: