Here’s the fifth match in Round 1 of The Big Internet Math-Off. Today, we’re pitting Matt Peperell against Fran Watson.
Take a look at both pitches, vote for the bit of maths that made you do the loudest “Aha!”, and if you know any more cool facts about either of the topics presented here, please write a comment below!
Matt Peperell – An unexpected use for the Fibonacci sequence
A reminder
The Fibonacci sequence is a sequence in which each term is the sum of the previous two, starting with 0 and 1 (less commonly 1 and 1, or 1 and 2). The sequence in its most common form begins as follows: \(0, 1, 1, 2, 3, 5, 8, 13, 21, 34,55, 89, \ldots\)
Adjacent pairs of this sequence taken as a quotient converge alternately higher and lower on a value known as the golden ratio, written as \(\phi\). Despite the approximations being rational, the converged-on value is, in fact, irrational and is approximately equal to 1.618033988749.
A slightly different value
An exact quotient which has a similar value to this is \(\frac{25146}{15625} = 1.609344\). This ratio precisely links SI kilometres to miles, with the mile being the longer unit.
Approximating the conversion between miles and kilometres
More common applications and occurrences of the Fibonacci sequence involve pentagons, snail shells and sunflower seeds. But outside of nature, using two adjacent terms of the Fibonacci sequence allows us to convert between miles and kilometres with a theoretical error of \(\frac{\phi-1.609344}{1.609344} \approx 0.53997\%\), though the actual error value will vary and depend on the integer rounding. Some examples:
| Miles | Approximation in km | Actual value in km | Error |
|---|---|---|---|
| 5 | 8 | 8.04672 | -0.581% |
| 13 | 21 | 20.921472 | +0.375% |
What about values not found in the Fibonacci sequence?
We can perform simple calculations on these values. E.g. multiplication by 10 is trivial:
| Miles | Approximation in km | Actual value in km | Error |
|---|---|---|---|
| 50 | 80 | 80.4672 | -0.581% |
| 80 | 130 | 128.74752 | +0.973% |
We can also decompose values into partitions, convert those individually, and then perform addition:
| Miles | Approximation in km | Actual value in km | Error |
|---|---|---|---|
| 58 = 50 + 8 | 80 + 13 = 93 | 88.51392 | -0.366% |
| 173 = 80 + 80 + 13 | 130 + 130 + 21 = 281 | 278.416512 | +0.928% |
Note that the errors can compound or counteract, depending on whether the terms used are in odd or even positions in the series.
Converting other units
We do not need a conversion factor directly similar to the golden ratio; we can operate at powers of 10. This gives us access to some other possible conversions:
- Cubic inches to cubic centimetres
- 1 cubic inch = 16.387064 cm3
- Magnitude: \(\times 10\)
- Approximate error 1.262…%
- Worked example:
- 10 cubic inches
- 10 = 5 + 5 → 8 + 8 = 16
- \(16 \times 10 = 160\) cm3 (real value is 163.87064)
- Milligrams to grains
- 1 mg = 0.01543236 grains
- Magnitude: \(\div 100\)
- Approximate error 4.847…%
- Worked example:
- 8 mg
- 8 → 13
- \(13 \div 100 = 0.13\) grains (real value is 0.1234589)
- Minutes to hours
- 1 minute = 0.0166…hrs
- Magnitude: \(\div 100\)
- Approximate error 2.918…%
- Worked example: 130 mins,
- Worked example:
- 130 mins
- \(130 = 13 \times 10 \to 21 \times 10 = 210\),
- \(210 \div 100 = 2.10\) hrs (real value is 2.166…)
As before, conversion with this technique gives an approximation: further mistakes creep in due to integer rounding.
Can you come up with any other unit conversions? Remember to take care with the magnitude.
 Matt Peperell is a London-based recreational mathematician living a double-life as a software developer. Outside of work and when not doing maths he likes bellringing and playing board games. You can follow him on Mathstodon.
Matt Peperell is a London-based recreational mathematician living a double-life as a software developer. Outside of work and when not doing maths he likes bellringing and playing board games. You can follow him on Mathstodon.
Fran Watson – Winning at playing rather than playing to win
As an enthusiastic player of games, I particularly love those that have an obvious puzzle or mathsy element to them, but also tend to look for the maths wherever possible and “Kingdomino” has been subjected to this a lot since lockdown when it was a staunch favourite.

Even without any more information about the game, think about the questions you already want to ask about this picture: Is it significant that some of the tiles are upside down? Why is the tile in the middle different? What do the colours mean? Where do you start? How do you win? The list goes on! Learning games involves lots of question posing (in my experience at least) and even if you try to remember the rules from the start, sometimes you need to be immersed, before being ready to ask the questions needed to make sense of it for yourself – a lot like learning mathematics.
If you don’t already know this game I’ll give a brief outline to start with, but if you do, you might like to look at the picture above, think about what order the pieces could have been played in and then skip ahead to paragraph 4. The picture above is my board at the end of a game. Everyone playing (usually 2-4 people) is aiming to build their own 5×5 board in front of them, comprising a starting tile (the square tile with the dashed outline) and 12 other domino-type pieces which are laid, one per round, in any orientation according to the following rules. Tiles must either be placed next to one of the four sides of the starting square or have at least one end matched in colour/land type to a tile that’s already been laid, and once they are placed tiles can’t be moved (unless you’re feeling kind to your opponents!) Players are aiming to score as highly as possible at the end of the game by multiplying the number of sections of any contiguous area of the same colour/land type by the total number of crowns in that area. (Alongside the land types of forest, pasture, swamp and sea, I’ve always thought of the yellow squares as desert, but realise now on closer scrutiny of the pictures that they’re wheat fields!)
So my board would score 24 points, as the starting tile isn’t worth any points and neither are the three other areas that don’t have any crowns in them. And there the game usually ends…
… only now is when it can get interesting if you dismantle your board and using the same tiles each, allow rebuilding, abiding by the same rules, but with the difference that as you know all your tiles in advance, you might make new choices about how to assemble them. The starting tile doesn’t have to end up in the middle, as shown in a few examples below (ignore the numbers on the back of the dominoes, they aren’t to do with scoring, only to do with the order of play when selecting them as your next choice).
In fact there are some positions of the starting square that might mean you can’t complete the 5×5 array, leaving some of your tiles unplayed so that there are “holes” in your board (this is a whole other investigative track to happily womble down, particularly for people who’ve never met tiling puzzles before). You might find that you’re doing a whole load of visualising, experimenting, comparing and figuring out, without even realising you’re working mathematical muscles!

So now you’ve a second total score, which could be the maximum possible for the tiles you have (I think mine would be 30 in the picture above) and might mean that your position in the leaderboard is different to the end of the original game. Finding the difference between your two totals is another nice metric for “most improved” player (6 extra points between my first and second goes here) and sometimes helping your opponents make even higher scores with their tiles (upon invitation of course) is oddly satisfying, and I say this as someone who is usually fiercely competitive!
Other questions have arisen whilst playing about what tiles could come up/are available in the game as a whole (a little like wanting to know the letter frequencies of Scrabble tiles to see if you’ve already had all the Js) but the only information provided in the rules booklet is this:
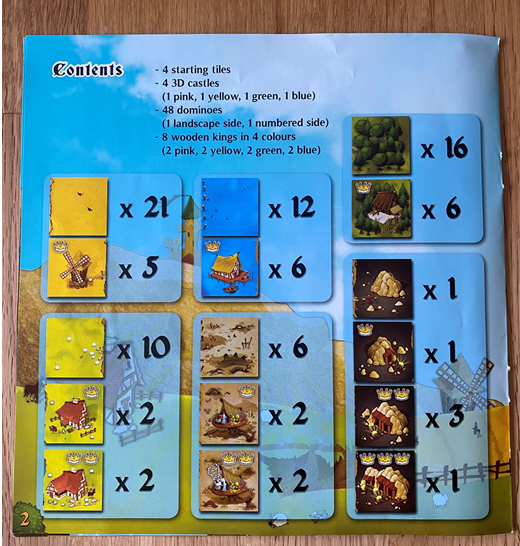
Although you’re given some information, you’re not told what the make-up of the 48 individual dominoes are, so unless your memory helps you out from previous games, each tile turned over is a surprise at the beginning of a turn. The exception to this in our house, is tile number 25. This was excitedly chewed by a friend’s dog in his eagerness to play! So if all this has whetted your appetite for more maths in the form of “Kingdomino” (in which I had also over looked the Kingdom reference, until recently – I should clearly pay more attention to the instructions and less to the winning it would seem) I will finish by bequeathing you the dubious insider advantage of knowing what tile number 25 looks like after being mangled by Ozzy!


 Fran Watson is a teacher and communicator of mathematics originally hailing from Cornwall but now living in Cambridgeshire (by way of Cardiff in between – locations today brought to you by the letter C!) She loves puzzles, origami, games and musical theatre and will endeavour to weave these passions into her pitches.
Fran Watson is a teacher and communicator of mathematics originally hailing from Cornwall but now living in Cambridgeshire (by way of Cardiff in between – locations today brought to you by the letter C!) She loves puzzles, origami, games and musical theatre and will endeavour to weave these passions into her pitches.
So, which bit of maths has tickled your fancy the most? Vote now!
Match 5: Matt Peperell vs Fran Watson
- Fran with Kingdomino scores
- (51%, 76 Votes)
- Matt with Fibonacci conversions
- (49%, 74 Votes)
Total Voters: 150
This poll is closed.
The poll closes at 08:00 BST tomorrow. Whoever wins the most votes will get the chance to tell us about more fun maths in the quarter-final.
Come back tomorrow for our sixth match in round 1, pitting Ayliean against K.P. Hart, or check out the announcement post for your follow-along wall chart!



I love the idea of using the Fibonacci series to do unit conversions. Or Lucas numbers, too.