The Aperiodical 

You're reading: Posts By David Benjamin

Pythagoras and his theorem

By David Benjamin. Posted October 14, 2023

In this guest post, David Benjamin shares a cornucopia of concepts and stories relating to Pythagoras and his famous theorem.

I admit to mild irritation when I’m told that Pythagoras’ theorem is $a^2+b^2=c^2$. The theorem is based on area – in particular, that of squares. There are many proofs of the theorem and in this post we present a miscellany of Pythagorean Theorem curiosities, including some of my favourite proofs, the theorem’s links to algebra, geometry and number theory, an assassination of a president of the USA, an alleged murder in Greece, an infinite spiral of surds, Gauss and coordinate geometry – plus another connection between Pascal and Fibonacci.

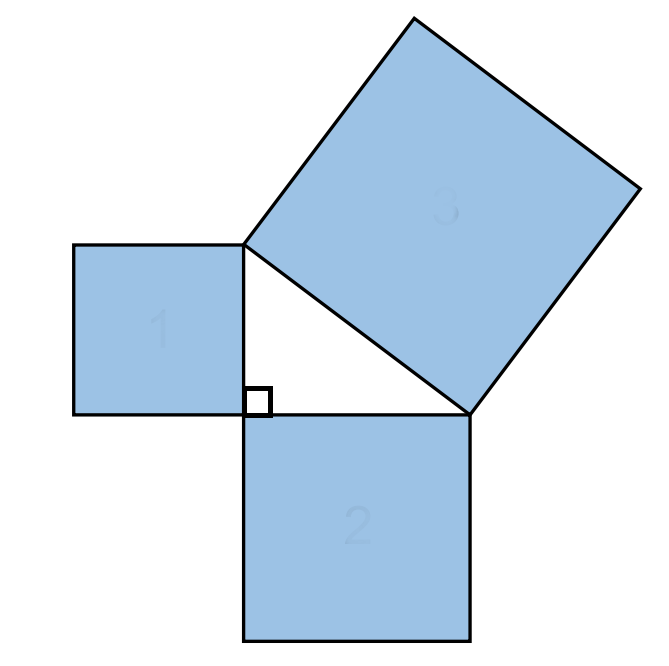
The theorem



A square is added to each side of a right-angled triangle as shown in the above image. The sum of the the areas of the two smaller squares is equal to the area of the largest square. If the hypotenuse of the triangle has a length of $c$ and the other two sides are of length $a$ and $b$ then $a^2+b^2=c^2$

When the length of each side of the triangle is a positive integer, the three numbers make a Pythagorean triple. $(3, 4, 5)$ is the smallest triple with $3^2+4^2=5^2$. The Chinese text Chou Pei Suan Ching – original title Zhoubi – (周髀算经), (The Arithmetical Classic of the Gnomon and the Circular Paths of Heaven) gives this visual proof for the $(3, 4, 5)$ triple.



$(3, 4, 5)$ is a primitive triple since $3, 4$ and $5$ are coprime – their only common divisor is $1$. $(n\times3, n\times4, n\times5), n = 2, 3, 4,…$ are part of the same ‘family’ and clearly not primitive triples. Another primitive triple is $(5, 12, 13)$ and an ordered sequence of hypotenuses for such triples are listed here. In the sequence I was surprised to see $185$ appearing twice. In fact there are exactly four distinct triples with hypotenuse $185$. With the aid of a spreadsheet, I was able to find them: $(57, 176, 185), (60, 175, 185),(104, 153, 185)$ and $(111, 148, 185)$

Generating Pythagorean triples

The sequence $\frac{1}{1},\frac{3}{2},\frac{7}{5},\frac{17}{12},\frac{41}{29},\frac{99}{70},\frac{239}{169},\frac{577}{408},\frac{1393}{985},…$ produces a Pythagorean triple from every other term beginning with $\frac{7}{5}$:

$\frac{7}{5}=\frac{3+4}{5} \rightarrow 3^2 + 4^2 = 5^2$

$\frac{41}{29}=\frac{20+21}{29} \rightarrow 20^2 + 21^2 = 29^2$

$\frac{239}{169}=\frac{119+120}{169} \rightarrow 119^2 + 120^2 = 169^2$

$\frac{1393}{985}=\frac{696+697}{985} \rightarrow 696^2 + 697^2 = 985^2$

…

As an added bonus, the decimal equivalent of each term of the sequence converges to $\sqrt2$, in a similar way the Fibonacci sequence converges to the golden ratio $\psi=\frac{1+\sqrt5}{2}$

Another method to find Pythagorean triples uses consecutive even numbers and the sum of their reciprocals as shown below.

Choose any pair of consecutive even numbers:

$8$ and $10$ $\rightarrow \frac{1}{8} + \frac{1}{10} = \frac{9}{40} \rightarrow 9^2 + 40^2 = 1681 = 41^2$

$12$ and $14$ $\rightarrow \frac{1}{12} + \frac{1}{14} = \frac{13}{84} \rightarrow 13^2 + 84^2 = 7225 = 85^2$

$20$ and $22$ $\rightarrow \frac{1}{20} + \frac{1}{22} = \frac{21}{220} \rightarrow 21^2 + 220^2 = 48841 = 221^2$

Euclid of Alexandria (325BC – 265BC) was a Greek mathematician who wrote a treatise, The Elements – a collection of 13 books. Books 1 to 6 are on plane geometry and books 7 to 9 on number theory. Euclid created a formula for generating Pythagorean triples from any pair of positive integers $m$ and $n$, where $m>n$:

($m^2-n^2, 2mn, m^2+n^2$) is the triple.

If $m=7$ and $n=3$, the triple is ($40, 42, 58$) $\rightarrow 40^2 + 42^2 = 3364 = 58^2$

If $m=89$ and $n=11$, the triple is ($7800, 1958, 8042$) $\rightarrow 7800^2 + 1958^2 = 64673764 = 8042^2$

A lovely link between Pascal, Fibonacci, Euclid and Pythagoras comes via any four consecutive Fibonacci numbers

$F_{1}$	$F_{2}$	$F_{3}$	$F_{4}$	$F_{5}$	$F_{6}$	$F_{7}$	$F_{8}$	$F_{9}$	$F_{10}$
$1$	$1$	$2$	$3$	$5$	$8$	$13$	$21$	$34$	$55$

Using $3, 5, 8, 13$

• Multiply the first and the last numbers $\rightarrow 3 \times{13}=39$
• Multiply then double the middle two numbers $\rightarrow 5 \times{8}\times{2}=80$
• Sum the squares of the middle two numbers $\rightarrow 5^{2}+8^{2}=89$
• The Pythagorean triple is $(39, 80, 89) \rightarrow 39^{2}+80^{2}=7921=89^{2}$

$F_{1}$ to $F_{4}$ gives the primitive triple $(3, 4, 5)$

$F_{2}$ to $F_{5}$ gives the primitive triple $(5, 12, 13)$

$F_{3}$ to $F_{6}$ gives the triple $(16, 30, 34)$

$F_{7}$ to $F_{10}$ gives the primitive triple $(715, 1428, 1597)$

In addition, for any set of four consecutive Fibonacci numbers, $F_{7}$ to $F_{10}$ for example, the following connection is true

$7+10=17$ and the $17^{th}$ Fibonacci number is $1597$, the third member of the triple, the hypotenuse of the triangle!

Amazingly, if we use $m$ and $n$ as consecutive Fibonacci numbers when using Euclid’s method, then the last number of the triple is again a Fibonacci number

$m$	$n$	Triple	Fibonacci number
$2$	$1$	$(3, 4, 5)$	$5^{th}$
$3$	$2$	$(5, 12, 13)$	$7^{th}$
$5$	$3$	$(16, 30, 34)$	$9^{th}$
$8$	$5$	$(39, 80, 89)$	$11^{th}$
$13$	$8$	$(105, 208, 233)$	$13^{th}$

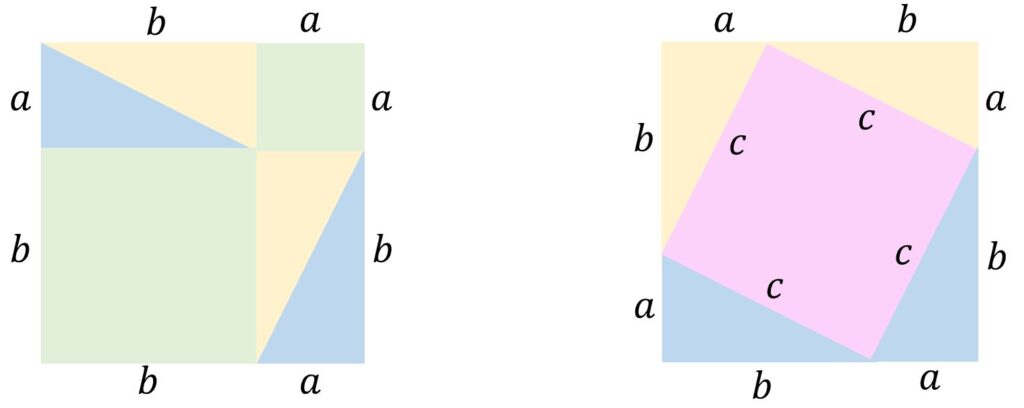
A visual proof of the theorem

I first came across a visual proof of Pythagoras’ theorem for all right-angled triangles in Roger B. Nelsen’s wonderful book Proofs Without Words, Exercises in Visual Thinking. Nelsen noted the proof (author unknown, circa B.C. 200?) is adapted from the Chou Pei Suan Ching. The two images below combine to show the proof:



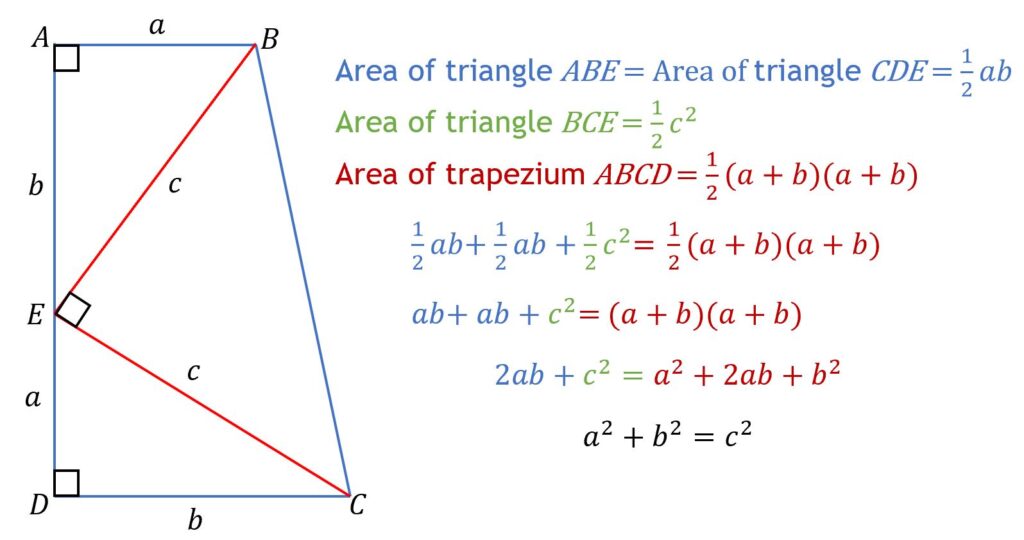
A proof by trapezium area and an untimely painful death

James Garfield (November 19, 1831 – September 19, 1881) was elected as the United States’ 20th President in 1880. He was assassinated after just 200 days in office after being shot on July 2, 1881, in a Washington railroad station. Garfield remained mortally wounded in the White House for many weeks where Alexander Graham Bell, inventor of the telephone, attempted to locate the bullet with an induction-balance electrical device which he had designed. Bell and physicians were unsuccessful in their attempts and Garfield died from an infection and an internal haemorrhage on September 19, 1881.



In 1876, Garfield had an elegant proof of Pythagoras’ theorem published. The proof makes use of the formulae for the areas of a triangle and a trapezium. The proof is demonstrated in the image below



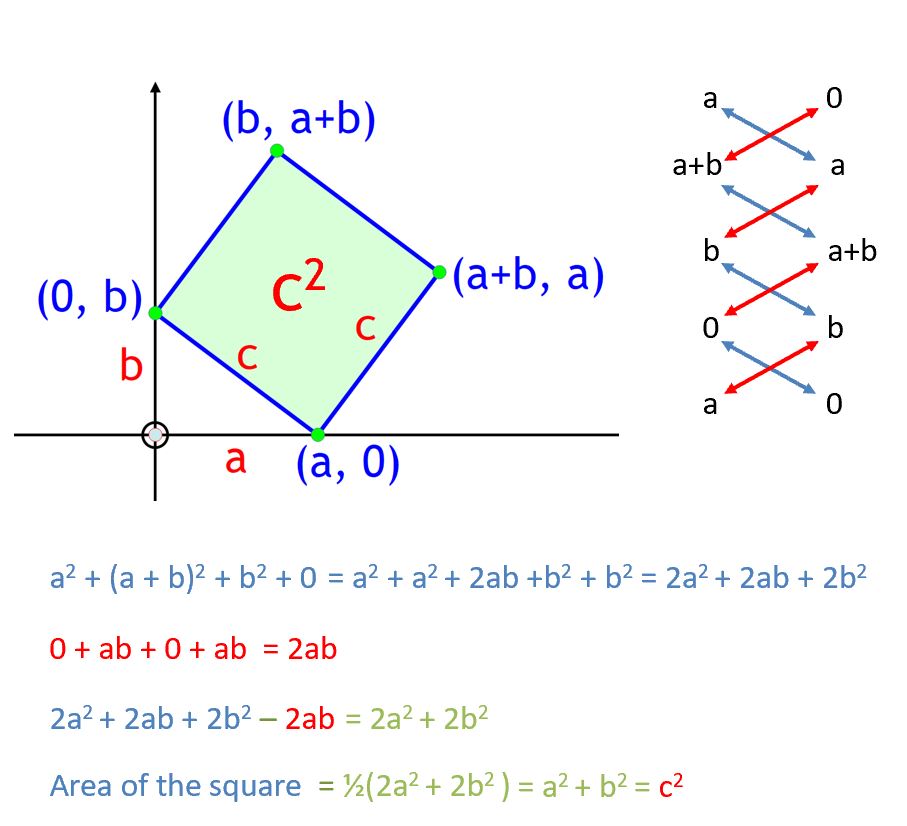
A proof using the Shoelace formula

The brilliant German mathematician Johann Carl Friedrich Gauss (30 April 1777 – 23 February 1855) developed a formula to calculate the area of a polygon if every vertex of the polygon lies on a known Cartesian coordinate. The formula is widely known as the Shoelace formula and makes use of the calculation to find the determinant of a 2 by 2 matrix.



John Molokach observed that the Pythagorean theorem follows from Gauss’ Shoelace Formula, as shown below



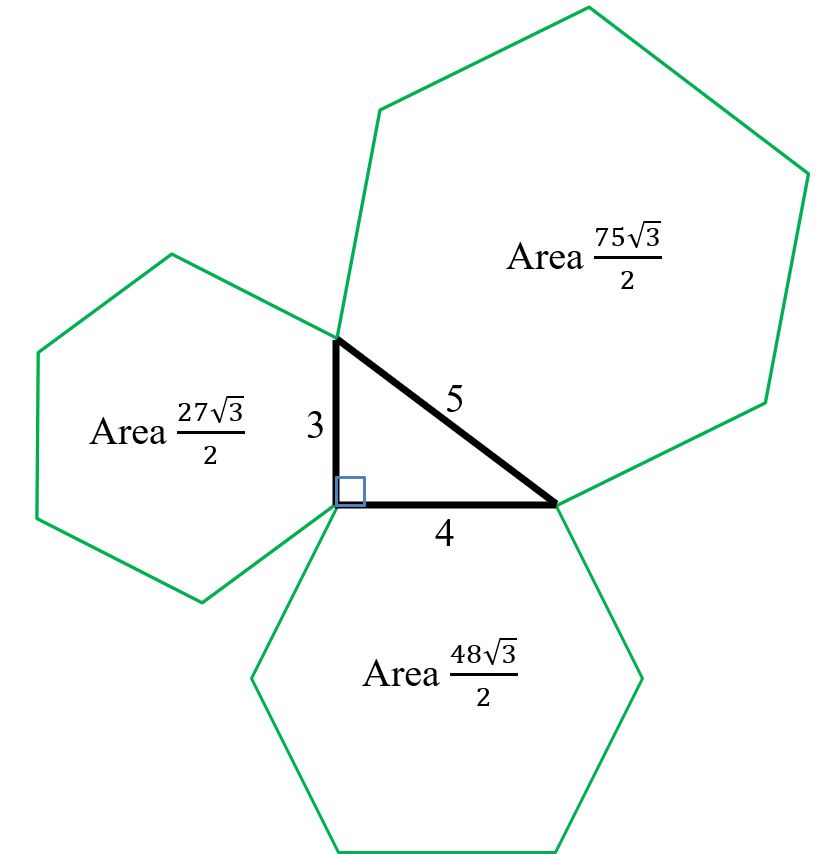
It’s not just squares

If the same regular $n$-gon, $n$ = 3, 4, 5,.. is drawn on each side of a right-angled triangle, then the sum of the areas of the two smaller $n$–gons equals the area of the $n$–gon on the hypotenuse. Semicircles also produce the same result. As $n\rightarrow \infty$, a regular $n$-gon approaches a circle and so circles, where the sides of the triangle act as tangents to the circles can be said to satisfy Pythagoras’ theorem. The same result can be obtained by rotating the semicircles through $180^ \circ$ and adding matching semicircles.



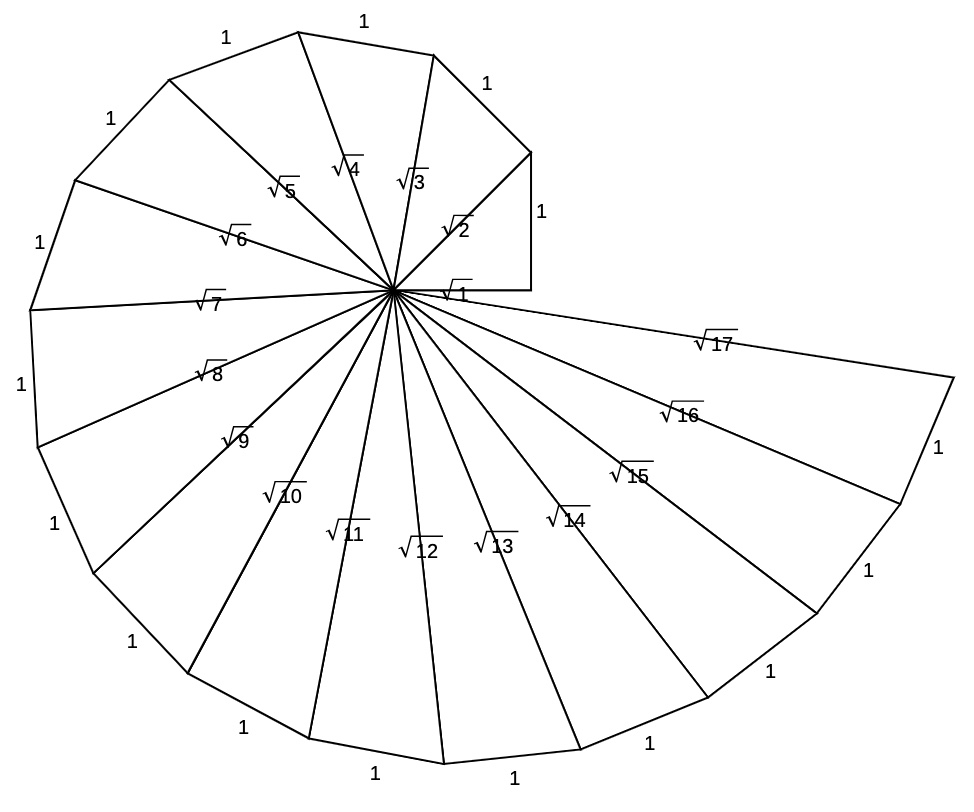
The spiral of Theodorus of Cyrene

When $n$ is not a square number, $\sqrt{n}$ is called a surd

Pythagoras and his followers, the Pythagoreans, believed that the universe can be explained by whole numbers and the ratio of whole numbers. Their moto – “All is number” – was carved above the entrance of their meeting place. However, a spanner was thrown in the works when Hippasus of Metapontum, one of the Pythagoreans suggested that $\sqrt2$, the length of the hypotenuse of the right-angled triangle with sides $1, 1$ and $\sqrt2$, could not be written as the ratio of two whole numbers. Such numbers are now called irrational and it was approximately 200 years before Euclid of Alexandria proved $\sqrt2$ was irrational. The Pythagoreans were sworn to secrecy and one legend suggests that Hippasus was thrown off a boat and drowned for revealing his discovery to non-Pythagoreans. Then again, some believe Hippasus drowned because he revealed how to construct a dodecahedron inside a sphere. The ($1, 1$,$\sqrt2$) triangle is the start of the spiral of Theodorus. Further right-angled triangles, each containing a side of length $1$ unit, are added sequentially to produce the sequence $\sqrt2, \sqrt3, \sqrt4, \sqrt5,…$. The sequence is the length of each new hypotenuse, as shown in the diagram below. Theodorus probably stopped at $\sqrt17$ as it the length of the hypotenuse of the triangle before the triangles begin to overlap. The spiral can be expanded here.



Further reading

• The Euclidean distance formula and it’s extension to higher dimensions
• The Pythagoreans and music – Donald Duck in Mathmagic Land
• Biography search of included mathematicians
• 2 High School Students Prove Pythagorean Theorem – proof awaiting verification
• Pythagorean trigonometric identities
• The latest Mersenne prime and a Pythagorean triple
• Related themes – Legendre’s three-square theorem and Fermat’s theorem on sums of two squares

Alternative methods of arithmetic

By David Benjamin. Posted June 15, 2023

This is a guest post by David Benjamin, who’s previously written several other guest posts on various topics.

It’s unavoidable that part of doing mathematics will always involve arithmetic: the simple calculations, additions and multiplications that so much else is built on. But the beauty of mathematics is that even these basic operations can be performed in a multitude of interesting ways.

Recurring decimals and 1/7

By David Benjamin. Posted January 9, 2023

This is a guest post by David Benjamin.

Rational numbers, when written in decimal, either have a terminating string of digits, like $\frac{3}{8}=0.375$, or produce an infinite repeating string: one well-known example is $\frac{1}{7}=0.142857142857142857…$, and for a full list of reciprocals and their decimal strings, the Aperiodical’s own Christian Lawson-Perfect has built a website which generates a full list.

I’ve collected some interesting observations about the patterns generated by the cycles of recurring decimals, and in particular several relating to $\frac{1}{7}$.

Sequences in the classroom

By David Benjamin. Posted August 8, 2022

Guest author David Benjamin shares some of his favourite ways to use sequences in a teaching context.

As a maths teacher, I’ve found that sequences are a great way to engage and inspire mathematical reasoning. I thought I’d share some examples of sequences, and sequence-related activities, I’ve used with success in the past.

John Conway and his fruitful fractions

By David Benjamin. Posted March 25, 2022

Following on from the series of ‘Pascal’s Triangle and its Secrets‘ posts, guest author David Benjamin shares another delightful piece of mathematics – this time relating to prime numbers.

At the time of writing the largest known prime number has $24862048$ digits. The number of digits does not reflect the true size of this prime but if we were to type it out at Times New Roman font size 12, it would reach approximately $51.5$ km, or about $32$ miles. Astonishing!

Patrick Laroche from Ocala, Florida discovered this Mersenne prime on December 7, 2018. I was surprised to discover that it’s exponent $82589933$ is the length of the hypotenuse of a primitive Pythagorean triple where $82589933^{2} = 30120165^{2} + 76901708^{2}$ as indeed are 8 of the exponents of those currently ranked from 1 to 10.

The Greek mathematician Euclid of Alexandria ($\sim$325 BC-265 BC) was arguably the first to prove that there are an infinite number of primes – and since then, people have been searching for new ones. Some do it for kudos, for the prize money, to test the power of computers and the need to find more of the large primes used to help protect the massive amount of data which is being moved around the internet.

Mersenne primes, named after the French monk Marin Mersenne, are of the form $2^{p} -1$, where the exponent $p$ is also prime. Mersenne primes are easier to test for primality, which is one reason we find so many large ones (all but one of the top ten known primes are Mersenne). When Mersenne primes are converted to binary they become a string of $1$s, which makes them suitable for computer algorithms and an excellent starting point for any search.



Since generally testing numbers for primality is slow, some have tried to find methods to produce primes using a formula. Euler’s quadratic polynomial $n^2+n+41$ produces this set of $40$ primes for $n = 0$ to $39$. When $n=40$, the polynomial produces the square number $1681$. Other prime-generating polynomials are listed in this Wolfram Mathworld entry.

The French mathematician Lejeune Dirichlet proved that the linear polynomial $a+nb$ will produce an infinite set of primes if $a$ and $b$ are coprime for $n=0,1,2,3,4,…$. Then again, it also produces an infinite number of composite numbers! However, this gem: $224584605939537911 + 1813569659748930n$ produces 27 consecutive primes for $n=0$ to $n=26$ – and of course, all the primes are in arithmetic progression.

14 fruitful fractions

The primes are unpredictable, and become less common as they get larger. Consequently there is no formula that will generate all the prime numbers. However, there is a finite sequence of fractions, that – given an infinite amount of time – would generate all the primes, and in sequential order.

They are the fruitful fractions, created by the brilliant Liverpool-born mathematician, John Horton Conway (1937–2020) who, until his untimely death from complications related to COVID-19, was the John von Neumann Emeritus Professor in Applied and Computational Mathematics at Princeton University, New Jersey, USA.



The fruitful fractions are

$\frac{17}{91}$

$\frac{78}{85}$

$\frac{19}{51}$

$\frac{23}{38}$

$\frac{29}{33}$

$\frac{77}{29}$

$\frac{95}{23}$

$\frac{77}{19}$

$\frac{1}{17}$

$\frac{11}{13}$

$\frac{13}{11}$

$\frac{15}{44}$

$\frac{15}{2}$

$\frac{55}{1}$

A

B

C

D

E

F

G

H

I

J

K

L

M

N

The first time I encountered this set of fractions was in the wonderful book, The Book of Numbers, by Conway and Guy. I was so intrigued as to how Conway came up with his idea, I emailed him to ask. I was delighted to receive an outline of an explanation and even a second set of fractions, neither of which I can now find – it was 1996 and pre-cloud storage! But no worries… Conway explains everything in this lecture, which also demonstrates his passion for mathematics and his ability to express his ideas in a relaxed and humorous way, even when he searches for an error in his proof on 26 minutes. The lecture also includes an introduction to Conway’s computer language, FRACTRAN, which includes the statement:

‘It should now be obvious to you that you can write a one line fraction program that does almost anything, or one and a half lines if you want to be precise‘.

Using the fractions to find prime numbers

Here’s how the fractions are used to generate primes.

• Start with the number $2$
• Multiply by each of the fourteen fractions until you find one for which the product is an integer
• Starting with this new integer, continue multiplying through the fractions until another integer is produced. (If this process reaches fraction $N=\frac{55}{1}$, the integer’s product with N is guaranteed to be another integer as N has a denominator of $1$; the process continues with this new integer being multiplied by fraction A)
• Continue multiplying through the set to create more integers
• When the integer is a power of $2$, its exponent will be a prime number.

The 19 steps needed to produce the first prime number are:

$2 \overset{ \times M}{\rightarrow} 15 \overset{ \times N}\rightarrow 825\overset{ \times E} \rightarrow 725 \overset{ \times F}\rightarrow 1925\overset{ \times K} \rightarrow 2275 \overset{ \times A}\rightarrow 425 \overset{ \times B}\rightarrow 390 \overset{ \times J}\rightarrow 330 \overset{ \times E}\rightarrow 290 \overset{ \times F}\rightarrow 770 \overset{ \times K}\rightarrow 910\overset{ \times A} \rightarrow 170\overset{ \times B} \rightarrow 156\overset{ \times J} \rightarrow 132\overset{ \times E} \rightarrow 116 \overset{ \times F}\rightarrow 308\overset{ \times K} \rightarrow 364\overset{ \times A} \rightarrow 68 \overset{ \times I}\rightarrow 4 \equiv2^{2}$

The number of steps needed to produce the first 7 primes are shown in the table below:

Prime	2	3	5	7	11	13	17
Steps	19	69	281	710	2375	3893	8102

And here is the start and end of the sequence of fractions used to produce the next prime number from $2^{2}$:

$4 \overset{ \times M}{\rightarrow} 30 \overset{ \times M}\rightarrow 225\overset{ \times N} \rightarrow 12375 \overset{ \times E}\rightarrow 10875 \rightarrow \cdots \rightarrow 232 \overset{ \times F}{\rightarrow} 616 \overset{ \times K}\rightarrow 728\overset{ \times A} \rightarrow 136 \overset{ \times I}\rightarrow 8\equiv2^{3}$

The steps needed for the first 34 primes are given as OEIS A007547 and the first 8102 products in the B-list for A007542.

The successive primes are produced almost like magic – but the number of multiplications needed to produce each new prime becomes larger and larger, and so the method, though wonderfully inventive, is not at all efficient.

Edit: Since this article was first published, the exponent $82589933$ of the Laroche prime has been accepted as the next term in the sequence http://oeis.org/A112634

Further Reading on John Conway

• Listen to this Numberphile interview with Conway on how he invented the Game of Life
• Play the Game of Life
• Aperiodical posts about John Conway
• Conway’s publications on Scholia
• Conway and knots: ‘I proved this when I was at high school in England’
• Graduate Student Solves Decades-Old Conway Knot Problem, in Quanta

Probability, statistics and Pascal’s other contributions

By David Benjamin. Posted March 4, 2022

This is the final part in the Pascal pentalogy, a series of guest posts by David Benjamin exploring the secrets of Pascal’s Triangle.

Probability and combinations

In Part 1 of this series we stated that Pascal is credited with being the founder of probability theory – but credit also needs to be given to other mathematicians, in particular the Italian polymath Girolamo Cardano.

The connection between probability and the numbers in Pascal’s triangle can be shown by looking at the outcomes when one or more coins are tossed. The table below, from row two, lists the outcomes for one, two and three unbiased coins.

				$1$
			$1$ H		$1$ T
		$1$ HH		$2$ HT, TH		$1$ TT
	$1$ HHH		$3$ HHT, HTH, THH		$3$ HTT, THT, TTH		$1$ TTT
$1$		$4$		$6$		$4$		$1$

For four coins there is $1$ outcome for four heads, $4$ outcomes for three heads and one tail, $6$ outcomes for two heads and two tails, $4$ outcomes for one head and three tails and one outcome for $4$ tails.

Row four shows us that when three unbiased coins are tossed, the probability they will land showing two heads and one tail in any order is $\frac{3}{1+3+3+1}=\frac{3}{8}$.

As the sum of the $n^{th}$ row is $2^{n}$, the number of possible outcomes for four coins is $2^4=16$, $32$ for five coins, $64$ for six coins, …

Quincunx

A Quincunx, or Galton Board, is named after the English explorer and anthropologist Francis Galton (1822-1911) – although this name is now less popular, because of Galton’s views on eugenics and racist attitudes.



The board is a triangular array of pegs. Balls are dropped onto the top peg and then bounce their way down to the bottom where they are collected in containers. Each time a ball hits one of the pegs, it bounces either left or right with an equal probability of $\frac{1}{2}$ and the balls collect in the containers to form the classic bell-shaped curve of the normal distribution.



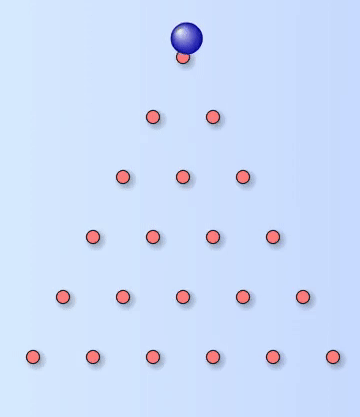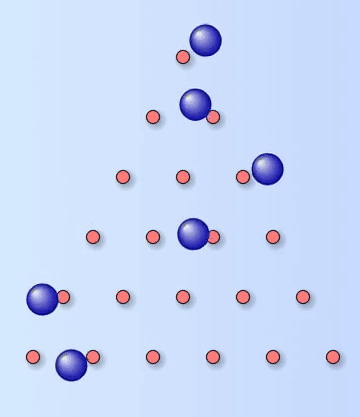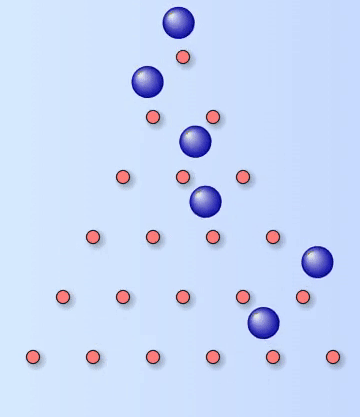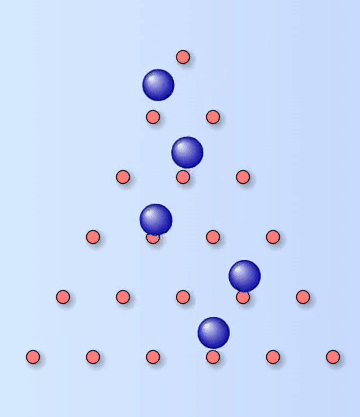
The Quincunx is like Pascal’s triangle with pegs instead of numbers. The number on each peg represents the number of different paths a ball can take to reach that peg. If there are $10$ rows and the last row contains the containers, then the probability of landing in the third container from the right can be calculated by using the formula for the Binomial distribution.

The probability of landing in the third bin from the right is $120\times(\frac{1}{2})^3\times(\frac{1}{2})^7=\frac{15}{128}=0.1171875$, where $120$ is the number of different paths to that bin.

Statistics and permutations

The link between statistics and the triangle can be demonstrated using combinations. Consider these 5 mathematicians Euler, Pascal, Ramanujan, Hilbert and Conway and the possible teams for a three-legged race.

There are $10$ different teams of $3$:

EPR      EPH     EPC     ERH    ERC   EHC    PRH    PRC    PHC    RHC

The formula to calculate the number of combinations is $_n{C}_r =\frac{n!}{r!(n-r)!}$ where $n$ represents the total we are choosing from, $r$ the number in the team and

\[ n!=n\times(n-1)\times(n-2)\times(n-3)\times…\times1\]

In our example $n=5$, $r=3$ and $\frac{5!}{3!(5-3)!}=\frac{120}{6\times2}=10$

$_n{C}_r$ can be used to calculate the rows of Pascal’s triangle as shown below for row $6$, where in the calculation of $_5{C}_0$, $0!=1$

$_5{C}_0$	$_5{C}_1$	$_5{C}_2$	$_5{C}_3$	$_5{C}_4$	$_5{C}_5$
$1$	$5$	$10$	$10$	$5$	$1$

The animation film Of Dice and Men by John Weldon is a lovely way to introduce students to probability and statistics.

Pascal the polymath: mathematics, inventor, science and religion

Pascal’s father was a tax collector and in 1642 Blaise invented a mechanical calculator to assist his father. It was called the Pascaline and had a wheel with eight movable parts for dialing. Each part corresponded to a particular digit in a number. Numbers could be added by turning the wheels located along the bottom of the machine. Subtraction was carried out by exploiting a method called nines’ complement representation, the use of which allows subtraction to be reduced to addition. Each digit in the answer was displayed in a separate window. The workings of the Pascaline are demonstrated here.





The Musée des Arts et Métiers in Paris has one of the original Pascalines. The invention was not a commercial success – it was very expensive and often only purchased as a novelty rather than for use. Essentially, it was an adding machine. Subtraction was turned into a form of addition, as was multiplication. Division was done by repeated subtraction. Nines’ complement representation is still used in modern digital computers by a similar technique called ones’ complement which is used to represent negative numbers and hence perform subtraction in the same way as addition. Pascal did not discover this method but his calculator is the earliest known device to employ it. He continued to make improvements to his design until 1652.

Conic sections – normally just called conics – are obtained when a mathematical cone is sliced by a plane. Depending on the angle of the slice, the intersections create a circle, an ellipse, a parabola and a hyperbola. Conics have many applications including the wheel of course, ophthalmic, parabolic mirrors and reflectors, telescopes, searchlights and projectile motion.

Pascal wrote a short treatise, Essai pour les coniques (Essay on Conics) when only 16. In it he included what is known as Pascal’s Theorem which states that if a hexagon is inscribed in a conic section then the three intersection points of opposite sides lie on a straight line – the Pascal line. The theorem [also referred to as Pascal’s Hexagrammum Mysticum Theorem] was his first important mathematical discovery and a breakthrough in the field of projective geometry.



In 1647 Pascal expanded on the work of the Italian physicist Evangelista Torricelli, the inventor of the barometer by writing Experiences nouvelles touchant le vide (New experiments with the vacuum) in which Pascal gave detailed rules to describe to what degree various liquids could be supported by air pressure. In 1971 the SI unit for pressure [equal to one newton per square metre] was named the pascal.



Also in 1647 he discovered Pascal’s Law of hydrostatics allowing for the development of the hydraulic press. Pascal himself used the principle to invent the syringe.



Pascal wrote an extremely influential theological work which was unfinished at the time of his death. It was posthumously called Pensées (Thoughts) and contained a detailed and coherent examination and defence of the Christian faith.



In 1655 Pascal was trying to invent a perpetual motion machine, a machine that continues to operate without drawing energy from an external source. The laws of physics now say this is impossible. Naturally he failed but he ended up inventing a basic roulette wheel, now upgraded and used in casinos as a game of chance.

The Swiss computer scientist Niklaus Emil Wirth, born in 1934, named one of his programming languages Pascal in honour of Blaise. Wirth along with Helmut Weber also designed the programming language named after another mathematician, Euler. [Recommended read: Euler: The Master of Us All ]

Pascal died in extreme pain at the young age of 39. He had a malignant growth in his stomach which had spread to his brain. Like many others, such as Évariste Galois and Franz Schubert, we are left wondering what else Pascal could have achieved had he lived longer. His work with Fermat into the calculus of probabilities helped the German mathematician Gottfried Leibniz [1646-1716] develop the infinitesimal calculus. Pascal is buried in the Saint-Étienne-du-Mont church in Paris and his death mask is held at the J. Paul Getty museum in Los Angeles, California.



Numbers and number patterns in Pascal’s triangle

By David Benjamin. Posted February 4, 2022

This is the fourth in a series of guest posts by David Benjamin, exploring the secrets of Pascal’s Triangle.

Triangles and fractals

If we highlight the multiples of any of the Natural numbers $\geq 2$ in Pascal’s triangle then they create a pattern of inverted triangles.



The images above are evocative of the Sierpinski sieve (also known as the Sierpinski gasket or Sierpinski’s triangle), a fractal described in 1915 by the Polish mathematician Waclaw Sierpiński (1882-1969).





Fractals are beautiful geometric shapes. Small, even down to (theoretically) infinitesimal areas of a fractal are identical to the entire shape. The Koch snowflake, generated geometrically by successive iterations on an equilateral triangle, is an example of a fractal. Julia sets and Mandelbrot sets are examples of fractals generated using recursion on complex functions. Many examples of fractals appear in nature, and the Polish-born French-American polymath Benoit Mandelbrot (1924-2010) suggested that fully developed turbulent flows are fractals.

It is a lovely surprise to discover that a simple fractal can be found inside Pascal’s triangle. It is achieved by considering all the numbers in the triangle modulo 2 – equivalent to colouring in only the multiples of 2, as in the first diagram at the top of the post. In this version, every odd number becomes $1$ and every even number becomes $0$, and by considering sufficiently many lines of the triangle, the Sierpinski pattern emerges.





Number patterns in the triangle

If we consider the first 32 rows of the mod$(2)$ version of the triangle as binary numbers: $1, 11, 101, 1111, 10001,…$ and convert them into decimal numbers, we obtain the sequence:

\[1, 3, 5, 15, 17, 51, 85, 255, 257, 771, 1285, 3855, 4369, 13107, 21845, 65535, 65537, \]

\[196611, 327685, 983055, 1114129, 3342387, 5570645, 16711935, 16843009, \]

\[50529027, 84215045, 252645135, 286331153, 858993459, 1431655765, 4294967295\]

Interestingly, all members of this sequence are factors of the final term, $4294967295 = 2^{32} – 1$. Since this is one less than a power of two, it’s a Mersenne number. Why the first $31$ terms are all factors of the 32nd term is difficult to summarise here but there is a thread on StackExchange discussing what happens to the pattern after the $32nd$ term.

$4294967295$ has prime factorisation $3 \times 5 \times 17 \times 257 \times 65537$. These five prime factors are Fermat numbers – numbers of the form $2^{2^{n}}+1$ – in this case with $n = 0, 1, 2, 3$ and $4$. As of the time of writing these are the only known Fermat numbers which are also prime.

These patterns in the rows of the triangle are intriguing, and my own efforts to understand them have uncovered a few other interesting discoveries – notably, that while the 32nd term is not divisible by the 33rd, the 34th term is exactly 3 times the 33rd. The pairs of terms after that seem to alternate, as they do from the start of the sequence, between a non-integer ratio and a ratio of exactly 3, which I conjecture is a pattern that will continue.

Two welcome appearances

$e$ and $\pi$ are two of the most used transcendental numbers. The Swiss mathematician Leonhard Euler (1707-1783) connected them with the most beautiful equation, called Euler’s identity:

\[e^{i\pi}+1=0\]

There are many approximations connecting $e$, $\pi$ and other irrational numbers to be found here.

In 2012 Harlan J. Brothers proved that

\[\displaystyle\lim_{n\to \infty} \frac{\ \displaystyle\frac{s_{n+1}}{s_n}\ }{\displaystyle\frac{s_n}{s_{n-1}}}=e\]

where $s_n$  is the product of the numbers on row $n$ of Pascal’s triangle. The proof can be found on Cut the Knot, part of the wonderful website of Dr Ron Knott.

In 2007 Jonas Castillo Toloza discovered a connection between $\pi$ and the reciprocals of the triangular numbers (which can be found on one of the diagonals of Pascal’s triangle) by proving

\[\pi= 2 + \frac{1}{1} + \frac{1}{3} – \frac{1}{6} – \frac{1}{10} + \frac{1}{15} + \frac{1}{21} – \frac{1}{28} – \frac{1}{36} + \frac{1}{45} + \frac{1}{55} – \ldots\]

Three proofs are given on Cut the Knot.

Harmony in the triangle

The infinite sum of the reciprocals of the Natural numbers is called the harmonic series, $H_n$, where

$H_n = \frac{1}{1} + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \frac{1}{5} + \frac{1}{6} + \frac{1}{7} + \frac{1}{8} \ldots$

The series is divergent, but it crawls its way towards infinity, and takes $15092688622113788323693563264538101449859497$ terms just to pass a total of $100$.

The harmonic series can be used to create a version of Pascal’s triangle – the series itself is placed along the two leading diagonals, and the entries are then related by each being the difference of the fraction to its left, and the one diagonally above it and to its left. For example, $\frac{1}{30} = \frac{1}{5}-\frac{1}{6}$.



Dividing the first term in the $n^{th}$ row by every other term in that row creates the $n^{th}$ row of Pascal’s triangle. The table below shows the calculations for the $5^{th}$ row:

$\frac{1}{5}$	$\frac{1}{20}$	$\frac{1}{30}$	$\frac{1}{20}$	$\frac{1}{5}$
$\frac{1}{5}\div \frac{1}{5} =1$	$\frac{1}{5}\div \frac{1}{20} =4$	$\frac{1}{5}\div \frac{1}{30} =6$	$\frac{1}{5}\div \frac{1}{20} =4$	$\frac{1}{5}\div \frac{1}{5} =1$

In our next post, we’ll talk about probability and statistics in Pascal’s triangle, and consider some of Pascal’s other contributions.