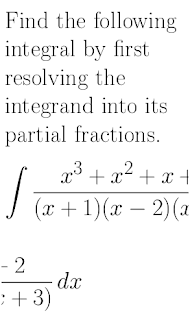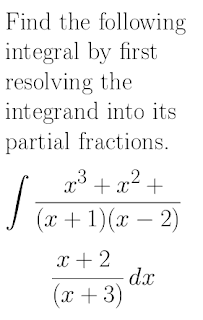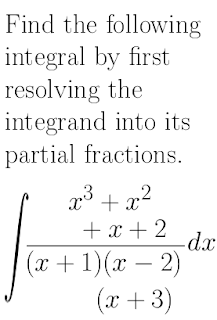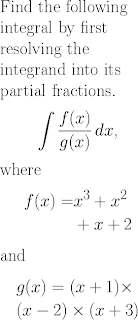In December I organised a series of online public maths talks called What Can Mathematicians Do?
The recordings of the talks are now online, free for anyone to watch. You could go to the official page I put up on Newcastle University’s website, or you could just watch them here!
I’ve put together a series of online public maths presentations, to take place in the last couple of weeks of term before Christmas.
This came about after a few people on the Talking Maths in Public WhatsApp group complained that we can hardly ever take up requests for a speaker to deliver a fun maths talk due to our disabilities, usually because of the difficulty of travelling to and from an event. I quipped that we should set up a series of talks for non-commutative mathematicians, and then I was told that the department’s EDI committee had a load of money sitting unused in its budget. So I decided to use some of it!
MathJax, the web library that provides LaTeX-quality mathematical typesetting, has received a a new set of tools to improve accessibility of mathematical notation. The new MathJax Accessibility Extensions add on-the-fly speech rendering of notation, and a tool to explore expressions through intelligent collapsing and expanding of sub-expressions.
My collaborators at The Aperiodical, Katie Steckles and Christian Perfect, have launched a new mathematics magazine podcast called All Squared. In the first episode, number one1, Katie and Christian speak to Edmund Harriss about speaking mathematics out loud.
Towards the end of the conversation, they speak a little about some of the ambiguity in spoken mathematics and how this might affect blind mathematicians. Particularly, they speak about timing and ambiguity, and Christian gives the example (where the comma is a pause): ‘x plus, y squared’ and ‘x plus y, squared’. The placement of the pause changes the meaning of the formula substantially.
A few minutes ago the conference ‘Supporting Disabled Students in STEM‘ began at the Royal Society. This is the spring conference of the STEM Disability Committee (an alphabet soup collaboration between IOP, RAEng, RSC, SoB, CaSE and RS). I am not attending this, though I was asked a couple of weeks ago for two examples for a session at this.
For the first example, I was asked for a formula that would be a bit difficult to read aloud. The aim is not for an unrealistic expression or to trick the audience, but just for something that might cause ambiguity and mean that the reader would stop and think. Here is the equation (apologies for the use of images throughout):
The exercise, later today, will use two volunteers. One reads the formula aloud and the other, with back turned to the screen, will write it down. Try it now with the person on the next desk or in the next office. I’ll wait.
This is the Taylor expansion of ln(x) around x=2. It is an example from a problem sheet in my first year methods course a few weeks ago, so it isn’t unrealistic. I chose it because there are two particular points of possible ambiguity. The first is in “minus one to the power i plus one”. The second is to have the top be “all over n times two to the n”. Is the “one” included in the power? Is the “two to the n” included in the bottom half of the fraction? There are also some conventions for non-mathematicians in the room to take note of, such as the pronunciation of “ln” and the way we read out “sum over i from one to infinity”. All of this means that to be read well requires a thoughtful, mathematically-trained reader.
If the person reading the equation in the session today does it badly then the other volunteer will write the equation wrong and the point will be made. If they do it well, it will be interesting to hear them speak to the group about what choices they made when reading the equation to reduce the ambiguity.
The second example was a piece of mathematics that would need to be broken over two lines when enlarged, and that would be difficult to do so. Here the grey is supposed to indicate the edge of the page. Have a think about it: how would you break this equation to fit on the page (you can’t make it smaller!)?
Again this is an example from class, a partial fractions question. A naive solution might be to simply cut the equation at the page edge. You can hopefully see in the following image that this is unacceptable, in particular because the 2 on the next line looks like -2.
A more intelligent cut might be to take whole terms onto the next line. However, this may cause confusion because it looks like the (x+3) is part of a separate fraction. Is it one fraction plus another? One fraction multiplied by another? This perhaps isn’t unusable, provided you explain to the reader what you have done, but you are presenting the reader (your student?) with non-standard and, strictly speaking, incorrect mathematical notation. If part of being a mathematician is learning to speak and write mathematics so that other mathematicians can understand you, you are doing damage here.
Here I try to keep the two halves of the fraction together by including in-line cuts. This is still weird, particularly the bottom half, but I could imagine writing something like this by hand (perhaps with a multiplication symbol on the bottom cut) so maybe it’s okay.
Finally, here is what I think I would do. The result is mathematically correct and using fairly standard notation (we wouldn’t ordinarily use multiplication symbols in g(x) but this is unusual rather than strictly wrong).
This is hopefully a good solution, but there are still two problems. Interpreting the two functions back into the partial fractions form is an extra cognitive load for this student (not related to the intended learning outcomes of the question), and producing this formatting is a giant amount of extra work compared with the original code. Here is the original LaTeX:
Find the following integral by first resolving the integrand into its partial fractions.
$$ \int \frac{x^3+x^2+x+2}{(x+1)(x-2)(x+3)} \, dx $$
And here is the adapted LaTeX code that produced the last version.
Find the following integral by first resolving the integrand into its partial fractions.
$$ \int \frac{f(x)}{g(x)} \, dx \text{,}$$
where
\begin{align*}
f(x)= \, &x^3+x^2\\
&+x+2
\end{align*}
and
\begin{align*}
&g(x)=(x+1)\times\\
&(x-2)\times(x+3)
\end{align*}
The person who adapts this page must be properly trained in mathematics, so they don’t introduce errors into the notation and adapt it sensibly, and in this case they must know LaTeX to be able to write the code. This is an unusual set of skills for a generalist disability support professional, and the maths department might be unable to commit personnel to do this. Sometimes the problems are that mathematics notation is difficult to adapt, and sometimes they are to do with the practicalities of who is able to do the work.
I will leave you with this quote from Christian in the podcast.
It is very rare for someone who is blind to get through to becoming a research mathematician, isn’t it? … So is that because the culture isn’t accommodating or because maths is a thing that really is much easier to understand visually?
Something for you to think about. Listen to the podcast to hear what Edmund thinks.
If you are interested in these issues, Emma Cliffe is running a workshop ‘Mathematical Study Without Pen and Paper: Experiences, Impacts and Options‘ for the Higher Education Academy on 20th March 2013 at Manchester Metropolitan University. Attendance is highly recommended.
1. It is an open question, as far as I know, whether the second episode will be number two or number four.