In going through a hard drive I came across some playing around I did a couple of years ago with Truchet tilings which I thought I would share with you here.
I came across Truchet tilings in a talk a couple of years ago by Cameron Browne to the London Knowledge Lab‘s Maths-Art Seminar Series. (Sébastien Truchet is the first person I have thought would be in but found not to be in The MacTutor History of Mathematics archive).
To cut an interesting story short, Truchet tiles come in two forms which can be represented as:

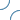
These are then combined to form interesting curves, thus:

You can colour these tiles, making four visually different tiles:




So the pattern becomes like:

Or the inverse.
So. if you think about it, the two types of tile can be used to represent two points – for example binary data – using the two symbols  and
and 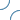 .
.
At the time I was playing around with Braille notations for mathematics. Braille characters are made up of 3 rows of 2 cells each (or, in some advanced forms, 4 rows of 2 cells). Cells contain raised dots or don’t and the pattern is used to feel which character is which. Representing raised dots as black dots and, then the Braille character for, say, “m” is:

If we take this as a pattern of 1s (raised dots) and 0s (absence of dots) then this is:
0 0
1 0
If we take one Truchet symbol to be a raised dot and the other to be the absence of such a dot then we can represent a pattern of dots as a Truchet tiling. So, for example take  to be a raised dot and
to be a raised dot and 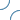 to be the absence. Then a British Braille “m” is:
to be the absence. Then a British Braille “m” is:

Or a coloured version:

Okay, so then I looked for something suitable to encode this way. I chose Euler’s identity. Taking  to be a raised dot and
to be a raised dot and 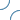 to be the absence I encoded the identity using the BAUK Braille Mathematics Notation and coloured this using one colouring or the other, chosen aesthetically. This gives (click to enlarge):
to be the absence I encoded the identity using the BAUK Braille Mathematics Notation and coloured this using one colouring or the other, chosen aesthetically. This gives (click to enlarge):

Finally, I gave this a bit of a colouring and eroded the shapes in a way I thought looked appealing. Please click on the following to enlarge:

Really this is all very contrived but I quite like it. Of course, there is something contrary to intentions about generating a visually appealing image from a tactile representation. I think the pattern is attractive and the hidden meaning, and particularly of such a beautiful formula, I think adds something to the effect.