This month’s MathsJam was well attended – we matched last month’s turnout of 11, albeit one of that number was in the form of Ed Bradshaw, the organiser of the Washington DC MathsJam. For Ed, it was 4pm and he was in his office, using Google Plus for a live video connection to a MathsJam halfway around the world. The video connection worked fine, although in a noisy pub we struggled to hear what Ed was saying on my laptop’s tiny speakers, so for some of the evening we used headphones and took it in turns to be in conversation with Ed.

We started off with some ‘ice-breaker’ puzzles I picked up from a recent schools event. What is the smallest number which has each of the numbers 1 to 9 as a factor? We stepped up to the next puzzle: find a 4-digit number (not zeroes) such that if you multiply it by 4, the result is the same 4 digits in the reverse order. ‘ABCD’ x 4 = ‘DCBA’. We held the sheet up to the webcam, and there was some confusion as to whether the webcam is mirroring the image left-to-right, as it shows my output to Ed mirrored so that the motion of my face on the screen matches the motion of my actual face; Ed confirms he’s seeing it the right way round – although, he adds, for this puzzle it doesn’t matter!

Richard, an undergraduate from the university, is here for the first time. He poses the following: if you list successive powers of 11, you get 1, 11, 121, 1331, 14641, and then at 11^5 the pattern of Pascal’s triangle breaks and you get 161051. His question is: why does this happen, and also, why do you get lines of Pascal’s triangle for the first five lines?

Ed described this puzzle: a car is 90 feet away from a brick wall, and it is travelling towards the wall at 90 feet/second, and its speed is changing so that the speed in ft/s is always equal to the distance away from the wall – when it is 80ft from the wall, it will be travelling at 80 ft/s and so on. How long does it take before the car is 1 foot from the wall? It’s quite a nice question, and the answer is almost kind of what you’d expect it to be. A couple of us managed to get it by calculation before the night was over!

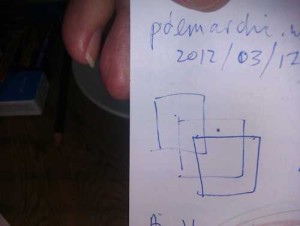
Colin has brought some puzzles by Lewis Carroll; firstly, can you draw this figure (pictured, right) without retracing a line or taking your pen off the paper? It’s not hugely difficult, but Colin points out he uses it with school students, whom he asks to write a program in Logo to draw the shape – a more worthy task! Another one from Lewis Caroll: An oblong garden, half a yard longer than it is wide, consists entirely of a gravel-walk, spirally arranged, a yard wide and 3630 yards long. Find the dimensions of the garden.

Another quick icebreaker – a tetrahedron has one face painted green. You have pots of blue, red and yellow paint for the other faces. Each face has to be painted exactly one of these colours. How many different designs are possible?

Ben, who is an accomplished bridge player, poses the following question. A deck of cards is dealt into four bridge hands, and you receive one hand of 13 cards. Your task now is to sort the hand into four (or fewer, if they are not all present) suits, and then within each suit to have the cards ordered by rank (either direction is fine, as long as it’s consistent among the suits). What is the maximum minimum number of moves of cards you’ll need to achieve this? In other words, what’s the most moves you’ll need to do it in the most efficient way? One move is counted as taking a card out and placing it elsewhere in the hand. Various approaches are discussed; Ben suggests the maximin might be around 7, although he found a hand last night which needed 8. Paul writes down a hand consisting of the 13 cards of one suit in the order 5 4 3 8 7 9 J 10 9 A K Q 2, which can’t be done in fewer than 9 moves.

On Twitter, we learn Glasgow are discussing the Princess in a Castle puzzle, which prompts us to describe it to those present (and Ed) who haven’t heard it before. A nice writeup of the discussion of the puzzle at Newcastle MathsJam can be found here. Glasgow have found a solution for four rooms in a line which means a find can be guaranteed in five nights. Peter Rowlett suggests there’s a quicker solution, much to their frustration.

Steve, who has been sitting across the room all night, finally joins us and describes a fantastic fact he recently learned about a problem involving two billiard balls of masses M and m, which are on a frictionless plane leading up to a wall. Assuming all collisions are elastic, and the ball with mass M is travelling towards first the other ball and then the wall with constant velocity v, how many collisions will there be? Obviously, if M=m then the balls will collide, the ball with mass m will bounce off the wall, and rebound into the first ball, which will then move off forever, resulting in a total of three collisions. However, if M is considerably larger than m, an interesting pattern appears. If M = 10^{2mk}, the number of collisions will be exactly the first k (+1?) digits of pi, ignoring the decimal point. Everyone is suitably amazed. The fact is more nicely explained here, here and in this paper.

How many zeroes are on the end of 100! (100 factorial)?

Lewis Caroll again: a captive Queen and her son and daughter were shut up in the top room of a very high tower. Outside their window was a pulley with a rope over it, and baskets of equal weight were fastened to each end of the rope. They managed to escape with the help of this and a weight they found in the room, quite safely. It’d have been dangerous for anyone to come down if their weight differed more than 15lbs from the weight of the contents of the other basket, for they would fall too quickly. The Queen weighed 195lbs, the prince 105lbs and the princess 90lbs. The weight was 75lbs. How did they escape?

Two travellers spend from 3pm til 9pm in walking along a level road, up a hill, and back home again. Their pace on the level is 4mph, uphill 3mph and downhill 6mph. Find the distance walked and, within ½hr, the time of reaching the top of the hill.

The definition of Evil and Odious numbers is briefly discussed, and more detail can be found here.

At the end of the evening, again inspired by the puzzles discussed this evening, Andrew produced a lovely comic featuring the queen and her children trapped in a tetrahedral tower, whose sides are painted different colours, and while the prince confirms the room he’s looking in doesn’t contain the princess, the Queen has to hoist her daughter, while sorting cards into the right order in as few moves as possible, out of the way of a car approaching the wall of the tower at 90 ft/s.