Guest post by Andrew, of Manchester MathsJam. Andrew can be found on Twitter as @andrew_taylor and blogs occasionally about maths, among other things, at andrewt.net.
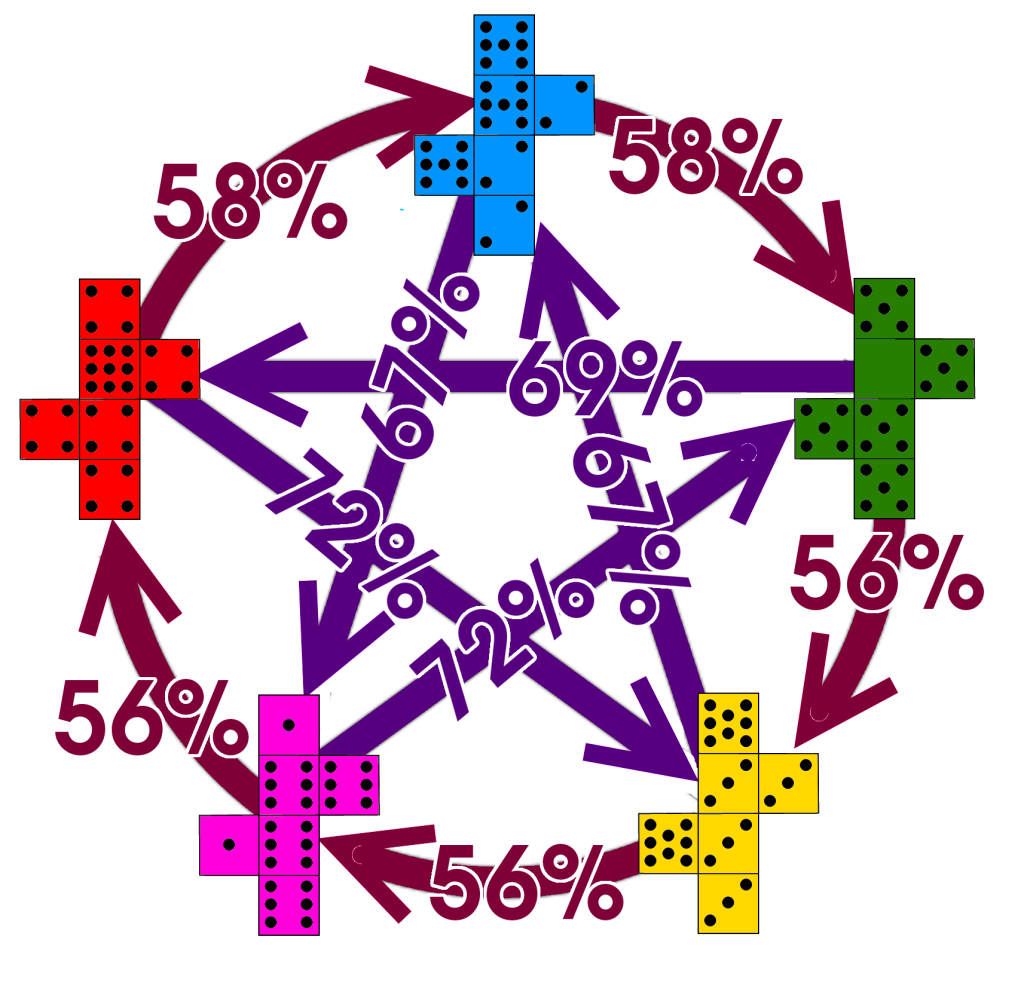
“Grime Dice” are a set of five coloured dice with unusual combinations of numbers on them. The red die, for example, has five fours and a nine. The blue one has three twos and three sevens, so it loses to the red die about 58% of the time. The green die has five fives and a zero, and will lose to the blue one in 58% of rolls. What makes them interesting is that the green die will beat the red one in 69% of rolls. These three dice behave rather like rock-paper-scissors — in mathematical terms, they are ‘non-transitive’. The full set of Grime Dice also has a purple and a yellow die, so a better analogy would be rock-paper-scissors-lizard-Spock.
You might ask which is the best Grime die, and the obvious solution is just to roll all five dice at once, a hundred times, and see which one wins the most times. This is why you should never believe something simply because it is obvious.
In the 18th Century, the Marquis de Condorcet quite reasonably suggested that if ever there is a single candidate in a general election who would beat each of the other candidates in a head-to-head ballot, that candidate should be declared the winner. While it’s hard to see how there could ever not be such a candidate, we can construct an electorate that think this way using Grime Dice.
There are 6⁵ = 7,776 possible ways that five dice can land and each of these ways represents a voter. The dice represent ratings of candidates. So this voter:
…rates Labour 9/10, the Conservatives 7/10, the Greens 5/10, the Lib Dems 3/10, and UKIP only 1/10. If you do simply roll all five dice against each other, the blue and yellow dice will each win about 28% of the rolls, and we’ll end up with a Liberal-Conservative coalition — even though you can see from the first diagram that a majority of voters would rather have Labour than either. But if Labour were elected, a majority would prefer UKIP, to whom a majority would prefer either the Tories or the Lib Dems. This is Condorcet’s Paradox.
A problem with the “first past the post” system we just used is that even if there was a Condorcet winner, they might not win. Programmers call this a “naïve algorithm”, because it’s simple, easy to implement and sounds reasonable, but gives results that make no sense. It’s possible for the Condorcet loser to win a first-past-the-post election. You could end up with an MP who is less popular than any other person on the ballot.
That’s why, in May 2011, we had what the government flattered to call a “referendum” on the Alternative Vote, a rival system more usually known as “Instant Runoff” voting or “what they do on The X Factor”. After rolling the dice against each other a thousand or so times, we would eliminate the green one, which wins only 8% of the vote, and start again — the idea being that voters can both safely support the Greens and still have a say in the inevitable two-horse race that will actually decide the result. This time we eliminate UKIP, who have 19% (and predictably didn’t inherit any second-preference votes from Green supporters). Labour have inherited all the second-preferences so far, and as before the blue and yellow dice tie on 28%. The remaining 46% vote Labour, and whichever other die you eliminate, red wins.
AV isn’t actually that good either, though. You still won’t always get the Condorcet winner, and while you can’t get the Condorcet loser through the last round, there’s an even stranger quirk I’ll come to in a moment. So what else is there?
A simple one is “reverse plurality” — a sort of “last past the post” idea, where you vote for the worst candidate and the one with fewest votes wins. In our example, that’s Labour.
Then there’s a “reverse AV” system, called “Coombs’ Method” or “what they do on The Weakest Link”, where you eliminate the candidate with the most of these reverse votes, distribute their votes between the remaining candidates according to voter preference, and continue until there’s only one left. In our example, the blue and the purple dice each lose 28% of rolls. If we eliminate UKIP, the Tories crash out in the next round anyway and the Greens win — but if we eliminate the Tories, their inherited votes change things enough that UKIP go on to win the election outright. A right-wing Tory voter might be better off not voting, so that the Conservatives get knocked out and UKIP win rather than the Greens. This is the strange quirk I mentioned earlier: normal ‘forwards’ AV can punish you for voting in exactly the same way.
There’s a lot of other systems out there, but what I’m trying to put across here is: none of them are very good at all. Worse than that, Arrow’s Impossibility Theorem states that you can’t construct a system that isn’t at least slightly rubbish — essentially that there may not be a ‘best Grime die’, and while that might sound obvious we should by now know better than to accept it just on that basis.
All voting systems are compromises, but the best I’m aware of is the Schulze method. Also called “beatpath”, it has two of the five coolest names in electoral theory. (The other three are “Condorcet’s Paradox”, “Marquis de Condorcet” and “Arrow’s Impossibility Theorem”.) This method dispenses with rounds of voting, favourites and least favourites, and runs one big, exhaustive search over every voter’s full preference list.
A beatpath ballot paper looks exactly like an AV one, and you fill it in in the same way, numbering the candidates in order of preference. The first step in counting the votes is to use these ballots to build the diagram I posted at the start of this article. The next is to find the best path, along the victory arrows, from each die to each other die. A path is as strong as its weakest link, so the path from red to yellow is 72%, but there’s also a path from yellow to red (through blue, then green) whose strength is 58%, which would sound like a convincing argument that the yellow die is better than the red one if you have forgotten the whole point of non-transitive dice. When you’ve finished, and found the strongest path between each pair of dice, you get this:
| …to | ||||||
| Red | Yellow | Blue | Purple | Green | ||
| Red | 72% | 67% | 67% | 67% | ||
| Yellow | 58% | 58% | 67% | 67% | ||
| Path from… | Blue | 67% | 67% | 67% | 67% | |
| Purple | 69% | 69% | 67% | 72% | ||
| Green | 69% | 69% | 67% | 67% |
You can use this table to find a nice, sensible, and above all transitive order to put the dice in. The loser is the yellow die, because the path from it to any other die is weaker than the one in the opposite direction. Because there are only six sides on a die, there are some ties in this election, so depending on how the dice tumble, either the blue or purple die will win, since its path to any other die is stronger than the reverse path.
Arrow’s theorem still prevents it from being a perfect system. For example, it suffers from the same strange ‘vote punishing’ behaviour as AV, although mostly in strange electorates built from maths toys where there probably isn’t a right answer, which has to be better than a Parliament full of Condorcet losers.
Another quirk of beatpath is that if you’re a bit cheap and only buy the three-pack of Grime Dice, you still get a blue die, but the green one will beat it. It’s clear why this happens with a model electorate made out of dice — dice are only “good” or “bad” in comparison to other dice, and these ones are deliberately designed to make that comparison unintuitive. Potential MPs, on the other hand, can be rated in isolation, and while this won’t stop Condorcet’s Paradox arising from time to time, it does change things slightly: in theory, if you measure strength of feeling, rather than just ranks, you’re no longer beholden to Arrow’s theorem. A simple method is called “range voting”, where you mark each candidate out of ten, and whoever gets most points altogether wins. In our example, Labour would win simply because the red die has the most spots on it. The problem now is that this relies on voters honestly reporting mild preferences as such so that the vote counters can properly ignore them, and that simply isn’t going to happen.
In theory, then, Labour are best, followed by the Lib Dems. But as far as anyone can possibly tell from five-party ballot papers, the Conservatives and UKIP are most popular — and the system we actually use is even worse.
This is why we are doomed.

This post, as featured on BBC Material World 19/04/2012!