Last week, A001462 – Golomb’s sequence – booked its place in the final. In retaliation for last week’s palaver, this week Christian has picked all the sequences. Unfortunately, the British Summer is happening today so we’re failing a bit, intellectually.

With that in mind, it’s time for round 4 of…
Here are the rules: we’re judging each sequence on four axes: Aesthetics, Completeness, Explicability, and Novelty. We’re reviewing six sequences each week for four weeks, picking a winner from each. Then, we’ll pick one sequence from the ones we reviewed individually before this thing started, plus a wildcard. Finally, a single sequence will be crowned the Integest Sequence 2013!
A005430
Apéry numbers: $n \binom{2n}{n}$0, 2, 12, 60, 280, 1260, 5544, 24024, 102960, 437580, 1847560, 7759752, 32449872, 135207800, 561632400, 2326762800, 9617286240, 39671305740, 163352435400, 671560012200, 2756930576400, 11303415363240, 46290177201840, ...
Christian: We’re off to a good start: I’ve completely forgotten why I picked this sequence. We can both judge it as if it’s new to our eyes.
David: I was looking at Pascal’s triangle and you saw the name Apéry and looked it up.
Christian: Oh yes! We were looking at Pascal’s tetrahedron! But I have no idea what this has to do with that. The OEIS entry isn’t particularly enlightening either, though it does use the rather lovely phrase “aerated sequence”.
David: I’ll judge its Aesthetics purely on how it looks, without knowing anything about the maths. <David requested an unwitty comment about zeroes here>.
Christian: Oh-ho! What a joker! I, too, find the zeroes unsettling.
David: It’s because there are loads of factorials in it. We should stop reviewing things with factorials in. They might be big, but they’re definitely not clever.
Christian: So that’s a trouncing in Aesthetics then. Completeness? Since we don’t have another category for this to go in, I’ll mention now that the definition of the Apéry numbers on MathWorld is completely different. What do you think?
David: Factorials are hard to compute.
Christian: No they’re not! They’re elementary, my dear boy!
David: They probably take a long time to compute though, don’t they? Like, look at $10^{10^{100}}!$. Which is, Christian…?
Christian: Fine. So you want a low Completeness score, even though they’re really simply defined and not that hard to work out?
David: I’m just fixing the score to match my gut reaction, as usual.
Christian: Nothing I don’t do. Explicability? I have no idea where the definition comes from.
David: If this was the old days I’d say five, but for some reason Explicability now includes motivation, so I’ll say 1. Table it, CP! ($ = C \cdot P \cdot O \cdot N \cdot M \cdots$)
| Aesthetics | $\frac{1}{5}$ |
|---|---|
| Completeness | $\frac{3}{5}$ |
| Explicability | $\frac{1}{5}$ |
| Novelty | $\frac{4}{5}$ |
| TOTAL | $\frac{9}{20}$ |
Christian: <maniacal laugh>
A116260
$n (n+4)$ gives the concatenation of two numbers $m$ and $m-4$.9, 99, 999, 9999, 99999, 999999, 9999999, 99999999, 999999999, 9999999999, 36363636362, 45454545453, 54545454544, 63636363635, 72727272726, 81818181817, 90909090908, 99999999999, 999999999999, 9999999999999, ...
David: My head hurts. Explain with examples, mother effer.
David would like to apologise, and blames his behaviour on possible sunstroke.
Christian: $99 \times 103 = 10197$, which is the concatenation of $m = 101$ and $m-4 = 97$. But what I like about this sequence is the numbers that aren’t just strings of nines.
David: First of all, should it not be $a(n)$ instead of $n$ in the definition? Like ALL OTHER SEQUENCES. That’s what confused me so much. Bloody sausages. If they had a sensible definition I would have given it 5 across the board. Since I don’t like how they did it it’s all ones I’m afraid.
| Aesthetics | $\frac{1}{5}$ |
|---|---|
| Completeness | $\frac{1}{5}$ |
| Explicability | $\frac{1}{5}$ |
| Novelty | $\frac{1}{5}$ |
| TOTAL | $\frac{4}{20}$ |
David: Next.
Christian: Whoah! Slow your roll, Cushing. You’re acting impulsively. I think the juxtaposition of repetition and occasional free-jazz interludes has a lot going for it.
David: Fine. I’ve calmed down a bit. I’ve just licked an ice cube.
Christian: I think 4 for Aesthetics is fair.
David: There’s a lot of nines! It’s pretty funky. Like, there’s a lot that aren’t nines. I like it.
Christian: That’s what I’ve been saying all along.
David: Nevertheless, 0 for Explicability.
Christian: That’s a bit harsh. 2. Now, I’m not sure about Completeness. I think this is finite.
David: Really?
Christian: Yeah. Let $n = 10^k-1$. Then $(10^k-1)(10^k+3) = 10^{2k} + 2 \cdot 10^k – 3$, which is clearly the concatenation of $10^k+1$ and $10^k-3$.
David: YOU JUST SAID IT WAS FINITE!
Christian: I meant infinite. Do a Möbius transform and they’re the same thing. Maybe. Anyway, it’s infinite, but I don’t know if any more funky ones appear. I haven’t really thought about it. So, 4?
David: OK.
Christian: Finally, Novelty? I like it. It’s got a fresh new sound, and you can tap your feet to it.
David: I’ve seen some concatenations before. I’m pretty sure we reviewed one last week. So we should give this that one’s score minus 1. But I’m not looking it up, so… 3?
Christian: I’ve learned not to even try to argue with things like that.
| Aesthetics | $\frac{4}{5}$ |
|---|---|
| Completeness | $\frac{4}{5}$ |
| Explicability | $\frac{2}{5}$ |
| Novelty | $\frac{3}{5}$ |
| TOTAL | $\frac{13}{20}$ |
A146968
Brocard’s problem: positive integers $n$ such that $n!+1 = m^2$.4, 5, 7, ...
Christian: pffffffffft!
David: Christian! What have you done?
Christian: In case you’re wondering about the dots, a comment on the OEIS says there are no other known terms below $10^9$.
David: 
Christian: I hate its sneakiness. Only three terms? WHAT ARE YOU HIDING, A146968?
David: What’s the definition, again?
Christian: It’s $n$ such that $n!+1$ is a square.
David: I think I have a proof that shows there are only finitely many. Be right back.
<David starts writing abc conjecture nonsense on the blackboard.>
Christian: Nooooooooooope!
…
Christian: I don’t like this!
David: What don’t you like?
Christian: Until you can prove the abc conjecture to me using words of four letters or less, I won’t accept it.
David: If you assume the abc conjecture, it only has finitely many solutions.
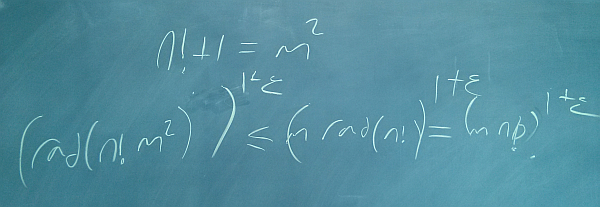
Christian: Well, you know what happens when you assume.
David: That Japanese guy proved it possibly.
Christian: Anyway. Infinitude aside, we need to assign some scores. Aesthetics: 1, because 4,5 and 7 happen to be my least favourite numbers.
David: Why?
Christian: Respectively, 4, 5 and 7 ninjas, cowboys and pirates killed my parents, grandparents, and dog. Ol’ Yeller was a real fighter.
David: I know we normally take away points if it’s finite or probably finite, but the proof to show it’s finite is pretty cool.
Christian: I don’t understand your proof or many of the letters used in it.
David: Completeness is 5. (If the abc conjecture is true. And if none of the other potential finite number of solutions have not been found yet)
Christian: That disclaimer alone is worth a two point penalty. Three.
David: It’s pretty damn Explicable. But, for Novelty, I’m getting sick of short sequences. It was fun at first, we laughed, we giggled, we were young. 1.
Christian: I’m happy with 1.
| Aesthetics | $\frac{1}{5}$ |
|---|---|
| Completeness | $\frac{3}{5}$ |
| Explicability | $\frac{5}{5}$ |
| Novelty | $\frac{1}{5}$ |
| TOTAL | $\frac{10}{20} =\frac{1}{2}$ |
David: That’s not thirteen, Christian!
Christian: I know. I’m as scared as you are.
David: Next sequence, I want a goodie. Blow my socks off. Or knock my socks off. Or blow my mind. Or any of the above.
A082274
Palindromes $k$ such that $k + 2$ is also a palindrome.1, 2, 3, 4, 5, 6, 7, 9, 99, 999, 9999, 99999, 999999, ...
David: Heehee!
Christian: I can explain this. You know I like palindromes, and you know I like twin primes, so I thought: why not put those two great tastes together? And, because everything is, it was already in the OEIS.
David: Are there any that aren’t just nines later on? Because I don’t think there are.
Christian: Funny you should say that, old chum. The only comment on the OEIS entry says,
Perhaps from 8th term onwards the only members are a(n) = 10^(n-7) – 1 for n > 7.
David: But what other numbers could there be? Surely it has to be all nines. Because we’re changing the last digit by adding 2, so the first digit has to be changed by adding 2.
Christian: I agree with you. We should add a comment to the OEIS saying the original author should be more firm in his convictions. So: scores?
David: I don’t really like the OEIS any more.
Christian: Yes, we can give this one low scores, but look at the bigger picture.
David: What bigger picture?
Christian: The one with a painting of your radical mood swings on it.
| Aesthetics | $\frac{2}{5}$ |
|---|---|
| Completeness | $\frac{5}{5}$ |
| Explicability | $\frac{5}{5}$ |
| Novelty | $\frac{1}{5}$ |
| TOTAL | $\frac{13}{20}$ |
A103456
$0^n+10^n-1$1, 9, 99, 999, 9999, 99999, 999999, 9999999, 99999999, 999999999, 9999999999, 99999999999, 999999999999, 9999999999999, 99999999999999, 999999999999999, 9999999999999999, 99999999999999999, 999999999999999999, ...
Christian: This sequence is stupid and its entry number is stupid.
David: Is this just all the 9s with a 1 at the front?
Christian: Yes it is. Consider it revenge for A051200.
David: Do you want me to seriously review this? This is the worst. Like, just, all… AAAGH!
Christian: I want to give a negative score for Aesthetics.
David: Minus… what?
Christian: –1 would do. And the other categories can all be zero, except maybe for Completeness.
David: Yeah, Completeness deserves quite a lot, unfortunately.
Christian: But it hardly uses any of the digits! It uses two of the possible ten digits, so $\frac{1}{5}$.
| Aesthetics | $\frac{-1}{5}$ |
|---|---|
| Completeness | $\frac{1}{5}$ |
| Explicability | $\frac{0}{5}$ |
| Novelty | $\frac{0}{5}$ |
| TOTAL | $\frac{0}{20}$ |
A023811
Largest metadrome (number with digits in strict ascending order) in base $n$.0, 1, 5, 27, 194, 1865, 22875, 342391, 6053444, 123456789, 2853116705, 73686780563, 2103299351334, 65751519677857, 2234152501943159, 81985529216486895, 3231407272993502984, 136146740744970718253, ...
David: What’s a metrodome?
Christian: Metadrome. Its a number whose digits are in strict ascending order. Other kinds of dromes include katadromes, plaindromes and nialpdromes. So, for $n = 3$, the biggest number with digits in strict ascending order is $(12)_3 = 3+2 = 5$, so $a(3) = 5$.
David: The problem is that we haven’t got them in base $n$, so I can’t see it. It’s a thing in a base and we’re not viewing it in that base. It’s like when you look at flowers. No offence.
Christian: But we could write this out in those bases. In fact I will, because it’s trivial.
1,12,123,1234,12345,123456,12346567,12345678,123456789,...
David: I want the next one.
Christian: 123456789A. Next question!
David: It’s a pretty cool idea. It doesn’t do much for me, though. It’s the sort of sequence I would come up with to try to get in the OEIS. That’s the only reason it’s in. Some man thought, “here’s a sequence that probably isn’t in the OEIS that’s pretty damn stupid. Let’s submit it anyway.”
Christian: If we had a Professional Ethics category it’d lose some marks there, but since we don’t it’s not going to factor in.
David: Should we score it on a whim instead of having a pointless discussion where we never agree? Should I get the dice out?
Christian: Let’s go with the whimsy.
| Aesthetics | $\frac{4}{5}$ |
|---|---|
| Completeness | $\frac{5}{5}$ |
| Explicability | $\frac{5}{5}$ |
| Novelty | $\frac{3}{5}$ |
| TOTAL | $\frac{17}{20}$ |
And the winner is…
A023811, the largest metadromes in base $n$!
A023811 advances to the final, having trounced some frankly puny competition, with an unexpectedly mighty score of $\frac{17}{20}$.
David: To be fair, even the winner’s pretty dire. Can we give it to the sequence you wouldn’t let me review, A075000?
Christian: Nope, it’s my week! Not even going to look at it.
David: I quit. I’m going to Sweden. Should we get some guest reviewers for the final?
Christian: Topping idea! Get on it.
David: A quick recap of who’ll be making it to the final:
- From Bracket 1: A002210, the decimal expansion of Khintchine’s constant.
- From Bracket 2: A001220, the Wieferich primes.
- From Bracket 3: A001462, Golomb’s sequence.
- From Bracket 4: A023811, the largest metadromes in base $n$.
- From the first round of reviews, we picked the one whose score we fiddled the least: A010727, all the 7s.
- And the wildcard is A058883, the wild numbers.
Christian: In fact, if you want to have a say in the competition, I’ve set up a form where you can vote for the Integest Sequence 2013. We’ll take a break from reviewing for a week, and announce the results in a celebrity maths gala on the 29th of July. Dress code: elbow patches!
A great set of reviews as ever! But in your explanation for A116260, $m=101$ not $103$. I wouldn’t normally be such a stickler about this, but I recently weaselled my way through a Maths degree and feel like this correction is putting those four years to good use.
Oh poo, I ruined the formatting of that.
Thanks to the magic of the editing system, you didn’t ruin the formatting and I didn’t make the original mistake.
(Thanks for pointing it out)
I don’t know if I must be proud to be the author of the winner sequence of this contest.
This was not exactly one of the few I would have picked to represent the OEIS in any circumstance.
While this sequence use the base _concept_ it is not really base dependent.
Anyway it is fun to read your sequence reviews.