Welcome to the Field of Dreams. Talking of which: why can’t you grow wheat in $\mathbb{Z}/6\mathbb{Z}$?
Anyway, we’re finally here: the Grand Finale of our tournament to find the Integest Sequence 2013. Here’s a reminder of the sequences vying for the title:
- From Bracket 1: A002210, the decimal expansion of Khintchine’s constant.
- From Bracket 2: A001220, the Wieferich primes.
- From Bracket 3: A001462, Golomb’s sequence.
- From Bracket 4: A023811, the largest metadromes in base $n$.
- From the first round of reviews, we picked the one whose score we fiddled the least: A010727, all the 7s.
- And the wildcard is A058883, the wild numbers.
It’s a been a long, hard battle. We’ve seen some good sequences, some bad sequences, and an awful lot of plagiarised GIFs. So, without further ado, it’s time to start the
CP: So, the final. How are you feeling, Dave?
David: Nervous. I think a lot of people are going to be angry with us by the end of this post.
CP: Why?
David: For starters, we’ve had over 500 entries in the public vote, and we haven’t looked at a single one.
CP: Should we get on that? Let’s get on that.
| Sequence | Votes |
|---|---|
| A002210, the decimal expansion of Khintchine’s constant. | 185 |
| A001220, the Wieferich primes. | 53 |
| A023811, the largest metadromes in base n. | 50 |
| A001462, Golomb’s sequence. | 231 |
| A010727, all the 7s. | 66 |
| A058883, the wild numbers. | 14 |
| Total | 599 |
David: I won’t have a chance of understanding that until you put it in a pie chart.
CP: Ahyup:
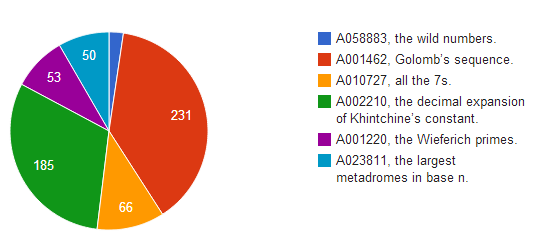
David: Well that’s a good win for the Wieferich primes in the first round.
CP: Your unique interpretation of otherwise incontrovertible facts is why you’re on the team. How did the Wieferich primes win the public vote?
David: Most votes per term. Wild numbers came second, with every other sequence dead last.
CP: Well, we didn’t declare a method before we started, so well done getting in there first.
David: Were any of the reasons for voting for particular sequences funny enough to type out?
CP: I’ll let you decide.
The public’s stupid reasons for voting for these stupid sequences
A002210, the decimal expansion of Khintchine’s constant.
Jonas F.: Although the constant itself is not an integer, it is achieved by expressing real numbers as a sequence of integers (continuous fraction), and that is what makes this number amazing and the integest. This constant may be useful for future applications in mathematics. At last: Wieferich, Golomb and metadromes are interesting, too.
Metagross31: It was just mindblowing! That is a really AWESOME constant. Furthermore the most other sequences are not so cool…
Om: Mind blow
Travis: Because it’s badass.
A001220, the Wieferich primes.
Charles R Greathouse IV: The Wieferich primes have many applications. For example, pseudoprimes are squarefree unless divisible by the square of a Wierfrich prime. They have many interesting properties: even though they seem to be rare, it has yet to be proved that there are infinitely many primes which are *not* Wieferich primes (though this is believed under certain hypotheses). They’re connected to many major problems like Fermat’s last theorem and the abc conjecture. They’re believed to be very sparse, doubly-logarithmic, so they’re special in that sense as well.
Ernst: The loneliest primes… perhaps some day they will have more siblings
HeiloKing: Primes are awesome!
Hunter: It’s short and sweet. I don’t think an infinite sequence could be called the integest!
Kevin Hine: There might only be two.
Miłosz: It seems pretty cool that those two apparently random 4-digit primes have actually something in common and that it actually has been spotted.
Stewart Feasby: Because it’s amazing how a pattern can be so small and that the only 2 terms found below $6.7 \times 10^{13}$ are 4 digits long. I can’t wait to see when it’s proven that there are an infinite amount of terms OR maybe only 2!
Anonymous: Only two primes in the sequence found so far?! That just blows my mind! :D
Nathan Barker (long-standing Aperiodichum):
There are only two known numbers in the sequence, but it is conjectured to be infinite! Hilarious.
Aesthetics: well, it looks good and 1092 = 444 (base 16) and 3510 = 6666 (base 8)!
Completeness: well, there are only two numbers……. but the possibility there are more is exciting!
Explicability: it is very easy to explain why these two numbers are special but it appears hard to find any more like them.
Novelty: since there are only two numbers in the sequence (so far!), it is fairly novel.
A058883, the wild numbers.
Joao Ferreira: Background history associated with the number. Otherwise Khinchine’s constant would be my favourite
Murica Jones: Because this is ‘Murica! Where we are WILD AND FREE!
A001462, Golomb’s sequence.
Greg: I mean, come on, it’s so beautifully meta and self-referential. Honourable mention though to the wild numbers which to me seem to be everything the OEIS stands for.
Joe Fu: Got to be Golomb: the integest surely must *count* something, and what better to count than itself?
Linus: Most of the other sequences aren’t very integ.
Khintchine’s constant: WHY, oh why, did you not pick your sequence to be the constant’s continued fraction expansion?? The decimal is both awkward (this isn’t an integer sequence, it’s a single real number) and also base-dependent, auigh!
Wieferich primes: Actually, these are okay. But a heuristic argument shows there are probably infinitely many Weiferich primes, so it’s a shame we only know two of them.
Metadromes: There is a trivial formula for the nth term, namely $(n^n-n^2+n-1)/(n-1)^2$. (To see why, try multiplying 123456789 by 9 and then by 9 again.)
All the 7’s: Again, there is a trivial formula for the nth term; namely, $\cosh(2n i \pi + 4 \operatorname{atanh}((\sqrt{5}+1)/2))-2$. Also what is this sequence doing here
Wild numbers: I didn’t like the book very much. Nyah.
Paige: IT’S JUST COOL IT MAKES SO MUCH SENSE AND JUST IT’S FAB U KNOW
Rich P: Almost self aware, the sequence perpetuates itself as how many times a particular number appears becomes determined as though by fate. Also it contains ascending integers and as the sequence continues it’s funny to imagine ridiculous repetitions of ridiculously large numbers. This is why it is the integest sequence.
Solomon W. Golomb (really? – CP): Me > All
Zhaggy: Everytime phi = golden ratio comes out of something I get excited.
J C McKeown: Because known nontrivial fixedpoints beat conjectural fixedpoints. that’s why.
A023811, the largest metadromes in base $n$.
Chris H: Suprisingly BASE-ic.
Daniel Herkes: Base $n$ says it all.
Falcon: Base math is the best math.
gckbowers411: The most interesting thing about it is how you have these numbers that have unforeseeable properties when you use them as the base of a number system. For example, who would have thought that 2 would correspond to 5 (which is a completely unrelated number), while 3 gets it’s own cube, 27? I’m sure there are more patterns deep within this sequence that could be found.
Jackson L.: Because it’s math, but it’s fun math! I was torn between this one and Golomb’s sequence.
Gregory Foote: I am very fond of base number counting systems and this sequence neatly condenses the bases of number counting systems
A010727, all the 7s.
7: 7
7: 7777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777
<a few more votes in a similar vein>
The Waffle Man: Because waffles are delicious.
Nathalie: SEVEN
Andrew Kevin Walker: What’s in the box?!?!?!?!?
Joris: Because it’s silly.
Theo: It reminds me of the part in ViHart’s twelve tone video where she plays the same note on a piano repeatedly.
W.: Why not?
David (not that David): It contains the most important sevens.
pinna_be: for the use of “all the” when there is actually only 1
Max: Math strives for simplicity, and All the 7s fulfills that.
The Waffle Man: Waffles really ARE delicious.
CP: The Waffle Man really did vote twice, and I thank him for that. And for transparency, here’s the full list of votes.
David: Are we done then?
CP: No, we’ve still got to pick a winner.
David: And we still need to use the celebrity reviews.
CP: “Celebrity”? Oh, those people we emailed. Yes. Some of them replied!
Get these guys with their opinions and their book deals
David Spiegelhalter
Winton Professor of the Public Understanding of Risk; fellow of Churchill College, Cambridge; author of The Norm Chronicles; Winter Wipeout contestant.
Sorry, don’t think I can give a valid vote as I cannot understand any of the sequences…
CP: We’re not off to a good start here.
David: At least he replied!
Steve Mould
Part-time database administrator; part-time science presenter; a third of a herd of nerds.
I enjoyed finding out about Khintchine’s constant, so tempted to vote for that. But it’s the decimal expansion, which to me, is not that interesting, it’s just a result of the way we write numbers. The metadromes are out for the same reason. Though it has some merit because it’s ABOUT the way we write numbers as opposed to just a consequence of it. Wieferich primes I like because you can get to the end. I like all the 7 because, you know, 7. The wild numbers are like a double rainbow (“what does it mean?!”). But for me the winner is Golomb’s sequence because it’s about itself and I like self referential things. The fibonacci sequence refers itself, but it only refers to elements of the sequence that have already occurred. The Golomb’s sequence refers to elements that WILL occur later on. Brilliant!
Steve votes for: Golomb’s sequence!
Richard Elwes
Author, mathematics lecturer, blogger.
A002210, the decimal expansion of Khintchine’s constant.
As a piece of mathematics, this is one of the lesser known gems. If this was a “Mathematical Constant Review Mêlée Hyper-Battle DX 2000”, I’d be backing Khintchine all the way. But how much of this magic comes through in the sequence? To my mind, not all that much. Also – to be borne in mind below – it entirely hinges on the decimal system, which is a cultural artifact rather than a mathematical one.
A001220, the Wieferich primes.
Yes, very interesting – I’d not come across these before, and will certainly borrow them for the next time I teach number theory. It would have been even more interesting before we knew the solution to Fermat’s Last Theorem! I’m not really sure why this should get the nod over the better known Mersenne or Fermat primes. It’s good, but doesn’t feel like a gold medalist.
A001462, Golomb’s sequence.
Yes, very nice. Very nice.
A023811, the largest metadromes in base n.
Another good one. Nice to have the decimal hegemony broken, with base n represented in the nth position.
A010727, all the 7s.
Just 7s eh…. what am I missing? A spectacularly tedious sequence to my mind.
A058883, the wild numbers.
Again, I’m going to need a hand here. The OEIS says “Apparently these are completely fictional and there is no mathematical explanation.” If so, nul points.
So, in the absence of further evidence to be supplied in favour of A010727 or A058883, it comes down to Golomb versus the Metadromes (which sounds like a TV show I’d watch). I should admit that neither of these sequences has really deep mathematics underlying it, unlike say A001034. But both are hugely satisfying as integer sequences. Judged in these terms, Golomb’s sequence is both more mysterious and (paradoxically) easier to grasp. Both have interesting limiting properties, with $\frac{m(n)}{m(n-1)} – \frac{m(n-1)}{m(n-2)}$ tending to $e$ and $g(n)$ asymptotically equal to $\phi^{2-\phi} n^{\phi-1}$. The latter of these strikes me as both neater and more unexpected. So, I go for Golomb.
Richard votes for: Golomb’s sequence!
David: Uh oh. Is this going to be one-sided?
CP: Do you mean a one horse race?
David: … Maybe. Do you think any of these people are going to read this article?
CP: Some less likely than others.
David: So we can make them say what we want?
CP: Let’s change the next guy’s thing.
Jacob Aron
Physical sciences reporter for New Scientist.
I’ve been a big fan of
the OEISChristian and David ever since I first discovereditthem, which has got to beat least a decade agothe defining moment of my life, so I’m happy to help you pick a winner. I will slightly cheat first though by suggesting my own sequence, A053169, “A paradoxical sequence: a positive integer $n$ is in this sequence if and only if $n$ is not in sequence $A_n$ in the database.” Russell fans can see where this is going. As for your list of sequences, it has to be A010727. Just like 6, we should all be in eternal fear and awe of 7, for as you know, 789…
Jacob votes for: All the 7s!
CP: He didn’t pick Golomb, so I changed a different bit instead.
David: Next up we have friend of the show, and long-time reader, Thomas Andrew Fisher.
Tom Fisher
PhD student at Newcastle University. Not to be trifled with. He’s for reals.
Many thanks for your e-mail. I would be very happy to contribute.
My favourite
None of these are my favourite. They are all in joint last place. Sorry guys!
Comments
A002210: I like this one because it is so unexpected that it should be independent of the real number chosen.
A001220: I like this one because the abc-conjecture is nice. But I don’t like that there are only two known numbers in the sequence.
A001462: I like this one because it is very interesting and I like self-referential sequences that don’t lead to paradoxes (the last time I wrote down a paradox, my page caught fire).
A023811: I like this one because it starts with 0, 1, and then you might expect it to continue with 2, 3, 4, …, but then it surprises you. That’s all I have to say about this sequence, which is otherwise, in my opinion, quite contrived.
A010727: I like this one because even though I know what every term is, maybe it’ll be different next time.
A058883: I like this one because of its name, and the fact that the fifth term is equal to the second term, I guess. Otherwise it’s really, really stupid.
Technically speaking, Tom
CP: Only technically speaking?! What’s his real name? Anyway, he didn’t pick a winner. Total walloon.
David: What’s a walloon?
CP: Tom’s one.
David Roberts
Mathematician at the University of Adelaide, category theorist, probably overqualified for this judging panel.
My pick for the integest sequence: A001220
Why? Consists of primes; presently the shortest possible length for a sequence (arguably one could have empty or length-one sequences, but probably not in OEIS), but expected to be infinite; and some of the best conjectures about this (as mentioned on the OEIS) involve the abc conjecture, and don’t even answer the question about the length of the sequence!
David votes for: the Wieferich primes!
Patrick Honner
Award-winning New York maths teacher, exam board haranguer.
A001462, Golomb’s Sequence. It was mostly process-of-elimination. I didn’t care much for the others.
But I like the fact that (a) all integers will appear in this sequence, and (b) in a way the integers are considered both as individual objects and as a system in the formulation of this sequence, which I think bolsters it’s claim to be the integest.
James Grime
Enigmatic guy; YouTube sensation; one of your five portions of singing fruit and veg a day.
How did Khintchine’s constant get in here? While it may be an awesome constant I cannot vote for it as the most Integest Sequence. It would be like a Hungarian dance group winning Britain’s Got Talent. Three Xs from me. If this was Constant Idol – no problem.
Golomb’s Sequence, at least this is an actual sequence, but it’s a bit cutesy for me. Like one of those sequences you get in puzzle books where the letters represent the months of the year, or some nonsense. Hey Golomb, here’s a self-referential sequence for you, it goes: 1, 2, 3, 4, 5, 6, 7, 8, 9… I’ve got a formula for that too.
Largest metadromes base n, pretty patterns in different bases? Jog on.
All the 7s is a sequence that constantly surprises. It’s starts off with 7, then it’s 7, then 7, 7, 7, 7 – and just when you think they’re not possibly going to hit you with another 7 – BOOM! 7. It’s the sequence M. Night Shyamalan would have written.
Wild Numbers is a sequence of integers that, when you repeatedly apply a number of simple operations to the integer, returns another integer. It is also ficticious. I think I like this way of doing maths. So, with this in mind, and after much research, I can now announce my latest breakthrough in mathematics. I have discovered a new number. I have decided to call it twenteen. Fields Medal please!
I love Fermat’s Little Theorem – and so should you. Internet encryption, and our whole modern, world depends on this 400 year old fact, that every prime divides $x^p – x$ (for all $x$). We should all bow down to it, and its cousin the Wieferich primes. It’s also connected to Fermat’s Last Theorem and the abc Conjecture – this sequence is hanging around with some important stuff. The fact that it is incomplete is only a bonus to me – a good sequence should be like a beautiful woman, mysterious and divides $2^{p-1} – 1$. This sequence represents the best of mathematics while reminding us that our work is not yet complete, and promising more to come! And so, that is why the Wieferich Primes are my choice for the Integest Sequence.
James votes for: the Wieferich primes!
Alex Bellos
Journalist, blogger for The Guardian and author of Alex’s Adventures in Numberland / Here’s Looking at Euclid.
Golomb’s sequence, without question. I’m attracted to self reference, as I like to say about myself, and also to mathematicians – like Solomon Golomb – whose full name uses only one vowel. I ruled out all the other sequences because either they were too complicated, or had no element of mathematical surprise. I think it really cool the way that Golomb’s sequence is such a simple idea, and produces a sequence that ascends so subtly. That it also links to the golden ratio is the icing on the cake.
Alex votes for: Golomb’s sequence!
CP: That’s the end of the celebrity reviews, and the end of the competition. We don’t have any more information to consider, do we?
David: Nope.
CP: Since both the public and celebrity votes agreed, I think the contest is over.
David: Golomb’s sequence is our winner! Should we get it a trophy?
CP: Like, a real trophy?
David: Yeah, we can get all of the winning sequence’s terms engraved on it.
<time passes>
CP: … OK, I asked the trophy guy, and the only sequence we can fit on the plaque is the Wieferich primes.
David: CONGRATULATIONS TO THE WIEFERICH PRIMES, THE INTEGEST SEQUENCE 2013!
CP: Wahey! Finally, some silverware in Newcastle!

CP: So, we started a contest as a joke, it got a bit out of hand, we appeared on Numberphile and received over 500 votes from the public and esteemed public intellectuals, all of which we ignored, and to top it all off we bought a ridiculous trophy for the undeserving winner.
David: And more, much more than this.. WE DID IT OUR WAY
[youtube url=http://www.youtube.com/watch?v=8e0_q9aecb0]
Final thoughts
David: I don’t think there is a best sequence.
CP: They’re all special?
David: No, there’s quite a lot of shit ones. But there’s quite a few sequences close to my heart (pi for one) which I could never choose between.
CP: Well put. If this has shown us anything, it’s that –
David: – if you run a beauty contest, an uggo is going to win.
CP: Umm, quite. As a closing remark, Matt McIrvin brought to my attention the fact that there are uncountably many integer sequences, but the OEIS uses the natural numbers as indices. So it can’t possibly be an encyclopedia! THIS WHOLE THING WAS A SHAM.
David: I’m never reviewing a sequence again.
CP: Me neither.
David: … Actually, I quite liked it.
CP: OK, then listen; let’s not stop reviewing integer sequences.
David: What’re you talkin’ about?
CP: Let’s keep goin’!
David: What d’you mean?
CP: Go.
David: You sure?
CP: Yeah.

David’s heading off to a conference in Sweden and will be taking a few weeks off maths after that, to recover his energies. CP hopes to be a fireman one day.
Integer sequence reviews will return, in
Coming to a blog near you, Autumn 2013.
(Huge thanks to the over 600 of you who took the time to vote. You know which sequence really won.)
2 Responses to “Integer Sequence Review Mêlée Hyper-Battle DX 2000, THE GRAND FINALE”