Since you’re here reading this, you probably know that on October 30th, Matt “Friend of the Site” Parker released his book, Things to Make and Do in the Fourth Dimension. If you’ve gone one further and read it, you might have seen the occasional reference to the website, makeanddo4d.com. If that website is the book’s DVD extras, this is the website’s extras. We’re going to peek behind the scenes and see how it all works. (Spoiler alert: the maths is powered by maths. It’s recursive maths, all the way down.)
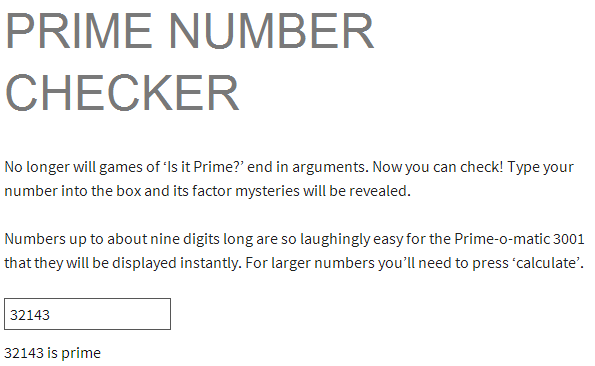
Let’s start with the Prime Number Checker. It’s a text box that tells you the prime factors of any number (integer greater than one) you type into it. The guts of the source code is in this file on GitHub, and there are two things I like in there. First, the same thing can be done in a single line of code:
for (var p=[], m=2; n>1; m++) for (; !(n%m); n/=m) p.push(m);
You should not do it that way. (If you must, you should at least space it onto three lines.)
The second thing I like is that the entire algorithm is in there twice, and the reason is fairly interesting. Matt’s book mentions binary, and how computers encode numbers, and that’s sort of why I needed two versions of this algorithm. The first uses actual numbers, stored in binary inside the computer and processed as such by the CPU. That works really well up to about nine million billion, after which there are no prime numbers. Since we know there are actually an infinite number of them (and have found some) clearly something’s gone wrong.
The problem is that Javascript stores numbers of that size as ‘floating point’ numbers – essentially scientific notation in binary. A number might be stored as $1.00101101 \times 2^{10011011}$. After nine million billion, it runs out of digits in the main part of the number and has to start increasing the exponent instead. This works great for almost every conceivable purpose, except of course that any number in that form divides by $2$.
In Python that’s no problem because it will happily deal with infinite strings of binary numbers, but the pleasingly absurd Javascript solution is Big.js, a complete rewrite of numbers, which allocates as much memory as it needs and can in principle store any size number exactly, with all its prime factors intact. (In practice, of course, it uses regular numbers to index the array and would therefore conk out somewhere below ten-to-the-nine-million-billion.)
The most complex of the various toys and gadgets, because I got a little carried away, is the Polygonal Number Calculator. This will take a number and tell you if it is (say) a triangle number, a hexagon number, or a prime — and it will demonstrate this fact by arranging the dots into a triangle or a hexagon. The source is split across a few files, but most of the maths is in the property checker and the dance generator.
There’s some tricky hidden maths in here. For example, I wanted to make sure that nearby dots would usually be different colours, no matter what shape I arranged them in.
If you read the chapter about turning a photo into a spreadsheet, you know computers show colours as red, green and blue dots. If you’re read any other sentence at all of the book, you’ll probably be comfortable thinking of those as three dimensions of a cube, where a colour is simply a point within the cube. If we don’t mind spinning and bending that cube, we can use any 3D coordinate system we want to describe a colour. We can even jump into polar coordinates and think of colour as a cylinder, with the rainbow around the circumference (with red and blue joined up by magenta, largely to annoy Steve Mould). To generate the dot colours, I just move around that circular rainbow by a set angle each time.
But what angle? $90°$ would repeat after four dots, which is plainly no good. In fact, any rational number would repeat eventually. And any number near a rational isn’t ideal – $\pi$ is irrational, but $360\pi°$ would make roughly $22$ rotations after $7$ dots and nearly repeat. We need the most irrational number there is and, insofar as such a thing exists, the best candidate is $\phi$.
I set the dots to each be $360\phi°$ further around the hue wheel than the last (or maybe I used $\frac{360°}{\phi}$ – I can’t remember, and the weird thing about $\phi$ is that it doesn’t matter) and the result is that apart from some funky stripes around Fibonacci numbers, the dots largely behave and you don’t notice much structure to them.
There’s also a bonus gadget just for you guys, which lets you play with the angle and see if you can find a nicer arrangement of colours. You can choose an angle step, and then highlight every $p$ dot to see if you can see clear lines, which will appear as stripes and blocks in our dot patterns. The hue wheel with $\phi$ as the angle step creates a familiar sunflower image, and by setting $p$ to Fibonacci numbers you can see the seed spirals, which map exactly to the stripes we saw earlier. I never understood before making this why the spirals came in Fibonacci numbers, but now I do: if every $13$th seed makes a spiral, then there must be $13$ such spirals – increase the $i$ spinner to see them all.
Speaking of Fibonacci dot patterns, the Fibonacci numbers are represented by the classic Fibonacci spiral, but to be honest this is slightly a fudge: the number of dots is essentially the total length of the spiral, but normally you start with no spiral and add each Fibonacci term as you go, which is elegant and beautiful, but not what we want.
| $n$ | $n$th Fibonacci number | Length of spiral |
|---|---|---|
| 1 | 1 | 1 |
| 2 | 1 | 2 |
| 3 | 2 | 4 |
| 4 | 3 | 7 |
| 5 | 5 | 12 |
None of those spiral lengths are Fibonacci numbers, although they are all one less than a Fibonacci number. I genuinely don’t know if that pattern will continue forever. Luckily, the differences between them all are Fibonacci numbers – obviously – and the difference between two Fibonacci numbers is also a Fibonacci number: $F_n = F_{n-1} + F_{n-2}$, so $F_n – F_{n-1} = (F_{n-1} + F_{n-2}) – F_{n-1} = F_{n-2}$, which is sort-of obvious too. All I need to do is to fudge the start of the spiral so that adding the $n-2$th Fibonacci number will give us $F_n$ dots. That fudge turns out to be squeezing in an extra dot before the spiral kicks in, which means that the pattern in our table earlier does continue forever. Hey, we learned something together: $\sum_{i=1}^{n} F_i = F_{n+2}-1$.
There’s also a little light geometry that went into working out how far apart dots could be in each pattern, and the fact that the whole thing runs on computers which are basically maths with keyboards, but I think I’ve already gone on too long, so I will leave you to play with the remaining gadgets (including a deleted scene that didn’t make the book) and peek at the source code.


Andrew,
I have just stumbled onto your work via Matt Parker’s Things to Make And Do in the 4th D site. Your work is all very impressive and great fun.
I would love to send some photo-spreadsheet conversion files to fellow Excel abusers, but I cannot use Matt’s because his site is not secure. Is there any other way that you can recommend that I can do this conversion?
Thanks so much,
Scott