It’s been almost two years since I last sat down with my friend David Cushing and did what God put us on this Earth to do: review integer sequences.

This week I lured David into my office with promises of tasty food and showed him some sequences I’d found. Thanks to (and also in spite of) my Windows 10 laptop, the whole thing was recorded for your enjoyment. Here it is:

I can only apologise for the terrible quality of the video – I was only planning on using it as a reminder when I did a write-up, but once we’d finished I decided to just upload it to YouTube and be done with it.

We reviewed the following sequences:

A075771
Let $n^2 = q \times \operatorname{prime}(n) + r$ with $0 \leq r \lt \operatorname{prime}(n)$; then $a(n) = q + r$.

1, 2, 5, 4, 5, 12, 17, 10, 15, 16, 31, 36, 9, 28, 41, 48, 57, 24, 31, 50, 9, 16, 37, 48, 49, 76, 15, 42, 85, 116, 79, 114, 137, 52, 41, 96, 121, 148, 27, 52, 79, 144, 139, 16, 65, 136, 109, 84, 141, 220, 49, 86, 169, 166, 209, 254, 33, 124, 169, 240, 55, 48, 297, 66

A032799
Numbers $n$ such that $n$ equals the sum of its digits raised to the consecutive powers $(1,2,3,\ldots)$

0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 89, 135, 175, 518, 598, 1306, 1676, 2427, 2646798, 12157692622039623539

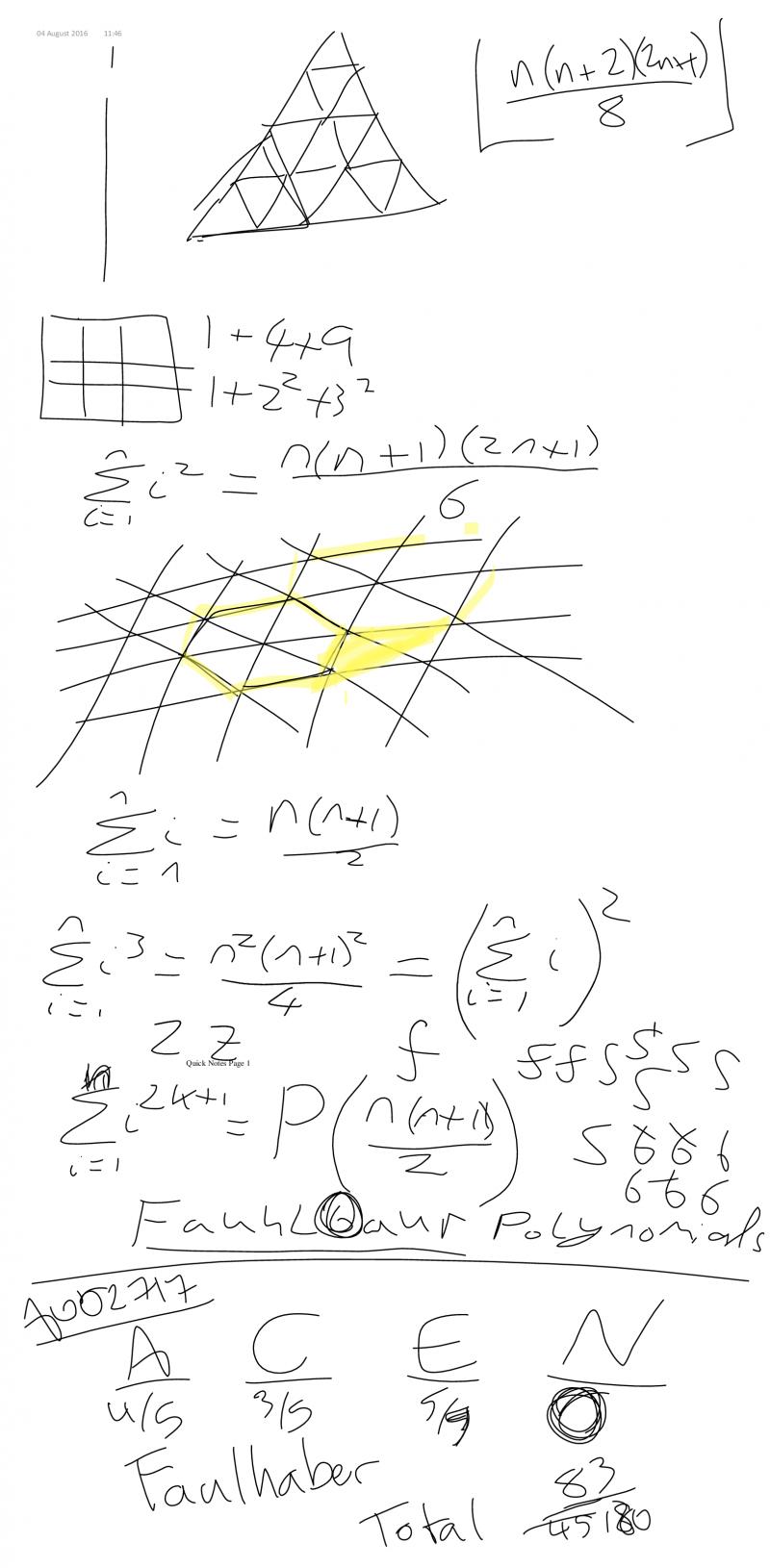
A002717
$\lfloor n(n+2)(2n+1)/8 \rfloor$

0, 1, 5, 13, 27, 48, 78, 118, 170, 235, 315, 411, 525, 658, 812, 988, 1188, 1413, 1665, 1945, 2255, 2596, 2970, 3378, 3822, 4303, 4823, 5383, 5985, 6630, 7320, 8056, 8840, 9673, 10557, 11493, 12483, 13528, 14630, 15790, 17010, 18291, 19635, 21043, 22517