One would be hard put to find a set of whole numbers with a more fascinating history and more elegant properties surrounded by greater depths of mystery — and more totally useless — than the perfect numbers.

— Martin Gardner

There are countless ways to classify integers. Happy, perfect, friendly, sociable, abundant, extravagant, cute, interesting, frugal, deficient, hungry, undulating, weird, vampire… the list goes on. But how useful are such classifications, beyond their inherent interestingness, and as a hook to get people into number theory?

A small team from the maths department at the University of Manchester has become involved with several Puzzle Hunts, which are large-scale puzzle competitions involving word-based, logic and number puzzles, with themes ranging from Alice in Wonderland to Pokemon, and quite often run by maths departments at other universities around the world including Sydney, Melbourne and MIT.

One puzzle, from the 2010 Melbourne Puzzle Hunt, which quite nicely illustrated one such flippant class of numbers, was as follows. Those presented with the puzzle were directed to a website consisting of an implementation of a mind reading trick. Having been asked to choose a number between 0 and 31, you are presented with a series of five cards, covered in a selection of numbers, on each of which your number will or will not be present. The website allows you to click a button to say YES or NO, and in response shows you a different card. After five cards, the website tells you what your original number was. This is the extent of the information you’re given to solve the puzzle, and is typical of the type of thing you get in such puzzle hunts.

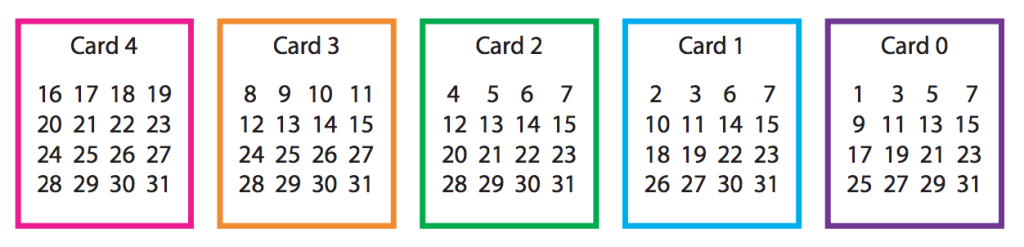
The well-known version of this game, described here, uses the five cards shown above, and the numbers 1 to 31. The layout here is such that the presence or absence of a number corresponds to a 1 or 0 in its binary expansion in that position. This set of cards may be used for ‘mind-reading’ on the spot, and is employed frequently by the team at Maths Busking (as well as probably hundreds of teachers in a quest to instruct students about binary numbers, and the manufacturers of Christmas crackers). The same method is extended to larger numbers in this Mystery Calculator. However, the cards presented to us by the puzzle were different.

After repeated playing of the game from start to finish, we established that the card layouts, while the numbers on them were randomly rearranged each time the card is presented, were drawn from a set of five cards, as shown below.

The same method as for the binary cards, where digits are 1 and 0 if the number is present or absent, applied to some of the cards – for example, the leftmost card consists of numbers whose binary expansion contains a 1 in the $2^2$ position. However, the rule for the second card from the left was not immediately obvious. (If you’d like to try to solve the puzzle, stop reading here and go and solve it.)

It turns out that the numbers on the second card, when put into the OEIS, are all Evil numbers. This is one of the many subsets which have been defined without recourse to their usefulness – although in this case, there are several nice applications of this particular set of numbers – but it wasn’t necessarily the highest priority of the person who named them. Even so, I found it quite neat that Evil numbers are those which have an even number of 1s in their binary expansion. This gives someone who knows the other four digits, as in our game above, the ability to establish the identity of the number, by a parity argument. It amused me even more to discover that the other set of numbers, those with an odd number of 1s in their binary expansion, are termed Odious numbers.

The solution to the puzzle took us a little longer, as sometimes it’s hard to see a simple solution to a problem when you’ve delved beyond to the deeper levels. The standard binary trick can be performed by children, if you explain to them that you have to add together the smallest number on each card the person states their number is present on, which will be exactly the powers of two. For the puzzle’s set of cards, the presence of your number on a card means you add a certain number and take the result modulo 32, then add 25 (mod 32) to get the final answer. When these numbers are converted to letters of the alphabet, they spell out TROPHY. A full explanation is given here.

For more information about Puzzle Hunts, here are some recommended examples: Melbourne University, Sydney University, CISRA (Canon Australia), MIT, and Intercoastal Altercations. There is also a Puzzle Hunt Calendar, detailing when different hunts take place.