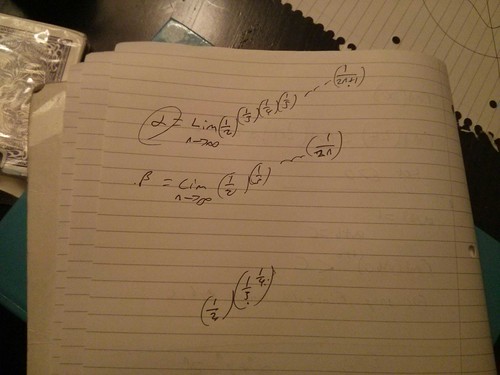Well! I have been quite remiss in writing up the Newcastle MathsJams. The last recap published was for May’s meeting. The end of the year (and associated holiday) is a good time to kick myself up the backside and do the entire second half of the year in one go. So, here’s that.
June
It turned out John also has a copy of Is Maths Inevitable?. It’s a good book!
I have written down this question:
How many sets of Mad Abel rules are there for decks of 52 cards?
And then I’ve written down a reference to OEIS sequence A000001, the number of groups of order $n$.
Some teachers from the RGS came to ask if they could send their students. They were a little bit rude! (For reference, the answer was: “we’re sitting in a pub.”)
I brought in some books I’d bought from Barter Books. They were: MATHEMATICS, which has some lovely colour plates; Practical Geometry and Graphics; and an unloved book of logarithms which has had an unfinished flickbook animation of a train drawn in it.
The best magic-ish square of all time!
I asked if there are more people with the title ‘Professor’ than ‘Sir’. I quickly added in Dames to the right-hand side, but it was a losing battle from the start. We reckon there are way more Professors than members of the Order of the British Empire of any sort.
I then asked how many different things there are on sale in the UK priced less than 5p, and whether I have enough money to buy one of each. I haven’t written down our answers, but thinking about it now I reckon I could do it.
Next, we talked about Australian Aboriginal kinship rules. They’re fascinating! We worked out a few of the possible permutations of intermarriages, and saw that they do a pretty good job of preventing inbreeding if you stick to them.
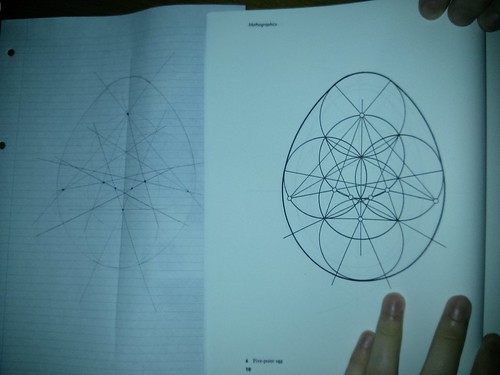
We looked at the book Mathographics, which Edmund Harriss recommended to me.
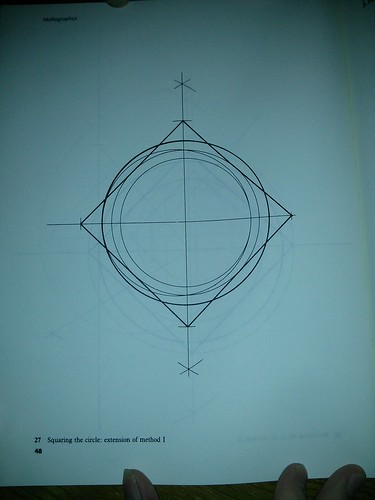
Here’s a dubious method from Mathographics:
Is my battered old Rubik’s cube deliberately set up with the pattern of a Conway’s Life glider in this photo?
Here’s a puzzle:
Write the numbers 1 to 14 around a circle so that the sum and difference of every pair of adjacent numbers is prime.
And here’s a solution:
1 – 12 – 5 – 2 – 9 – 14 – 3 – 8 – 11 – 6 – 13 – 10 – 7 – 4 – …
We played Mastermind with the other MathsJams over Twitter. It was a bit of a mess. I got one of my answers wrong, which confused everybody.
I might have mentioned my obsession with interesting times before. We realised that there’s a good stretch of really interesting numbers between 12:33 and 12:37.
- 12:33 $12^2 + 33^2 = 1233$ (mentioned months ago)
- 12:34 yes.
- 12:35 Fibonacci sequence
- 12:36 $1+2+3 = 6$; $1 \times 2 \times 3 = 6$; $12 \mid 36$. (best time)
- 12:37 $1,2,3,7$ are the first four Heegner numbers, as well as the first four record trajectory lengths for the Collatz problem.
If you can extend the happy moment in either direction with an interesting fact about 12:32 or 12:38, please tell me.
John said that Gauss invented the fast Fourier transform two years before Fourier invented the Fourier transform.
We drew a five point egg (page 10 of Mathographics).
We tried to work out the best deal for a second-hand maths book, prompted by the fact I bought MATHEMATICS for £1.80 and my lovely 1811 arithmetic textbook for £5. We decided you should try to maximise
\[ \frac{\text{Goodness}}{\text{Price}} \left( \times \text{ age} \right) \text ? \]
We agreed that the best possible deal would be an original Euclid parchment for 1p.
June was a busy month!
July
John has Khinchin’s book!
Context: David and I reviewed Khinchin’s constant as part of the Integer Sequence Review Mêlée Hyper-Battle DX 2000 and we thought it was the best (disregard the subsequent rounds of the competition).
A puzzle:
I talked about the Matula-Goebel bijection between natural numbers and rooted trees.
We did puzzles 22 and 100 from Mathematical Quickies by the excellently-named Charles Trigg.
I brought in my Buckyballs again. I made everyone angry by insisting on arranging them into a cube before leaving, and failing repeatedly.
John said that $n!$ can always be written as the sum of $n$ distinct divisors of $n!$.
A final puzzle:
Write down the numbers $1$ to $n$. Remove a number. The mean of the remaining numbers is $20 \frac{1}{3}$. What’s $n$?
Leeds tweeted that $n = 40$, and you take away $27$.
August
I missed August. I was tired from having a nice time in Wales. Sorry!
September
There were loads of us in September! Good ol’ back to school times.
Mike showed us his blue and red relativity graphs. The idea is that you see a time-distance graph from different reference frames by wearing different pairs of colour-filter glasses.
Eamonn brought in his MiQube, and a wooden magic square.
We did puzzle 260 from Mathematical Quickies.
David asked what sets of numbers $A$ have the property that $\lvert A + A \rvert = 2 \lvert A \rvert$. He’s since expanded this thought into a ruddy great paper with lots of mentions of Terence Tao.
John asked:
What’s the lowest possible degree of a regular graph of diameter 12?
I tried to instigate some Mad Abel, but people weren’t feeling it.
We reckon that Cantor’s tartan (link goes to some slides; I couldn’t find a good reference) is the solution to the Simon the snake problem if he only bends at right angles. (I think. I should take better notes.)
We talked about the Wieferich primes, which went on to be crowned Integest Sequence 2013.
I have written down “spiral cake”. Maybe I was planning on making one. That didn’t happen.
I showed everyone pictures of the art I commissioned from Edmund Harriss for Newcastle Uni’s maths building.
David showed us a limit that makes no sense:
\[ \frac{1}{2}^{\,\frac{1}{3}^{\,\frac{1}{4}^{\,\dots}}} \]
I mentioned the toast formula.
We played a few games of Set.
Mike posed this problem:
I have a biased coin. $\Pr(\text{heads})$ was picked at random from $U(0,1)$ when it was made. I toss it twice. What’s the probability of the second toss being heads, given that the first toss came up heads?
Here’s a game:
Draw $n$ vertices on the plane. Players take turns to draw an edge. The first to complete a triangle loses.
I’ve written down that on six vertices, we reckoned that the first player loses.
How many magmas are there of order $n$? I have a feeling that a couple of people looked this up later, but I can’t remember what the answer was.
October
John 3D-printed the Herschel enneahedron!
It’s very nice to hold. When I held it in my hand, the thought occurred to me that you could use it as a die. I asked what probabilities the different faces would have. We realised that there’s a way of constructing the enneahedron so that each face had the same probability of landing facing downwards, but our proof was non-constructive.
I’ve written down “Herschel graph – Stiglitz”. Any ideas what that means, anybody?
The MathsJam twitter account passed $\lfloor 1000 \pi \rfloor$ tweets.
Mike showed us his “magic” coins. They were: 1 HH, 1 TT, 4 TH. Apparently they give the closest approximation to a uniform 50-50 distribution of faces of any bag of mixed coins, if you take one out at random and toss it.
Mike also showed us The Fractionator:
We talked about searching for things in $\pi$. We decided it was too hard.
It was Martin Gardner’s 99th anniversary, or close to it. Most people present didn’t know very much about him.
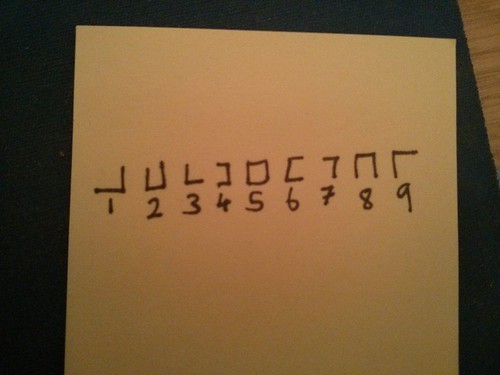
Here’s a code:
What’s going on?
I brainstormed ideas for the MathsJam conference cake-baking contest. I decided to attempt a series of cakes each containing a mix of brown and white sponge, so that any random slice would have a 50% chance of having purely white edges. The most fiddly solution would’ve required baking a circular Cantor set.
November
The last Newcastle MathsJam of 2013! Unlike some of the other MathsJams, we’re not hardcore enough to meet on Christmas Eve, and too stubborn to reschedule to the week before.
I had thought about my enneahedron-as-a-fair-die idea. I decided I needed to get some money to 3D-print a load of different-sized enneahedra to find the one closest to a fair die.
I’ve written down “Zina’s shape thing”. That’s a reference to David’s supervisor, who has described a 3D shape mathematically but has no idea what it looks like, and wants to 3D print it to find out.
A puzzle, from Stephen?
Arrange seven points in the plane such that there are exactly three lines with exactly two points on them.
Much drawing of Fano planes and so on ensued. Stephen (or whoever) then asked for thirteen points and six lines with exactly two points on each. Then we found out about the Sylvester-Gallai theorem.
We decided we’d like to make a mug with the heat equation printed on the side in thermal ink so it only appears when the mug is hot.
A puzzle from one of the other MathsJams:
Wrap a 1×1×1 cube with a 3×3 square of paper.
We found the really easy solution where you place the cube diagonally in the middle of the paper, before finding out that the puzzle insisted you can only fold on grid-lines, and cutting is allowed. We found that solution too, so we’re still clever.
Which is best plane? John said the projective plane, Stephen voted for the complex plane, and I was shouted down when I promoted the sphere.
Pick a sequence of moves on the Rubik’s cube. What’s its period? (The number of repetitions needed to get back to the solved state)
91 is the smallest number that passes the easy divisibility tests but isn’t prime. (This was a tweet from another MathsJam, or another mathematician, I think.)
It looks like that’s everything I’ve written down at MathsJam since May. See you in January!
By the way, previous MathsJam recaps have been published at my old mathem-o-blog. I decided I preferred The Aperiodical’s layout so I’ll be publishing them here from now on.